new work updates (#42)
Browse files- update (8c6ef6419a54b83e9e8e1d896d5a76af9c7db003)
- assets/images/tp_diagram4.png +2 -2
- dist/assets/images/tp_diagram4.png +2 -2
- dist/index.html +57 -49
- src/index.html +57 -49
assets/images/tp_diagram4.png
CHANGED
|
Git LFS Details
|
|
Git LFS Details
|
dist/assets/images/tp_diagram4.png
CHANGED
|
Git LFS Details
|

|
Git LFS Details
|
dist/index.html
CHANGED
|
@@ -983,25 +983,33 @@
|
|
| 983 |
|
| 984 |
<p>To come up with a strategy to follow, let’s move from a toy example to a real model building block. A Transformer model is made of two main building blocks : Feedforward layers (MLP) and Multi-Head Attention (MHA). We can apply tensor parallelism to both.</p>
|
| 985 |
|
| 986 |
-
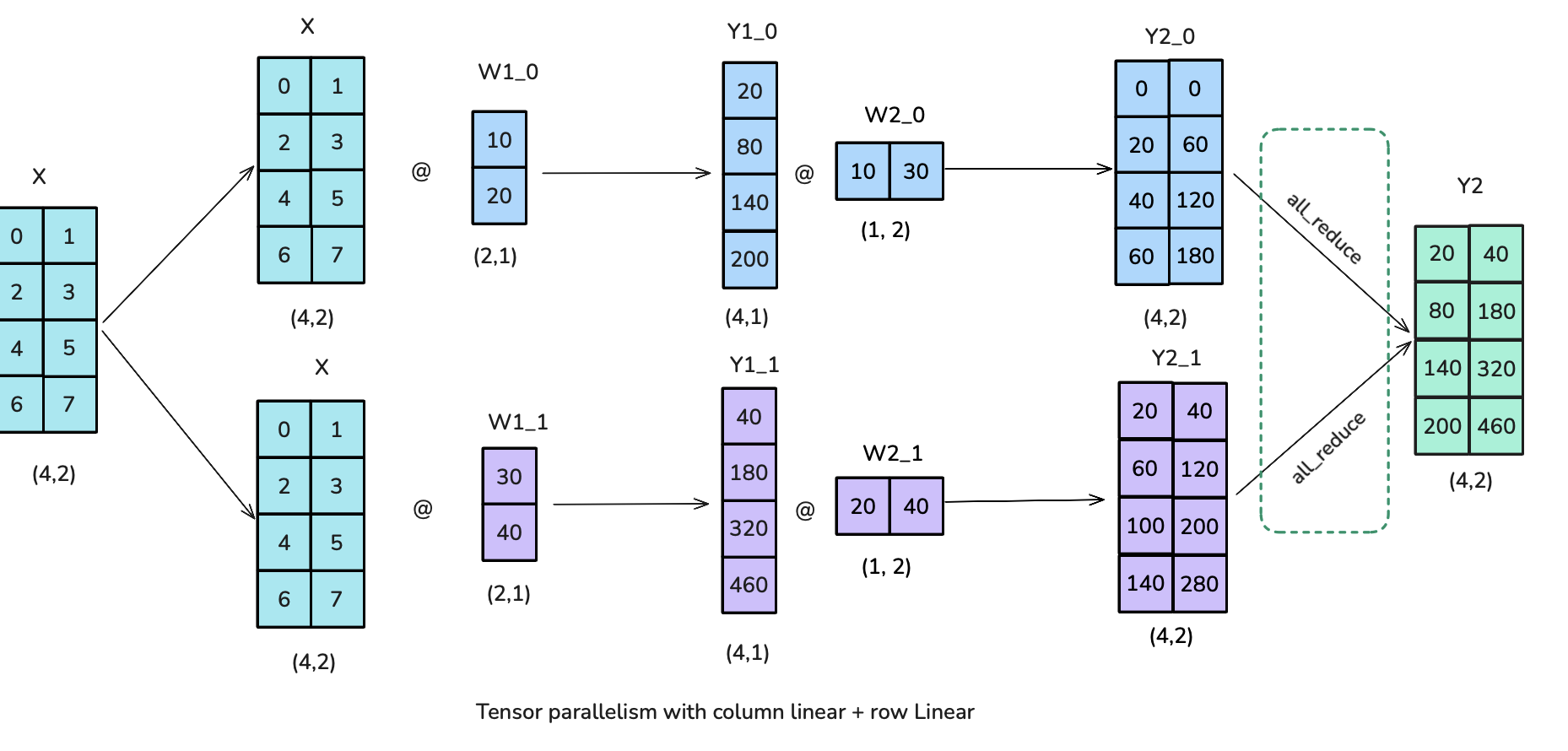
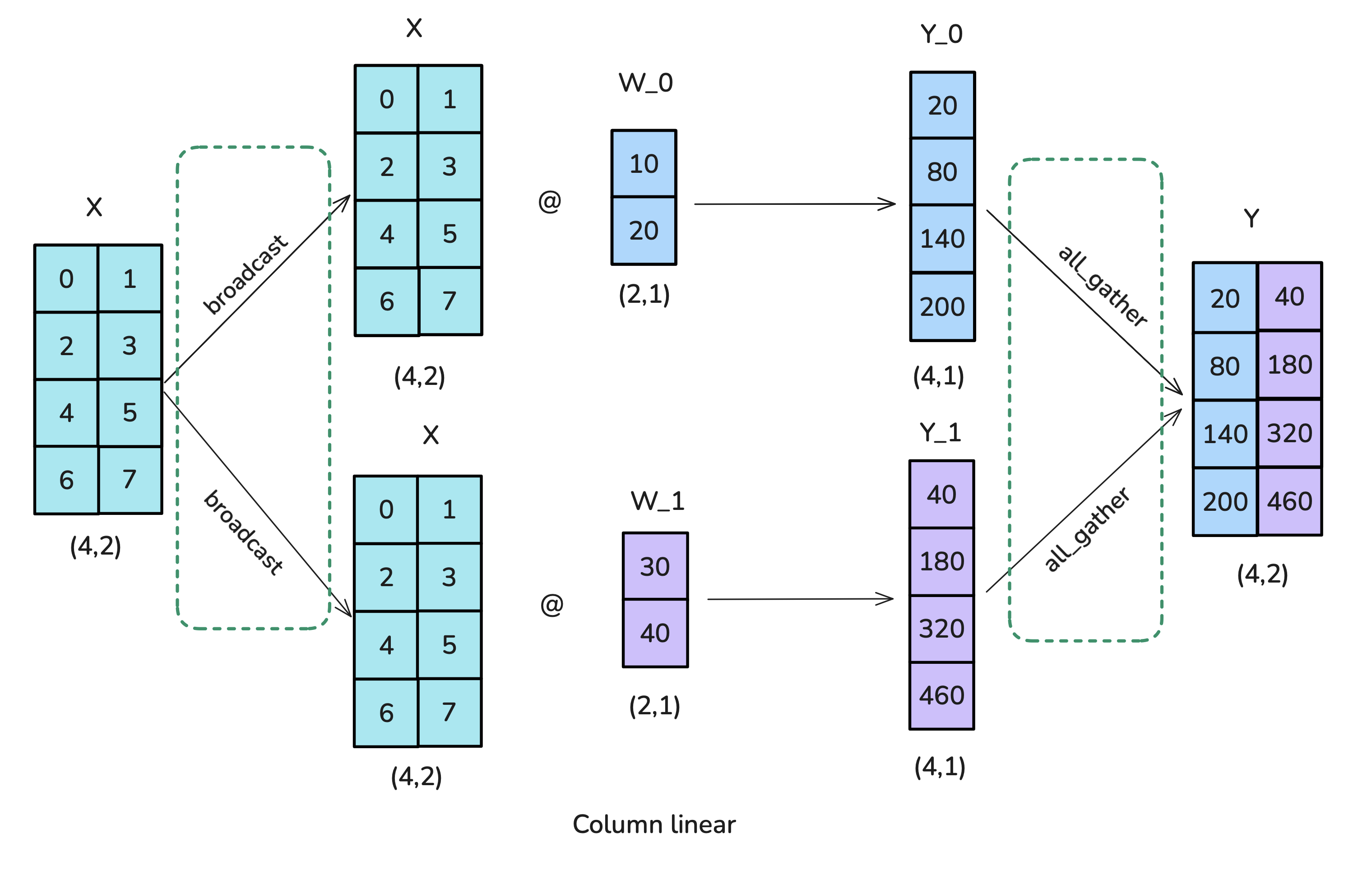
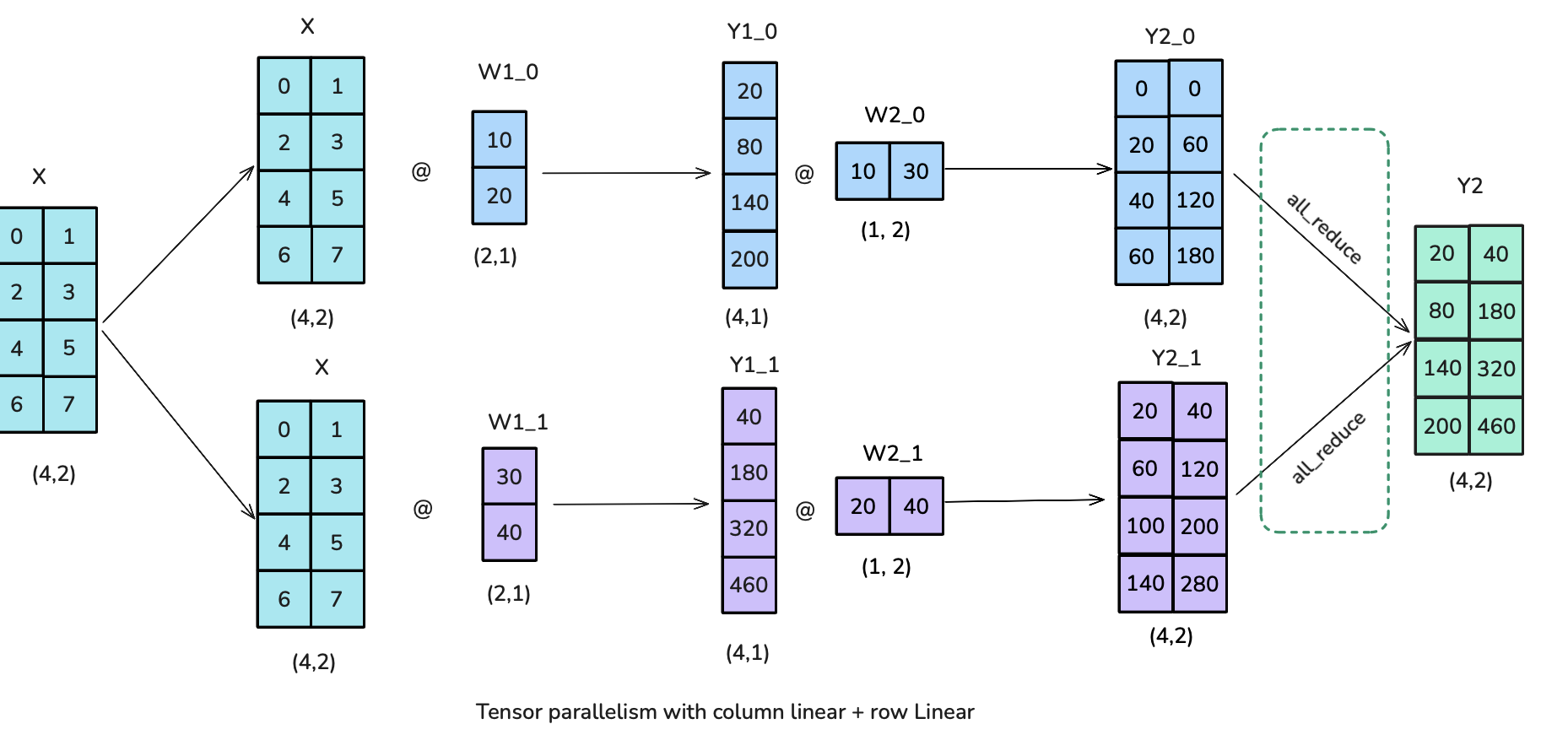
<p>The Feedforward part can be parallelized by having a “Column linear” followed by a “Row Linear” which amounts to a broadcast to copy the input and an all-reduce in forward. Note that the broadcast isn’t needed in actual training where we can make sure inputs are already synced across TP ranks.</p>
|
| 987 |
|
| 988 |
<p><img alt="image.png" src="/assets/images/tp_diagram4.png" /></p>
|
| 989 |
|
| 990 |
-
<p>Now that we’ve found
|
| 991 |
|
| 992 |
<p>We can generally follow a similar approach where Q, K, and V matrices are split in a column-parallel fashion, and the output projection is split along the row dimension. With multi-head attention, the column-parallel approach has a very natural interpretation: each worker computes the attention for an individual or a subset of heads. The same approach works as well for <a href="https://arxiv.org/abs/1911.02150"><strong><em>multi-query</em></strong> (MQA)</a> or <a href="https://arxiv.org/abs/2305.13245"><strong><em>grouped query attention</em></strong> (GQA)</a> where key and values are shared between queries. </p>
|
| 993 |
|
| 994 |
-
<p>It's
|
| 995 |
|
| 996 |
<p><img alt="image.png" src="/assets/images/tp_full_diagram.png" /></p>
|
| 997 |
|
| 998 |
-
<p>Finally note that
|
| 999 |
|
| 1000 |
<p><img alt="Forward pass in Tensor Parallelism" src="/assets/images/tp_overlap.svg" /></p>
|
| 1001 |
|
|
|
|
|
|
|
| 1002 |
<p>Looking at the timeline of operations in tensor-parallel MLP (same applies for Attention), we can better understand the tradeoffs involved. In the forward of each decoder layer, we hit a synchronization point with the AllReduce operation that cannot be overlapped with computation. This <em>exposed communication</em> overhead is necessary to combine partial results across tensor-parallel ranks before the final LayerNorm can be applied. </p>
|
| 1003 |
|
| 1004 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1005 |
|
| 1006 |
<iframe class="l-body-outset" id="plotFrame13" src="assets/data/benchmarks/tp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1007 |
<script>
|
|
@@ -1014,11 +1022,11 @@
|
|
| 1014 |
<!--
|
| 1015 |
<p><img alt="Impact of Tensor Parallelism on model performance and batch size capacity: while increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training." src="/assets/images/tp_scaling.svg" /></p> -->
|
| 1016 |
|
| 1017 |
-
<p>
|
| 1018 |
|
| 1019 |
-
<p>In practice, the communication overhead of tensor parallelism becomes particularly noticeable as we scale beyond 8 GPUs. While tensor parallelism within a single node can leverage fast NVLink interconnects, going across nodes requires slower network connections.
|
| 1020 |
|
| 1021 |
-
<p>
|
| 1022 |
|
| 1023 |
<iframe class="l-body-outset" id="plotFrame7" src="assets/data/benchmarks/tp_memoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1024 |
<script>
|
|
@@ -1030,7 +1038,9 @@
|
|
| 1030 |
</script>
|
| 1031 |
<!-- <p><img alt="tp_memoryusage.svg" src="/assets/images/tp_memoryusage.svg" /></p> -->
|
| 1032 |
|
| 1033 |
-
<p>
|
|
|
|
|
|
|
| 1034 |
|
| 1035 |
<div class="note-box">
|
| 1036 |
<p class="note-box-title">📝 Note</p>
|
|
@@ -1039,24 +1049,22 @@
|
|
| 1039 |
</div>
|
| 1040 |
</div>
|
| 1041 |
|
| 1042 |
-
<p>
|
| 1043 |
|
| 1044 |
<h3>Sequence Parallelism</h3>
|
| 1045 |
|
| 1046 |
-
<p>
|
| 1047 |
-
|
| 1048 |
-
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 1049 |
-
|
| 1050 |
<div class="note-box">
|
| 1051 |
-
|
| 1052 |
-
|
| 1053 |
-
|
| 1054 |
-
|
| 1055 |
-
|
| 1056 |
|
| 1057 |
-
|
| 1058 |
-
|
| 1059 |
-
|
| 1060 |
\text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta
|
| 1061 |
</d-math>
|
| 1062 |
|
|
@@ -1070,7 +1078,7 @@
|
|
| 1070 |
in backward: f = all-reduce ; f* = no-op ; g = reduce-scatter ; g* = all-gather
|
| 1071 |
SP region needs full hidden_dim" src="/assets/images/tp_sp_diagram.png" /></p>
|
| 1072 |
|
| 1073 |
-
<p>in forward: f = no-op ; f<em> = all-reduce ; g = all-gather ; g</em> = reduce-scatter in backward: f = all-reduce ; f<em> = no-op ; g = reduce-scatter ; g</em> = all-gather SP region needs full hidden_dim</p>
|
| 1074 |
|
| 1075 |
<p>The diagram shows how we transition between tensor-parallel and sequence-parallel regions using different collective operations (labeled "f" and "g"). The key challenge is managing these transitions efficiently while keeping memory usage low and maintaining correctness.</p>
|
| 1076 |
|
|
@@ -1194,19 +1202,17 @@
|
|
| 1194 |
</script>
|
| 1195 |
<!-- <p><img alt="tp_sp_memoryusage.svg" src="/assets/images/tp_sp_memoryusage.svg" /></p> -->
|
| 1196 |
|
| 1197 |
-
<p>
|
|
|
|
|
|
|
| 1198 |
|
| 1199 |
<p>If you’ve been paying close attention, you’ll notice that we’re talking about 4 comms ops in each layer (2 for Attention and 2 for MLP). This is how the MLP profiling looks like when using Tensor + Sequence Parallelism:</p>
|
| 1200 |
|
| 1201 |
<p><img alt="tp_sp_overlap.svg" src="/assets/images/tp_sp_overlap.svg" /></p>
|
| 1202 |
|
| 1203 |
-
<p>
|
| 1204 |
-
|
| 1205 |
|
| 1206 |
-
<
|
| 1207 |
-
|
| 1208 |
-
<p>As you might expect, this communication overhead becomes increasingly problematic as we scale up tensor parallelism. To illustrate this, let’s check throughput as we scale TP with SP for a 3B model:</p>
|
| 1209 |
-
<aside> For example, Megatron-LM/Nanotron implement a partial overlapping of all-gather with FC1 computation, and we expect to see more innovations in this space as the field continues to evolve.</aside>
|
| 1210 |
|
| 1211 |
<iframe class="l-body-outset" id="plotFrame2" src="assets/data/benchmarks/tp_sp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1212 |
<script>
|
|
@@ -1218,7 +1224,7 @@
|
|
| 1218 |
</script>
|
| 1219 |
|
| 1220 |
<!-- <p><img alt="tp_sp_scaling.svg" src="/assets/images/tp_sp_scaling.svg" /></p> -->
|
| 1221 |
-
<p>
|
| 1222 |
|
| 1223 |
<p>Let’s summarize our observations:</p>
|
| 1224 |
|
|
@@ -1233,7 +1239,7 @@
|
|
| 1233 |
<div class="note-box">
|
| 1234 |
<p class="note-box-title">📝 Note</p>
|
| 1235 |
<div class="note-box-content">
|
| 1236 |
-
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to all-reduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is a small communication overhead since LayerNorm has relatively few parameters.</p>
|
| 1237 |
</div>
|
| 1238 |
</div>
|
| 1239 |
|
|
@@ -1243,9 +1249,9 @@
|
|
| 1243 |
|
| 1244 |
<h2>Context Parallelism</h2>
|
| 1245 |
|
| 1246 |
-
<p>With Tensor Parallelism and Sequence Parallelism, we can reduce the memory requirements per GPU significantly as both model weights and activations are distributed across GPUs. However, when training models on longer and longer sequences (e.g. when scaling to 128k or more tokens per sequence) we might still exceed the memory available on a single node
|
| 1247 |
|
| 1248 |
-
<p>
|
| 1249 |
|
| 1250 |
<iframe class="l-body-outset" id="plotFrame9" src="assets/data/benchmarks/cp_8Bmemoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1251 |
<script>
|
|
@@ -1258,19 +1264,17 @@
|
|
| 1258 |
|
| 1259 |
<!-- <p><img alt="image.png" src="/assets/images/cp_memoryusage.svg" /></p> -->
|
| 1260 |
|
| 1261 |
-
<p>
|
| 1262 |
-
|
| 1263 |
-
<p>
|
| 1264 |
-
|
| 1265 |
-
<p>The idea of Context Parallelism is quite simple; just like Sequence Parallelism, we’ll split the input along the sequence dimension but we now apply this splitting along the full model, instead of only the sequence parallel regions of the model as we’ve done previous with Tensor + Sequence Parallelism.</p>
|
| 1266 |
|
| 1267 |
<!-- <p><img alt="cp_8Bmemoryusage.svg" src="/assets/images/cp_8Bmemoryusage.svg" /></p>
|
| 1268 |
-->
|
| 1269 |
<p>Splitting the sequence doesn't affect most modules like MLP and LayerNorm, where each token is processed independently. It also doesn’t require expensive communication like TP, as only the inputs are split and not the weight matrices. Just like data parallelism, after computing the gradients, an all-reduce operation is initiated to synchronize the gradients across the context parallelism group.</p>
|
| 1270 |
|
| 1271 |
-
<p>There is one important exception though
|
| 1272 |
|
| 1273 |
-
<p>Because Context Parallelism splits the inputs along the sequence dimension across GPUs, the attention module requires full communication between GPUs to exchange the necessary key/value data.</p>
|
| 1274 |
|
| 1275 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1276 |
|
|
@@ -1283,23 +1287,25 @@
|
|
| 1283 |
|
| 1284 |
<h3>Discovering Ring Attention</h3>
|
| 1285 |
|
| 1286 |
-
<p>In this implementation of attention, each GPU first initiates
|
| 1287 |
|
| 1288 |
-
<p>
|
| 1289 |
|
| 1290 |
<ol>
|
| 1291 |
-
<li>Send “current keys and values” to the next machine except during the last time step in a non-blocking manner so
|
| 1292 |
-
<li>
|
| 1293 |
-
<li>Wait to receive keys and values from the previous GPU and then
|
| 1294 |
</ol>
|
| 1295 |
|
|
|
|
|
|
|
| 1296 |
<p>The whole process with 4 GPUs is shown in the following animation:</p>
|
| 1297 |
|
| 1298 |
<p><img alt="ring-attention.gif" src="/assets/images/ring-attention.gif" /></p>
|
| 1299 |
|
| 1300 |
-
<p>
|
| 1301 |
|
| 1302 |
-
<p>There is one big problem though which is that a naive implementation of Ring Attention lead to some strong imbalance between GPU
|
| 1303 |
|
| 1304 |
<p><img alt="cp_attnmask.svg" src="/assets/images/cp_attnmask.svg" /></p>
|
| 1305 |
|
|
@@ -1340,7 +1346,9 @@
|
|
| 1340 |
|
| 1341 |
<p>The All-to-All approach generally offers better memory efficiency at the cost of slightly more complex communication patterns, while the AllGather approach is simpler but requires more temporary memory during the attention computation.</p>
|
| 1342 |
|
| 1343 |
-
<p>We've now seen how we can split a model across one node with TP to tame large models and that we can use CP to tame the activation explosion with long sequences
|
|
|
|
|
|
|
| 1344 |
|
| 1345 |
<h2>Pipeline Parallelism</h2>
|
| 1346 |
|
|
|
|
| 983 |
|
| 984 |
<p>To come up with a strategy to follow, let’s move from a toy example to a real model building block. A Transformer model is made of two main building blocks : Feedforward layers (MLP) and Multi-Head Attention (MHA). We can apply tensor parallelism to both.</p>
|
| 985 |
|
| 986 |
+
<p>The Feedforward part can be parallelized by having a “Column linear” followed by a “Row Linear” which amounts to a broadcast to copy the input and an all-reduce in forward. Note that the broadcast isn’t needed in actual training where we can make sure inputs are already synced across TP ranks. This setup is more efficient than starting with "Row Linear" followed by "Column Linear" as we can skip the intermediate all-reduce between both splitted operations.</p>
|
| 987 |
|
| 988 |
<p><img alt="image.png" src="/assets/images/tp_diagram4.png" /></p>
|
| 989 |
|
| 990 |
+
<p>Now that we’ve found an efficient schema for the Feedforward part of the transformer, let’s take a look at the multi-head attention block (MHA).</p>
|
| 991 |
|
| 992 |
<p>We can generally follow a similar approach where Q, K, and V matrices are split in a column-parallel fashion, and the output projection is split along the row dimension. With multi-head attention, the column-parallel approach has a very natural interpretation: each worker computes the attention for an individual or a subset of heads. The same approach works as well for <a href="https://arxiv.org/abs/1911.02150"><strong><em>multi-query</em></strong> (MQA)</a> or <a href="https://arxiv.org/abs/2305.13245"><strong><em>grouped query attention</em></strong> (GQA)</a> where key and values are shared between queries. </p>
|
| 993 |
|
| 994 |
+
<p>It's worth noting however that the tensor parallelism degree should not exceed the number of Q/K/V heads because we need intact heads per TP rank (otherwise we cannot compute the attentions independently on each GPU and we'll need additional communication operations). In case we’re using GQA, the TP degree should actually be smaller than the number of K/V heads. For instance, LLaMA-3 8B has 8 Key/Value heads, so the tensor parallelism degree should advantageously not exceed 8. If we use TP=16 for this model, we will need to duplicate the K/V heads on each GPU and make sure they stay in sync.</p>
|
| 995 |
|
| 996 |
<p><img alt="image.png" src="/assets/images/tp_full_diagram.png" /></p>
|
| 997 |
|
| 998 |
+
<p>Finally note that Tensor Parallelsim is still not a silver bullet for training. We’ve added several distributed communication primitive directly in the computation path of our model which are therefore hard to fully hide/overlap with computation (like we did in ZeRO), our final performances will be the results of a tradeoff between the computation and memory gains and the added communication overhead. Let's illustrate this:</p>
|
| 999 |
|
| 1000 |
<p><img alt="Forward pass in Tensor Parallelism" src="/assets/images/tp_overlap.svg" /></p>
|
| 1001 |
|
| 1002 |
+
<aside>It's possible to partially hide this communication by performing block matrix multiplication coupled with async communication/computation.</aside>
|
| 1003 |
+
|
| 1004 |
<p>Looking at the timeline of operations in tensor-parallel MLP (same applies for Attention), we can better understand the tradeoffs involved. In the forward of each decoder layer, we hit a synchronization point with the AllReduce operation that cannot be overlapped with computation. This <em>exposed communication</em> overhead is necessary to combine partial results across tensor-parallel ranks before the final LayerNorm can be applied. </p>
|
| 1005 |
|
| 1006 |
+
<aside>For example, Megatron-LM/Nanotron implement a partial overlapping of all-gather with FC1 computation where a portion of the matrix multiplication result will start to be sent to the other GPU while the other part is still being computed.</aside>
|
| 1007 |
+
|
| 1008 |
+
<p>Tensor parallelism does help reduce activation memory for the matrix multiplications since the intermediate activations are sharded across GPUs. However, we still need to gather the full activations for operations like LayerNorm, which means we're not getting the full memory benefits we could. Additionally, TP introduces significant communication requirements that heavily depend on the network infrastructure. The inability to fully hide this particular AllReduce behind computation means it directly adds to the critical path of forward propagation.</p>
|
| 1009 |
+
|
| 1010 |
+
<aside>This area of research is still an active area of research, with recent work like Domino <d-cite bibtex-key="wang2024domino"></d-cite> exploring novel techniques to maximize this overlap. </aside>
|
| 1011 |
+
|
| 1012 |
+
<p> Let's take a better look at the trade-off as we scale the TP degree:</p>
|
| 1013 |
|
| 1014 |
<iframe class="l-body-outset" id="plotFrame13" src="assets/data/benchmarks/tp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1015 |
<script>
|
|
|
|
| 1022 |
<!--
|
| 1023 |
<p><img alt="Impact of Tensor Parallelism on model performance and batch size capacity: while increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training." src="/assets/images/tp_scaling.svg" /></p> -->
|
| 1024 |
|
| 1025 |
+
<p>While increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training.</p>
|
| 1026 |
|
| 1027 |
+
<p>In practice and as we see above on the left plot, the communication overhead of tensor parallelism becomes particularly noticeable as we scale beyond 8 GPUs. While tensor parallelism within a single node can leverage fast NVLink interconnects, going across nodes requires slower network connections. We observe significant drops when moving from TP=8 to TP=16, and an even steeper decline from TP=16 to TP=32. At higher degrees of parallelism, the communication overhead becomes so high that it quickly dominates the computation time.</p>
|
| 1028 |
|
| 1029 |
+
<p>This being said, tensor parallelism provides important benefits for memory usage by distributing model parameters, gradients, optimizer states and activations (to some extent) across GPUs. Let's examine this effect on a 70B parameter model:</p>
|
| 1030 |
|
| 1031 |
<iframe class="l-body-outset" id="plotFrame7" src="assets/data/benchmarks/tp_memoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1032 |
<script>
|
|
|
|
| 1038 |
</script>
|
| 1039 |
<!-- <p><img alt="tp_memoryusage.svg" src="/assets/images/tp_memoryusage.svg" /></p> -->
|
| 1040 |
|
| 1041 |
+
<p>Increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU to the point where we can start fitting a large model on a single node of 8 GPUs. </p>
|
| 1042 |
+
|
| 1043 |
+
<p>Is there a way to get even more benefits from this technique? We've seen that layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 1044 |
|
| 1045 |
<div class="note-box">
|
| 1046 |
<p class="note-box-title">📝 Note</p>
|
|
|
|
| 1049 |
</div>
|
| 1050 |
</div>
|
| 1051 |
|
| 1052 |
+
<p>Let's explore next a small and natural extension to tensor parallelism, called <strong>Sequence Parallelism</strong> which does exactly that.</p>
|
| 1053 |
|
| 1054 |
<h3>Sequence Parallelism</h3>
|
| 1055 |
|
| 1056 |
+
<p><strong>Sequence parallelism (SP)</strong> involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension.</p>
|
| 1057 |
+
|
|
|
|
|
|
|
| 1058 |
<div class="note-box">
|
| 1059 |
+
<p class="note-box-title">📝 Note</p>
|
| 1060 |
+
<div class="note-box-content">
|
| 1061 |
+
<p>The term Sequence Parallelism is a bit overloaded: the Sequence Parallelism in this section is tightly coupled to Tensor Parallelism and applies to dropout and layer norm operation. However, when we will move to longer sequences the attention computation will become a bottleneck, which calls for techniques such as Ring-Attention, which are sometimes also called <em>Sequence Parallelism</em> but we’ll refer to them as <em>Context Parallelism</em> to differentiate the two approaches. So each time you see sequence parallelism, remember that it is used together with tensor parallelism (in contrast to context parallelism, which can be used independently).</p>
|
| 1062 |
+
</div>
|
| 1063 |
+
</div>
|
| 1064 |
|
| 1065 |
+
<p>This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 1066 |
+
|
| 1067 |
+
<d-math block>
|
| 1068 |
\text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta
|
| 1069 |
</d-math>
|
| 1070 |
|
|
|
|
| 1078 |
in backward: f = all-reduce ; f* = no-op ; g = reduce-scatter ; g* = all-gather
|
| 1079 |
SP region needs full hidden_dim" src="/assets/images/tp_sp_diagram.png" /></p>
|
| 1080 |
|
| 1081 |
+
<p>Where the abbreviations are: in forward: f = no-op ; f<em> = all-reduce ; g = all-gather ; g</em> = reduce-scatter in backward: f = all-reduce ; f<em> = no-op ; g = reduce-scatter ; g</em> = all-gather SP region needs full hidden_dim</p>
|
| 1082 |
|
| 1083 |
<p>The diagram shows how we transition between tensor-parallel and sequence-parallel regions using different collective operations (labeled "f" and "g"). The key challenge is managing these transitions efficiently while keeping memory usage low and maintaining correctness.</p>
|
| 1084 |
|
|
|
|
| 1202 |
</script>
|
| 1203 |
<!-- <p><img alt="tp_sp_memoryusage.svg" src="/assets/images/tp_sp_memoryusage.svg" /></p> -->
|
| 1204 |
|
| 1205 |
+
<p>As we can see, we've again strongly reduced the maximum memory usage per GPU, allowing us to fit sequence lengths of 16k tokens with TP/SP=16, an improvement over the vanilla TP case! (TP=16 is still a bit large as we've seen in the previous section, but we'll see how we can improve this in the next section).</p>
|
| 1206 |
+
|
| 1207 |
+
<p>One question you may be asking yourself is whether using TP+SP incurs more communication than vanilla TP? Well, yes and no. In the forward pass of a vanilla TP we had two all-reduce per transformer block, and in SP we have two all-gather and two reduce-scatter per transformer block. So SP does twice the number of communication operations as TP. But since an all-reduce operation can be broken down into to an all-gather + reduce-scatter (see the <a target="_self" href="#a_quick_focus_on_ring_allreduce" class="">A quick focus on Ring AllReduce</a> section in the appendix) they’re actually equivalent in terms of communication. Same reasoning for backward as we just use the conjugate of each operation (no-op ↔ allreduce and allgather ↔ reducescatter).</p>
|
| 1208 |
|
| 1209 |
<p>If you’ve been paying close attention, you’ll notice that we’re talking about 4 comms ops in each layer (2 for Attention and 2 for MLP). This is how the MLP profiling looks like when using Tensor + Sequence Parallelism:</p>
|
| 1210 |
|
| 1211 |
<p><img alt="tp_sp_overlap.svg" src="/assets/images/tp_sp_overlap.svg" /></p>
|
| 1212 |
|
| 1213 |
+
<p>Just like vanilla TP, TP+SP can’t easily be overlapped with compute, which makes throughput heavily dependent on the communication bandwidth. Here again, like vanilla TO, TP+SP is usually done only within a node (keeping the TP degree under the number of GPU per nodes, e.g. TP≤8).</p>
|
|
|
|
| 1214 |
|
| 1215 |
+
<p>We can benchmark how this communication overhead becomes increasingly problematic as we scale up tensor parallelism. Let’s measure the throughput and memory utilization as we scale TP with SP for a 3B model with 4096 seqlen:</p>
|
|
|
|
|
|
|
|
|
|
| 1216 |
|
| 1217 |
<iframe class="l-body-outset" id="plotFrame2" src="assets/data/benchmarks/tp_sp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1218 |
<script>
|
|
|
|
| 1224 |
</script>
|
| 1225 |
|
| 1226 |
<!-- <p><img alt="tp_sp_scaling.svg" src="/assets/images/tp_sp_scaling.svg" /></p> -->
|
| 1227 |
+
<p>Here again, there's a trade-off between computational efficiency (left) and memory capacity (right). While higher parallelism degrees enable processing of significantly larger batch sizes by reducing the activation memory, they also reduce per-GPU throughput, in particular above a threshold corresponding to the number of GPUs per node.</p>
|
| 1228 |
|
| 1229 |
<p>Let’s summarize our observations:</p>
|
| 1230 |
|
|
|
|
| 1239 |
<div class="note-box">
|
| 1240 |
<p class="note-box-title">📝 Note</p>
|
| 1241 |
<div class="note-box-content">
|
| 1242 |
+
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to all-reduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is however a small communication overhead since LayerNorm has relatively few parameters.</p>
|
| 1243 |
</div>
|
| 1244 |
</div>
|
| 1245 |
|
|
|
|
| 1249 |
|
| 1250 |
<h2>Context Parallelism</h2>
|
| 1251 |
|
| 1252 |
+
<p>With Tensor Parallelism and Sequence Parallelism, we can reduce the memory requirements per GPU significantly as both model weights and activations are distributed across GPUs. However, when training models on longer and longer sequences (e.g. when scaling to 128k or more tokens per sequence) we might still exceed the memory available on a single node as we still have to process a full sequence length when we're inside the TP region.</p>
|
| 1253 |
|
| 1254 |
+
<p>Moreover, even if we use full recomputation of the activations (which comes at a heavy compute overhead of ~30%), we still need to hold in memory some activations at the layer boundaries which scale linearly with sequence length. Let's take a look and see how Context Parallelism can help us:</p>
|
| 1255 |
|
| 1256 |
<iframe class="l-body-outset" id="plotFrame9" src="assets/data/benchmarks/cp_8Bmemoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1257 |
<script>
|
|
|
|
| 1264 |
|
| 1265 |
<!-- <p><img alt="image.png" src="/assets/images/cp_memoryusage.svg" /></p> -->
|
| 1266 |
|
| 1267 |
+
<p>The core idea of Context Parrallelism is to apply a similar idea to the Sequence Parallelism approach (aka to split along the sequence length) but to the modules where we already apply Tensor Parallelism. We will thus split these modules along two dimensions, thereby also reducing the effect of sequence length. You will find this approach quite intuitive after all we’ve already convered but... there is a trick to it so stay awake!</p>
|
| 1268 |
+
|
| 1269 |
+
<p>For Context Parallelism; just like Sequence Parallelism, we’ll split the input along the sequence dimension but we now apply this splitting along the full model, instead of only the sequence parallel regions of the model as we’ve done previous with Tensor + Sequence Parallelism.</p>
|
|
|
|
|
|
|
| 1270 |
|
| 1271 |
<!-- <p><img alt="cp_8Bmemoryusage.svg" src="/assets/images/cp_8Bmemoryusage.svg" /></p>
|
| 1272 |
-->
|
| 1273 |
<p>Splitting the sequence doesn't affect most modules like MLP and LayerNorm, where each token is processed independently. It also doesn’t require expensive communication like TP, as only the inputs are split and not the weight matrices. Just like data parallelism, after computing the gradients, an all-reduce operation is initiated to synchronize the gradients across the context parallelism group.</p>
|
| 1274 |
|
| 1275 |
+
<p>There is one important exception though as we we need to pay particular attention to the <strong>Attention blocks</strong> (haha.. pun intended :D). In the attention module each token needs to access key/value pairs from <strong>all</strong> other sequence tokens or in the case of causal attention at least attends to each previous token.</p>
|
| 1276 |
|
| 1277 |
+
<p>Because Context Parallelism splits the inputs along the sequence dimension across GPUs, the attention module will requires full communication between GPUs to exchange the necessary key/value data.</p>
|
| 1278 |
|
| 1279 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1280 |
|
|
|
|
| 1287 |
|
| 1288 |
<h3>Discovering Ring Attention</h3>
|
| 1289 |
|
| 1290 |
+
<p>In this implementation of the attention mechanism, each GPU first initiates an asynchronous communication operation to send its key/value pairs to other GPUs. While waiting for the other GPUs data, it computes the attention score for the portion of the data it already has in memory. Ideally, a next key/value pair is received from another GPU before this computation finishes, allowing the GPU to start the next round of computation immediately after it finishes its first computation.</p>
|
| 1291 |
|
| 1292 |
+
<p>Let's illustrate this. We'll suppose we have 4 GPUs and an input of 4 tokens. Initially, the input sequence is split evenly along the sequence dimension, so each GPU will have just one token along with its corresponding Q/K/V values. Leyt's say Q1, K1, and V1 represent the query, key, and value of the first token, which are located on the 1st GPU. The attention calculation will take 4 time steps to complete. At each time step, each GPU performs these three successive operations:</p>
|
| 1293 |
|
| 1294 |
<ol>
|
| 1295 |
+
<li>Send “current keys and values” to the next machine except during the last time step in a non-blocking manner so we can starts the following step before this step is finished</li>
|
| 1296 |
+
<li>Locally compute the attention score on the “current keys and values” it already has, which typically involves performing <d-math>Softmax(\frac{QK^T}{\sqrt{d}}) * V</d-math>d-math>.</li>
|
| 1297 |
+
<li>Wait to receive keys and values from the previous GPU and then circle back to step 1. where “current keys and values” are now the key/values just received from the previous GPU.</li>
|
| 1298 |
</ol>
|
| 1299 |
|
| 1300 |
+
<p>We perform these 3 steps four times to complete the attention calculation.</p>
|
| 1301 |
+
|
| 1302 |
<p>The whole process with 4 GPUs is shown in the following animation:</p>
|
| 1303 |
|
| 1304 |
<p><img alt="ring-attention.gif" src="/assets/images/ring-attention.gif" /></p>
|
| 1305 |
|
| 1306 |
+
<p>It's probably obvious to you on this animation why the authors chose to call this approach Ring Attention.</p>
|
| 1307 |
|
| 1308 |
+
<p>There is one big problem though which is that a naive implementation of Ring Attention lead to some strong imbalance between GPU coming from the shape of the causal attention matrix. Let’s take a look at the SoftMax computation by considering the attention score matrix with the causal attention mask:</p>
|
| 1309 |
|
| 1310 |
<p><img alt="cp_attnmask.svg" src="/assets/images/cp_attnmask.svg" /></p>
|
| 1311 |
|
|
|
|
| 1346 |
|
| 1347 |
<p>The All-to-All approach generally offers better memory efficiency at the cost of slightly more complex communication patterns, while the AllGather approach is simpler but requires more temporary memory during the attention computation.</p>
|
| 1348 |
|
| 1349 |
+
<p>We've now seen how we can split a model across one node with TP to tame large models and that we can use CP to tame the activation explosion with long sequences.</p>
|
| 1350 |
+
|
| 1351 |
+
<p>However, we still know that TP doesn't scale well across nodes, so what can we do if the model weights don't easily fit on 1 node? Here come another degree of parallelism, our forth one, called <strong>Pipeline Parallelism</strong>, to the rescue!</p>
|
| 1352 |
|
| 1353 |
<h2>Pipeline Parallelism</h2>
|
| 1354 |
|
src/index.html
CHANGED
|
@@ -983,25 +983,33 @@
|
|
| 983 |
|
| 984 |
<p>To come up with a strategy to follow, let’s move from a toy example to a real model building block. A Transformer model is made of two main building blocks : Feedforward layers (MLP) and Multi-Head Attention (MHA). We can apply tensor parallelism to both.</p>
|
| 985 |
|
| 986 |
-
<p>The Feedforward part can be parallelized by having a “Column linear” followed by a “Row Linear” which amounts to a broadcast to copy the input and an all-reduce in forward. Note that the broadcast isn’t needed in actual training where we can make sure inputs are already synced across TP ranks.</p>
|
| 987 |
|
| 988 |
<p><img alt="image.png" src="/assets/images/tp_diagram4.png" /></p>
|
| 989 |
|
| 990 |
-
<p>Now that we’ve found
|
| 991 |
|
| 992 |
<p>We can generally follow a similar approach where Q, K, and V matrices are split in a column-parallel fashion, and the output projection is split along the row dimension. With multi-head attention, the column-parallel approach has a very natural interpretation: each worker computes the attention for an individual or a subset of heads. The same approach works as well for <a href="https://arxiv.org/abs/1911.02150"><strong><em>multi-query</em></strong> (MQA)</a> or <a href="https://arxiv.org/abs/2305.13245"><strong><em>grouped query attention</em></strong> (GQA)</a> where key and values are shared between queries. </p>
|
| 993 |
|
| 994 |
-
<p>It's
|
| 995 |
|
| 996 |
<p><img alt="image.png" src="/assets/images/tp_full_diagram.png" /></p>
|
| 997 |
|
| 998 |
-
<p>Finally note that
|
| 999 |
|
| 1000 |
<p><img alt="Forward pass in Tensor Parallelism" src="/assets/images/tp_overlap.svg" /></p>
|
| 1001 |
|
|
|
|
|
|
|
| 1002 |
<p>Looking at the timeline of operations in tensor-parallel MLP (same applies for Attention), we can better understand the tradeoffs involved. In the forward of each decoder layer, we hit a synchronization point with the AllReduce operation that cannot be overlapped with computation. This <em>exposed communication</em> overhead is necessary to combine partial results across tensor-parallel ranks before the final LayerNorm can be applied. </p>
|
| 1003 |
|
| 1004 |
-
<
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1005 |
|
| 1006 |
<iframe class="l-body-outset" id="plotFrame13" src="assets/data/benchmarks/tp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1007 |
<script>
|
|
@@ -1014,11 +1022,11 @@
|
|
| 1014 |
<!--
|
| 1015 |
<p><img alt="Impact of Tensor Parallelism on model performance and batch size capacity: while increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training." src="/assets/images/tp_scaling.svg" /></p> -->
|
| 1016 |
|
| 1017 |
-
<p>
|
| 1018 |
|
| 1019 |
-
<p>In practice, the communication overhead of tensor parallelism becomes particularly noticeable as we scale beyond 8 GPUs. While tensor parallelism within a single node can leverage fast NVLink interconnects, going across nodes requires slower network connections.
|
| 1020 |
|
| 1021 |
-
<p>
|
| 1022 |
|
| 1023 |
<iframe class="l-body-outset" id="plotFrame7" src="assets/data/benchmarks/tp_memoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1024 |
<script>
|
|
@@ -1030,7 +1038,9 @@
|
|
| 1030 |
</script>
|
| 1031 |
<!-- <p><img alt="tp_memoryusage.svg" src="/assets/images/tp_memoryusage.svg" /></p> -->
|
| 1032 |
|
| 1033 |
-
<p>
|
|
|
|
|
|
|
| 1034 |
|
| 1035 |
<div class="note-box">
|
| 1036 |
<p class="note-box-title">📝 Note</p>
|
|
@@ -1039,24 +1049,22 @@
|
|
| 1039 |
</div>
|
| 1040 |
</div>
|
| 1041 |
|
| 1042 |
-
<p>
|
| 1043 |
|
| 1044 |
<h3>Sequence Parallelism</h3>
|
| 1045 |
|
| 1046 |
-
<p>
|
| 1047 |
-
|
| 1048 |
-
<p>Rather than gathering the full hidden dimension on each GPU (which would defeat the memory benefits of TP), we can instead shard these operations along the sequence length dimension. This approach is called <strong>sequence parallelism (SP)</strong>.</p>
|
| 1049 |
-
|
| 1050 |
<div class="note-box">
|
| 1051 |
-
|
| 1052 |
-
|
| 1053 |
-
|
| 1054 |
-
|
| 1055 |
-
|
| 1056 |
|
| 1057 |
-
|
| 1058 |
-
|
| 1059 |
-
|
| 1060 |
\text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta
|
| 1061 |
</d-math>
|
| 1062 |
|
|
@@ -1070,7 +1078,7 @@
|
|
| 1070 |
in backward: f = all-reduce ; f* = no-op ; g = reduce-scatter ; g* = all-gather
|
| 1071 |
SP region needs full hidden_dim" src="/assets/images/tp_sp_diagram.png" /></p>
|
| 1072 |
|
| 1073 |
-
<p>in forward: f = no-op ; f<em> = all-reduce ; g = all-gather ; g</em> = reduce-scatter in backward: f = all-reduce ; f<em> = no-op ; g = reduce-scatter ; g</em> = all-gather SP region needs full hidden_dim</p>
|
| 1074 |
|
| 1075 |
<p>The diagram shows how we transition between tensor-parallel and sequence-parallel regions using different collective operations (labeled "f" and "g"). The key challenge is managing these transitions efficiently while keeping memory usage low and maintaining correctness.</p>
|
| 1076 |
|
|
@@ -1194,19 +1202,17 @@
|
|
| 1194 |
</script>
|
| 1195 |
<!-- <p><img alt="tp_sp_memoryusage.svg" src="/assets/images/tp_sp_memoryusage.svg" /></p> -->
|
| 1196 |
|
| 1197 |
-
<p>
|
|
|
|
|
|
|
| 1198 |
|
| 1199 |
<p>If you’ve been paying close attention, you’ll notice that we’re talking about 4 comms ops in each layer (2 for Attention and 2 for MLP). This is how the MLP profiling looks like when using Tensor + Sequence Parallelism:</p>
|
| 1200 |
|
| 1201 |
<p><img alt="tp_sp_overlap.svg" src="/assets/images/tp_sp_overlap.svg" /></p>
|
| 1202 |
|
| 1203 |
-
<p>
|
| 1204 |
-
|
| 1205 |
|
| 1206 |
-
<
|
| 1207 |
-
|
| 1208 |
-
<p>As you might expect, this communication overhead becomes increasingly problematic as we scale up tensor parallelism. To illustrate this, let’s check throughput as we scale TP with SP for a 3B model:</p>
|
| 1209 |
-
<aside> For example, Megatron-LM/Nanotron implement a partial overlapping of all-gather with FC1 computation, and we expect to see more innovations in this space as the field continues to evolve.</aside>
|
| 1210 |
|
| 1211 |
<iframe class="l-body-outset" id="plotFrame2" src="assets/data/benchmarks/tp_sp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1212 |
<script>
|
|
@@ -1218,7 +1224,7 @@
|
|
| 1218 |
</script>
|
| 1219 |
|
| 1220 |
<!-- <p><img alt="tp_sp_scaling.svg" src="/assets/images/tp_sp_scaling.svg" /></p> -->
|
| 1221 |
-
<p>
|
| 1222 |
|
| 1223 |
<p>Let’s summarize our observations:</p>
|
| 1224 |
|
|
@@ -1233,7 +1239,7 @@
|
|
| 1233 |
<div class="note-box">
|
| 1234 |
<p class="note-box-title">📝 Note</p>
|
| 1235 |
<div class="note-box-content">
|
| 1236 |
-
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to all-reduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is a small communication overhead since LayerNorm has relatively few parameters.</p>
|
| 1237 |
</div>
|
| 1238 |
</div>
|
| 1239 |
|
|
@@ -1243,9 +1249,9 @@
|
|
| 1243 |
|
| 1244 |
<h2>Context Parallelism</h2>
|
| 1245 |
|
| 1246 |
-
<p>With Tensor Parallelism and Sequence Parallelism, we can reduce the memory requirements per GPU significantly as both model weights and activations are distributed across GPUs. However, when training models on longer and longer sequences (e.g. when scaling to 128k or more tokens per sequence) we might still exceed the memory available on a single node
|
| 1247 |
|
| 1248 |
-
<p>
|
| 1249 |
|
| 1250 |
<iframe class="l-body-outset" id="plotFrame9" src="assets/data/benchmarks/cp_8Bmemoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1251 |
<script>
|
|
@@ -1258,19 +1264,17 @@
|
|
| 1258 |
|
| 1259 |
<!-- <p><img alt="image.png" src="/assets/images/cp_memoryusage.svg" /></p> -->
|
| 1260 |
|
| 1261 |
-
<p>
|
| 1262 |
-
|
| 1263 |
-
<p>
|
| 1264 |
-
|
| 1265 |
-
<p>The idea of Context Parallelism is quite simple; just like Sequence Parallelism, we’ll split the input along the sequence dimension but we now apply this splitting along the full model, instead of only the sequence parallel regions of the model as we’ve done previous with Tensor + Sequence Parallelism.</p>
|
| 1266 |
|
| 1267 |
<!-- <p><img alt="cp_8Bmemoryusage.svg" src="/assets/images/cp_8Bmemoryusage.svg" /></p>
|
| 1268 |
-->
|
| 1269 |
<p>Splitting the sequence doesn't affect most modules like MLP and LayerNorm, where each token is processed independently. It also doesn’t require expensive communication like TP, as only the inputs are split and not the weight matrices. Just like data parallelism, after computing the gradients, an all-reduce operation is initiated to synchronize the gradients across the context parallelism group.</p>
|
| 1270 |
|
| 1271 |
-
<p>There is one important exception though
|
| 1272 |
|
| 1273 |
-
<p>Because Context Parallelism splits the inputs along the sequence dimension across GPUs, the attention module requires full communication between GPUs to exchange the necessary key/value data.</p>
|
| 1274 |
|
| 1275 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1276 |
|
|
@@ -1283,23 +1287,25 @@
|
|
| 1283 |
|
| 1284 |
<h3>Discovering Ring Attention</h3>
|
| 1285 |
|
| 1286 |
-
<p>In this implementation of attention, each GPU first initiates
|
| 1287 |
|
| 1288 |
-
<p>
|
| 1289 |
|
| 1290 |
<ol>
|
| 1291 |
-
<li>Send “current keys and values” to the next machine except during the last time step in a non-blocking manner so
|
| 1292 |
-
<li>
|
| 1293 |
-
<li>Wait to receive keys and values from the previous GPU and then
|
| 1294 |
</ol>
|
| 1295 |
|
|
|
|
|
|
|
| 1296 |
<p>The whole process with 4 GPUs is shown in the following animation:</p>
|
| 1297 |
|
| 1298 |
<p><img alt="ring-attention.gif" src="/assets/images/ring-attention.gif" /></p>
|
| 1299 |
|
| 1300 |
-
<p>
|
| 1301 |
|
| 1302 |
-
<p>There is one big problem though which is that a naive implementation of Ring Attention lead to some strong imbalance between GPU
|
| 1303 |
|
| 1304 |
<p><img alt="cp_attnmask.svg" src="/assets/images/cp_attnmask.svg" /></p>
|
| 1305 |
|
|
@@ -1340,7 +1346,9 @@
|
|
| 1340 |
|
| 1341 |
<p>The All-to-All approach generally offers better memory efficiency at the cost of slightly more complex communication patterns, while the AllGather approach is simpler but requires more temporary memory during the attention computation.</p>
|
| 1342 |
|
| 1343 |
-
<p>We've now seen how we can split a model across one node with TP to tame large models and that we can use CP to tame the activation explosion with long sequences
|
|
|
|
|
|
|
| 1344 |
|
| 1345 |
<h2>Pipeline Parallelism</h2>
|
| 1346 |
|
|
|
|
| 983 |
|
| 984 |
<p>To come up with a strategy to follow, let’s move from a toy example to a real model building block. A Transformer model is made of two main building blocks : Feedforward layers (MLP) and Multi-Head Attention (MHA). We can apply tensor parallelism to both.</p>
|
| 985 |
|
| 986 |
+
<p>The Feedforward part can be parallelized by having a “Column linear” followed by a “Row Linear” which amounts to a broadcast to copy the input and an all-reduce in forward. Note that the broadcast isn’t needed in actual training where we can make sure inputs are already synced across TP ranks. This setup is more efficient than starting with "Row Linear" followed by "Column Linear" as we can skip the intermediate all-reduce between both splitted operations.</p>
|
| 987 |
|
| 988 |
<p><img alt="image.png" src="/assets/images/tp_diagram4.png" /></p>
|
| 989 |
|
| 990 |
+
<p>Now that we’ve found an efficient schema for the Feedforward part of the transformer, let’s take a look at the multi-head attention block (MHA).</p>
|
| 991 |
|
| 992 |
<p>We can generally follow a similar approach where Q, K, and V matrices are split in a column-parallel fashion, and the output projection is split along the row dimension. With multi-head attention, the column-parallel approach has a very natural interpretation: each worker computes the attention for an individual or a subset of heads. The same approach works as well for <a href="https://arxiv.org/abs/1911.02150"><strong><em>multi-query</em></strong> (MQA)</a> or <a href="https://arxiv.org/abs/2305.13245"><strong><em>grouped query attention</em></strong> (GQA)</a> where key and values are shared between queries. </p>
|
| 993 |
|
| 994 |
+
<p>It's worth noting however that the tensor parallelism degree should not exceed the number of Q/K/V heads because we need intact heads per TP rank (otherwise we cannot compute the attentions independently on each GPU and we'll need additional communication operations). In case we’re using GQA, the TP degree should actually be smaller than the number of K/V heads. For instance, LLaMA-3 8B has 8 Key/Value heads, so the tensor parallelism degree should advantageously not exceed 8. If we use TP=16 for this model, we will need to duplicate the K/V heads on each GPU and make sure they stay in sync.</p>
|
| 995 |
|
| 996 |
<p><img alt="image.png" src="/assets/images/tp_full_diagram.png" /></p>
|
| 997 |
|
| 998 |
+
<p>Finally note that Tensor Parallelsim is still not a silver bullet for training. We’ve added several distributed communication primitive directly in the computation path of our model which are therefore hard to fully hide/overlap with computation (like we did in ZeRO), our final performances will be the results of a tradeoff between the computation and memory gains and the added communication overhead. Let's illustrate this:</p>
|
| 999 |
|
| 1000 |
<p><img alt="Forward pass in Tensor Parallelism" src="/assets/images/tp_overlap.svg" /></p>
|
| 1001 |
|
| 1002 |
+
<aside>It's possible to partially hide this communication by performing block matrix multiplication coupled with async communication/computation.</aside>
|
| 1003 |
+
|
| 1004 |
<p>Looking at the timeline of operations in tensor-parallel MLP (same applies for Attention), we can better understand the tradeoffs involved. In the forward of each decoder layer, we hit a synchronization point with the AllReduce operation that cannot be overlapped with computation. This <em>exposed communication</em> overhead is necessary to combine partial results across tensor-parallel ranks before the final LayerNorm can be applied. </p>
|
| 1005 |
|
| 1006 |
+
<aside>For example, Megatron-LM/Nanotron implement a partial overlapping of all-gather with FC1 computation where a portion of the matrix multiplication result will start to be sent to the other GPU while the other part is still being computed.</aside>
|
| 1007 |
+
|
| 1008 |
+
<p>Tensor parallelism does help reduce activation memory for the matrix multiplications since the intermediate activations are sharded across GPUs. However, we still need to gather the full activations for operations like LayerNorm, which means we're not getting the full memory benefits we could. Additionally, TP introduces significant communication requirements that heavily depend on the network infrastructure. The inability to fully hide this particular AllReduce behind computation means it directly adds to the critical path of forward propagation.</p>
|
| 1009 |
+
|
| 1010 |
+
<aside>This area of research is still an active area of research, with recent work like Domino <d-cite bibtex-key="wang2024domino"></d-cite> exploring novel techniques to maximize this overlap. </aside>
|
| 1011 |
+
|
| 1012 |
+
<p> Let's take a better look at the trade-off as we scale the TP degree:</p>
|
| 1013 |
|
| 1014 |
<iframe class="l-body-outset" id="plotFrame13" src="assets/data/benchmarks/tp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1015 |
<script>
|
|
|
|
| 1022 |
<!--
|
| 1023 |
<p><img alt="Impact of Tensor Parallelism on model performance and batch size capacity: while increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training." src="/assets/images/tp_scaling.svg" /></p> -->
|
| 1024 |
|
| 1025 |
+
<p>While increasing TP leads to reduced per-GPU throughput (left), it enables processing of larger batch sizes (right), illustrating the trade-off between computational efficiency and memory availability in distributed training.</p>
|
| 1026 |
|
| 1027 |
+
<p>In practice and as we see above on the left plot, the communication overhead of tensor parallelism becomes particularly noticeable as we scale beyond 8 GPUs. While tensor parallelism within a single node can leverage fast NVLink interconnects, going across nodes requires slower network connections. We observe significant drops when moving from TP=8 to TP=16, and an even steeper decline from TP=16 to TP=32. At higher degrees of parallelism, the communication overhead becomes so high that it quickly dominates the computation time.</p>
|
| 1028 |
|
| 1029 |
+
<p>This being said, tensor parallelism provides important benefits for memory usage by distributing model parameters, gradients, optimizer states and activations (to some extent) across GPUs. Let's examine this effect on a 70B parameter model:</p>
|
| 1030 |
|
| 1031 |
<iframe class="l-body-outset" id="plotFrame7" src="assets/data/benchmarks/tp_memoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1032 |
<script>
|
|
|
|
| 1038 |
</script>
|
| 1039 |
<!-- <p><img alt="tp_memoryusage.svg" src="/assets/images/tp_memoryusage.svg" /></p> -->
|
| 1040 |
|
| 1041 |
+
<p>Increasing tensor parallelism reduces the memory needed for model parameters, gradients and optimizer states on each GPU to the point where we can start fitting a large model on a single node of 8 GPUs. </p>
|
| 1042 |
+
|
| 1043 |
+
<p>Is there a way to get even more benefits from this technique? We've seen that layer normalization and dropout still require gathering the full activations on each GPU, partially negating the memory savings. We can do better by finding ways to parallelize these remaining operations as well.</p>
|
| 1044 |
|
| 1045 |
<div class="note-box">
|
| 1046 |
<p class="note-box-title">📝 Note</p>
|
|
|
|
| 1049 |
</div>
|
| 1050 |
</div>
|
| 1051 |
|
| 1052 |
+
<p>Let's explore next a small and natural extension to tensor parallelism, called <strong>Sequence Parallelism</strong> which does exactly that.</p>
|
| 1053 |
|
| 1054 |
<h3>Sequence Parallelism</h3>
|
| 1055 |
|
| 1056 |
+
<p><strong>Sequence parallelism (SP)</strong> involves splitting the activations and computations for the parts of the model not handled by tensor parallelism (TP) such as Dropout and LayerNorm, but along the input sequence dimension rather than across hidden dimension.</p>
|
| 1057 |
+
|
|
|
|
|
|
|
| 1058 |
<div class="note-box">
|
| 1059 |
+
<p class="note-box-title">📝 Note</p>
|
| 1060 |
+
<div class="note-box-content">
|
| 1061 |
+
<p>The term Sequence Parallelism is a bit overloaded: the Sequence Parallelism in this section is tightly coupled to Tensor Parallelism and applies to dropout and layer norm operation. However, when we will move to longer sequences the attention computation will become a bottleneck, which calls for techniques such as Ring-Attention, which are sometimes also called <em>Sequence Parallelism</em> but we’ll refer to them as <em>Context Parallelism</em> to differentiate the two approaches. So each time you see sequence parallelism, remember that it is used together with tensor parallelism (in contrast to context parallelism, which can be used independently).</p>
|
| 1062 |
+
</div>
|
| 1063 |
+
</div>
|
| 1064 |
|
| 1065 |
+
<p>This is needed because these operations require access to the full hidden dimension to compute correctly. For example, LayerNorm needs the full hidden dimension to compute mean and variance:</p>
|
| 1066 |
+
|
| 1067 |
+
<d-math block>
|
| 1068 |
\text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta
|
| 1069 |
</d-math>
|
| 1070 |
|
|
|
|
| 1078 |
in backward: f = all-reduce ; f* = no-op ; g = reduce-scatter ; g* = all-gather
|
| 1079 |
SP region needs full hidden_dim" src="/assets/images/tp_sp_diagram.png" /></p>
|
| 1080 |
|
| 1081 |
+
<p>Where the abbreviations are: in forward: f = no-op ; f<em> = all-reduce ; g = all-gather ; g</em> = reduce-scatter in backward: f = all-reduce ; f<em> = no-op ; g = reduce-scatter ; g</em> = all-gather SP region needs full hidden_dim</p>
|
| 1082 |
|
| 1083 |
<p>The diagram shows how we transition between tensor-parallel and sequence-parallel regions using different collective operations (labeled "f" and "g"). The key challenge is managing these transitions efficiently while keeping memory usage low and maintaining correctness.</p>
|
| 1084 |
|
|
|
|
| 1202 |
</script>
|
| 1203 |
<!-- <p><img alt="tp_sp_memoryusage.svg" src="/assets/images/tp_sp_memoryusage.svg" /></p> -->
|
| 1204 |
|
| 1205 |
+
<p>As we can see, we've again strongly reduced the maximum memory usage per GPU, allowing us to fit sequence lengths of 16k tokens with TP/SP=16, an improvement over the vanilla TP case! (TP=16 is still a bit large as we've seen in the previous section, but we'll see how we can improve this in the next section).</p>
|
| 1206 |
+
|
| 1207 |
+
<p>One question you may be asking yourself is whether using TP+SP incurs more communication than vanilla TP? Well, yes and no. In the forward pass of a vanilla TP we had two all-reduce per transformer block, and in SP we have two all-gather and two reduce-scatter per transformer block. So SP does twice the number of communication operations as TP. But since an all-reduce operation can be broken down into to an all-gather + reduce-scatter (see the <a target="_self" href="#a_quick_focus_on_ring_allreduce" class="">A quick focus on Ring AllReduce</a> section in the appendix) they’re actually equivalent in terms of communication. Same reasoning for backward as we just use the conjugate of each operation (no-op ↔ allreduce and allgather ↔ reducescatter).</p>
|
| 1208 |
|
| 1209 |
<p>If you’ve been paying close attention, you’ll notice that we’re talking about 4 comms ops in each layer (2 for Attention and 2 for MLP). This is how the MLP profiling looks like when using Tensor + Sequence Parallelism:</p>
|
| 1210 |
|
| 1211 |
<p><img alt="tp_sp_overlap.svg" src="/assets/images/tp_sp_overlap.svg" /></p>
|
| 1212 |
|
| 1213 |
+
<p>Just like vanilla TP, TP+SP can’t easily be overlapped with compute, which makes throughput heavily dependent on the communication bandwidth. Here again, like vanilla TO, TP+SP is usually done only within a node (keeping the TP degree under the number of GPU per nodes, e.g. TP≤8).</p>
|
|
|
|
| 1214 |
|
| 1215 |
+
<p>We can benchmark how this communication overhead becomes increasingly problematic as we scale up tensor parallelism. Let’s measure the throughput and memory utilization as we scale TP with SP for a 3B model with 4096 seqlen:</p>
|
|
|
|
|
|
|
|
|
|
| 1216 |
|
| 1217 |
<iframe class="l-body-outset" id="plotFrame2" src="assets/data/benchmarks/tp_sp_scaling.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1218 |
<script>
|
|
|
|
| 1224 |
</script>
|
| 1225 |
|
| 1226 |
<!-- <p><img alt="tp_sp_scaling.svg" src="/assets/images/tp_sp_scaling.svg" /></p> -->
|
| 1227 |
+
<p>Here again, there's a trade-off between computational efficiency (left) and memory capacity (right). While higher parallelism degrees enable processing of significantly larger batch sizes by reducing the activation memory, they also reduce per-GPU throughput, in particular above a threshold corresponding to the number of GPUs per node.</p>
|
| 1228 |
|
| 1229 |
<p>Let’s summarize our observations:</p>
|
| 1230 |
|
|
|
|
| 1239 |
<div class="note-box">
|
| 1240 |
<p class="note-box-title">📝 Note</p>
|
| 1241 |
<div class="note-box-content">
|
| 1242 |
+
<p>Since LayerNorms in the SP region operate on different portions of the sequence, their gradients will differ across TP ranks. To ensure the weights stay synchronized, we need to all-reduce their gradients during the backward pass, similar to how DP ensures weights stay in sync. This is however a small communication overhead since LayerNorm has relatively few parameters.</p>
|
| 1243 |
</div>
|
| 1244 |
</div>
|
| 1245 |
|
|
|
|
| 1249 |
|
| 1250 |
<h2>Context Parallelism</h2>
|
| 1251 |
|
| 1252 |
+
<p>With Tensor Parallelism and Sequence Parallelism, we can reduce the memory requirements per GPU significantly as both model weights and activations are distributed across GPUs. However, when training models on longer and longer sequences (e.g. when scaling to 128k or more tokens per sequence) we might still exceed the memory available on a single node as we still have to process a full sequence length when we're inside the TP region.</p>
|
| 1253 |
|
| 1254 |
+
<p>Moreover, even if we use full recomputation of the activations (which comes at a heavy compute overhead of ~30%), we still need to hold in memory some activations at the layer boundaries which scale linearly with sequence length. Let's take a look and see how Context Parallelism can help us:</p>
|
| 1255 |
|
| 1256 |
<iframe class="l-body-outset" id="plotFrame9" src="assets/data/benchmarks/cp_8Bmemoryusage.html" width="90%" scrolling="no" frameborder="0"></iframe>
|
| 1257 |
<script>
|
|
|
|
| 1264 |
|
| 1265 |
<!-- <p><img alt="image.png" src="/assets/images/cp_memoryusage.svg" /></p> -->
|
| 1266 |
|
| 1267 |
+
<p>The core idea of Context Parrallelism is to apply a similar idea to the Sequence Parallelism approach (aka to split along the sequence length) but to the modules where we already apply Tensor Parallelism. We will thus split these modules along two dimensions, thereby also reducing the effect of sequence length. You will find this approach quite intuitive after all we’ve already convered but... there is a trick to it so stay awake!</p>
|
| 1268 |
+
|
| 1269 |
+
<p>For Context Parallelism; just like Sequence Parallelism, we’ll split the input along the sequence dimension but we now apply this splitting along the full model, instead of only the sequence parallel regions of the model as we’ve done previous with Tensor + Sequence Parallelism.</p>
|
|
|
|
|
|
|
| 1270 |
|
| 1271 |
<!-- <p><img alt="cp_8Bmemoryusage.svg" src="/assets/images/cp_8Bmemoryusage.svg" /></p>
|
| 1272 |
-->
|
| 1273 |
<p>Splitting the sequence doesn't affect most modules like MLP and LayerNorm, where each token is processed independently. It also doesn’t require expensive communication like TP, as only the inputs are split and not the weight matrices. Just like data parallelism, after computing the gradients, an all-reduce operation is initiated to synchronize the gradients across the context parallelism group.</p>
|
| 1274 |
|
| 1275 |
+
<p>There is one important exception though as we we need to pay particular attention to the <strong>Attention blocks</strong> (haha.. pun intended :D). In the attention module each token needs to access key/value pairs from <strong>all</strong> other sequence tokens or in the case of causal attention at least attends to each previous token.</p>
|
| 1276 |
|
| 1277 |
+
<p>Because Context Parallelism splits the inputs along the sequence dimension across GPUs, the attention module will requires full communication between GPUs to exchange the necessary key/value data.</p>
|
| 1278 |
|
| 1279 |
<p>That sounds very expensive if we do it naively. Is there a way to do this rather efficiently and fast! Thankfully there is: a core technique to handle this communication of key/value pairs efficiently is called <em>Ring Attention</em>.</p>
|
| 1280 |
|
|
|
|
| 1287 |
|
| 1288 |
<h3>Discovering Ring Attention</h3>
|
| 1289 |
|
| 1290 |
+
<p>In this implementation of the attention mechanism, each GPU first initiates an asynchronous communication operation to send its key/value pairs to other GPUs. While waiting for the other GPUs data, it computes the attention score for the portion of the data it already has in memory. Ideally, a next key/value pair is received from another GPU before this computation finishes, allowing the GPU to start the next round of computation immediately after it finishes its first computation.</p>
|
| 1291 |
|
| 1292 |
+
<p>Let's illustrate this. We'll suppose we have 4 GPUs and an input of 4 tokens. Initially, the input sequence is split evenly along the sequence dimension, so each GPU will have just one token along with its corresponding Q/K/V values. Leyt's say Q1, K1, and V1 represent the query, key, and value of the first token, which are located on the 1st GPU. The attention calculation will take 4 time steps to complete. At each time step, each GPU performs these three successive operations:</p>
|
| 1293 |
|
| 1294 |
<ol>
|
| 1295 |
+
<li>Send “current keys and values” to the next machine except during the last time step in a non-blocking manner so we can starts the following step before this step is finished</li>
|
| 1296 |
+
<li>Locally compute the attention score on the “current keys and values” it already has, which typically involves performing <d-math>Softmax(\frac{QK^T}{\sqrt{d}}) * V</d-math>d-math>.</li>
|
| 1297 |
+
<li>Wait to receive keys and values from the previous GPU and then circle back to step 1. where “current keys and values” are now the key/values just received from the previous GPU.</li>
|
| 1298 |
</ol>
|
| 1299 |
|
| 1300 |
+
<p>We perform these 3 steps four times to complete the attention calculation.</p>
|
| 1301 |
+
|
| 1302 |
<p>The whole process with 4 GPUs is shown in the following animation:</p>
|
| 1303 |
|
| 1304 |
<p><img alt="ring-attention.gif" src="/assets/images/ring-attention.gif" /></p>
|
| 1305 |
|
| 1306 |
+
<p>It's probably obvious to you on this animation why the authors chose to call this approach Ring Attention.</p>
|
| 1307 |
|
| 1308 |
+
<p>There is one big problem though which is that a naive implementation of Ring Attention lead to some strong imbalance between GPU coming from the shape of the causal attention matrix. Let’s take a look at the SoftMax computation by considering the attention score matrix with the causal attention mask:</p>
|
| 1309 |
|
| 1310 |
<p><img alt="cp_attnmask.svg" src="/assets/images/cp_attnmask.svg" /></p>
|
| 1311 |
|
|
|
|
| 1346 |
|
| 1347 |
<p>The All-to-All approach generally offers better memory efficiency at the cost of slightly more complex communication patterns, while the AllGather approach is simpler but requires more temporary memory during the attention computation.</p>
|
| 1348 |
|
| 1349 |
+
<p>We've now seen how we can split a model across one node with TP to tame large models and that we can use CP to tame the activation explosion with long sequences.</p>
|
| 1350 |
+
|
| 1351 |
+
<p>However, we still know that TP doesn't scale well across nodes, so what can we do if the model weights don't easily fit on 1 node? Here come another degree of parallelism, our forth one, called <strong>Pipeline Parallelism</strong>, to the rescue!</p>
|
| 1352 |
|
| 1353 |
<h2>Pipeline Parallelism</h2>
|
| 1354 |
|