another pass (#64)
Browse files- fixes (3f0047661e2970a8c23bfde354ba36508eb1c6ad)
- dist/assets/images/memorycoalescing.png +2 -2
- dist/bibliography.bib +1 -1
- dist/fragments/benchmarks_interactive.html +0 -0
- dist/index.html +6 -5
- src/bibliography.bib +1 -1
- src/fragments/benchmarks_interactive.html +0 -0
- src/index.html +7 -6
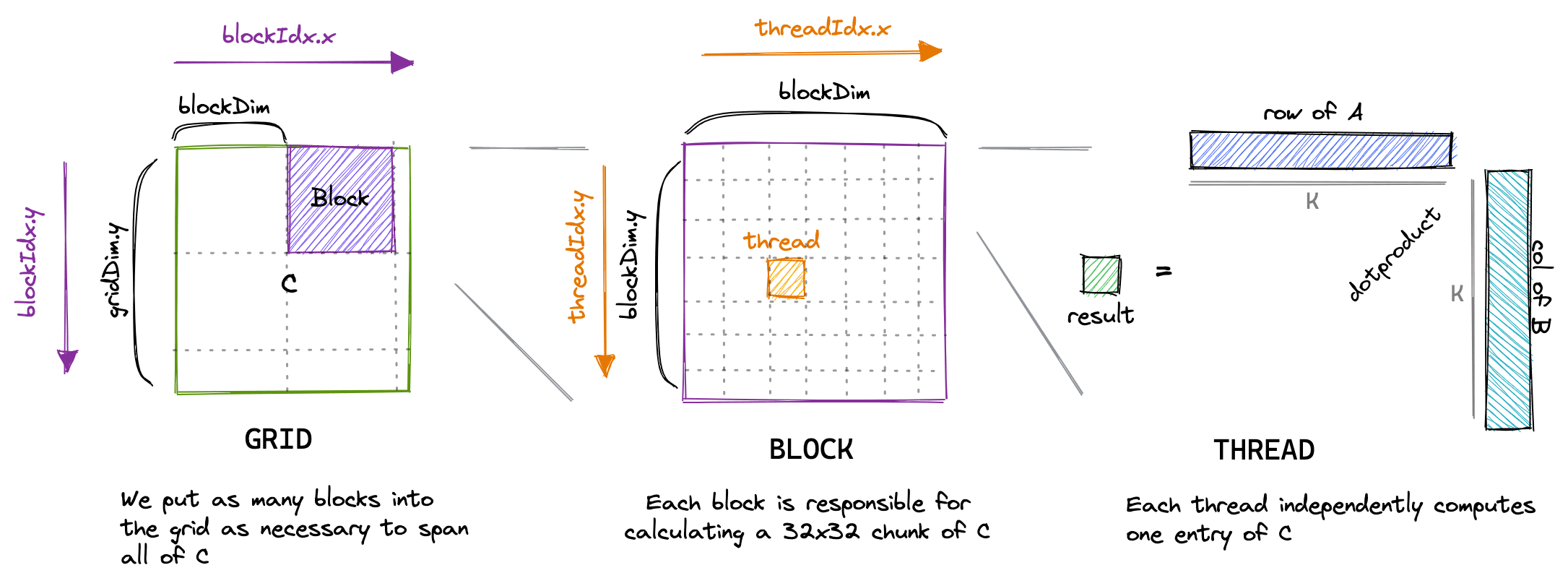
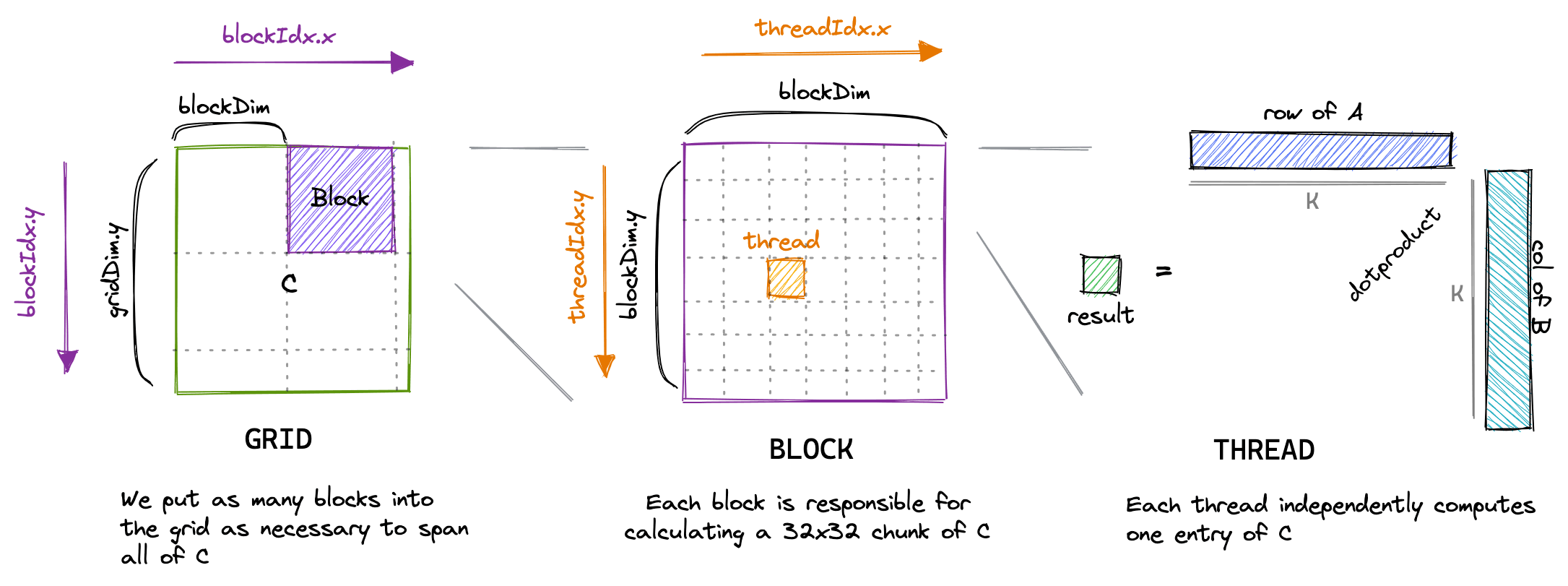
dist/assets/images/memorycoalescing.png
CHANGED
|
Git LFS Details
|
|
Git LFS Details
|
dist/bibliography.bib
CHANGED
|
@@ -361,7 +361,7 @@ url = {https://github.com/meta-llama/llama3/blob/main/MODEL_CARD.md}
|
|
| 361 |
}
|
| 362 |
@misc{deepseekai2024deepseekv3technicalreport,
|
| 363 |
title={DeepSeek-V3 Technical Report},
|
| 364 |
-
author={DeepSeek-AI and
|
| 365 |
year={2024},
|
| 366 |
eprint={2412.19437},
|
| 367 |
archivePrefix={arXiv},
|
|
|
|
| 361 |
}
|
| 362 |
@misc{deepseekai2024deepseekv3technicalreport,
|
| 363 |
title={DeepSeek-V3 Technical Report},
|
| 364 |
+
author={DeepSeek-AI and others},
|
| 365 |
year={2024},
|
| 366 |
eprint={2412.19437},
|
| 367 |
archivePrefix={arXiv},
|
dist/fragments/benchmarks_interactive.html
CHANGED
|
The diff for this file is too large to render.
See raw diff
|
|
|
dist/index.html
CHANGED
|
@@ -861,7 +861,7 @@
|
|
| 861 |
|
| 862 |
<p>In ZeRO-1, the optimizer states are partitioned into <d-math>N_d</d-math> equal parts where <d-math>N_d</d-math> is the DP degree. This means that each model replica distributed on each DP rank only keeps track of <d-math>\frac{1}{N_d}</d-math> of the optimizer states. During the optimization step only <d-math>\frac{1}{N_d}</d-math> of the float32 weights are updated.</p>
|
| 863 |
|
| 864 |
-
<p>However during the forward pass, each replica
|
| 865 |
|
| 866 |
<p>This explains the memory formula of <d-math>2\Psi + 2\Psi + \frac{k\Psi}{N_d}</d-math> that we saw on the above graph! Here’s a summary of the sequence of operations for a single training step</p>
|
| 867 |
|
|
@@ -1000,7 +1000,7 @@
|
|
| 1000 |
|
| 1001 |
<p>In practice a small example of the operation looks like this:</p>
|
| 1002 |
|
| 1003 |
-
<p
|
| 1004 |
|
| 1005 |
<p>Let’s see how we can parallelise this operation! In tensor parallelism, tensors will be split into N shards along a particular dimension and distributed across N GPUs. Matrices can be split either on the column part or row part leading to row and column parallelism. One thing we’ll see in the following is that choosing row or column sharding will require different communications primitives.</p>
|
| 1006 |
|
|
@@ -1377,7 +1377,7 @@
|
|
| 1377 |
|
| 1378 |
<h3>Zig-Zag Ring Attention – A Balanced Compute Implementation</h3>
|
| 1379 |
|
| 1380 |
-
<p>We need a better way to distribute the input sequences. This can be achieved by assigning the tokens not purely sequential to the GPUs but by mixing the ordering a bit such that we have a good mix of early and late tokens on each GPU. This approach is called Zig-Zag attention<d-cite bibtex-key="
|
| 1381 |
|
| 1382 |
<p><img alt="cp_zigzagmask.svg" src="/assets/images/cp_zigzagmask.svg" /></p>
|
| 1383 |
|
|
@@ -2862,8 +2862,9 @@
|
|
| 2862 |
</div>
|
| 2863 |
|
| 2864 |
<div>
|
| 2865 |
-
<a href="https://main-horse.github.io/posts/visualizing-6d/"><strong
|
| 2866 |
-
|
|
|
|
| 2867 |
</div>
|
| 2868 |
|
| 2869 |
<h3>Hardware</h3>
|
|
|
|
| 861 |
|
| 862 |
<p>In ZeRO-1, the optimizer states are partitioned into <d-math>N_d</d-math> equal parts where <d-math>N_d</d-math> is the DP degree. This means that each model replica distributed on each DP rank only keeps track of <d-math>\frac{1}{N_d}</d-math> of the optimizer states. During the optimization step only <d-math>\frac{1}{N_d}</d-math> of the float32 weights are updated.</p>
|
| 863 |
|
| 864 |
+
<p>However during the forward pass, each replica need all the parameters, we thus need to add an additional <strong><em>all-gather</em></strong> (the second type of collective communication primitive we encounter!) after the optimizer step so that each model replica has the full set of updated weights.</p>
|
| 865 |
|
| 866 |
<p>This explains the memory formula of <d-math>2\Psi + 2\Psi + \frac{k\Psi}{N_d}</d-math> that we saw on the above graph! Here’s a summary of the sequence of operations for a single training step</p>
|
| 867 |
|
|
|
|
| 1000 |
|
| 1001 |
<p>In practice a small example of the operation looks like this:</p>
|
| 1002 |
|
| 1003 |
+
<p style="text-align: center"><img width="300px" alt="TP diagram" src="/assets/images/tp_diagram.svg" /></p>
|
| 1004 |
|
| 1005 |
<p>Let’s see how we can parallelise this operation! In tensor parallelism, tensors will be split into N shards along a particular dimension and distributed across N GPUs. Matrices can be split either on the column part or row part leading to row and column parallelism. One thing we’ll see in the following is that choosing row or column sharding will require different communications primitives.</p>
|
| 1006 |
|
|
|
|
| 1377 |
|
| 1378 |
<h3>Zig-Zag Ring Attention – A Balanced Compute Implementation</h3>
|
| 1379 |
|
| 1380 |
+
<p>We need a better way to distribute the input sequences. This can be achieved by assigning the tokens not purely sequential to the GPUs but by mixing the ordering a bit such that we have a good mix of early and late tokens on each GPU. This approach is called Zig-Zag attention<d-cite bibtex-key="brandon2023fasterring"></d-cite> and in this new arrangement, the attention mask will show an even distribution of computation but if you count the number of colored squares, you’ll see that the computation is now balanced across all GPUs.</p>
|
| 1381 |
|
| 1382 |
<p><img alt="cp_zigzagmask.svg" src="/assets/images/cp_zigzagmask.svg" /></p>
|
| 1383 |
|
|
|
|
| 2862 |
</div>
|
| 2863 |
|
| 2864 |
<div>
|
| 2865 |
+
<a href="https://main-horse.github.io/posts/visualizing-6d/"><strong>Visualizing 6D Mesh Parallelism
|
| 2866 |
+
</strong></a>
|
| 2867 |
+
<p>Explains the collective communication involved in a 6D parallel mesh.</p>
|
| 2868 |
</div>
|
| 2869 |
|
| 2870 |
<h3>Hardware</h3>
|
src/bibliography.bib
CHANGED
|
@@ -361,7 +361,7 @@ url = {https://github.com/meta-llama/llama3/blob/main/MODEL_CARD.md}
|
|
| 361 |
}
|
| 362 |
@misc{deepseekai2024deepseekv3technicalreport,
|
| 363 |
title={DeepSeek-V3 Technical Report},
|
| 364 |
-
author={DeepSeek-AI and
|
| 365 |
year={2024},
|
| 366 |
eprint={2412.19437},
|
| 367 |
archivePrefix={arXiv},
|
|
|
|
| 361 |
}
|
| 362 |
@misc{deepseekai2024deepseekv3technicalreport,
|
| 363 |
title={DeepSeek-V3 Technical Report},
|
| 364 |
+
author={DeepSeek-AI and others},
|
| 365 |
year={2024},
|
| 366 |
eprint={2412.19437},
|
| 367 |
archivePrefix={arXiv},
|
src/fragments/benchmarks_interactive.html
CHANGED
|
The diff for this file is too large to render.
See raw diff
|
|
|
src/index.html
CHANGED
|
@@ -861,7 +861,7 @@
|
|
| 861 |
|
| 862 |
<p>In ZeRO-1, the optimizer states are partitioned into <d-math>N_d</d-math> equal parts where <d-math>N_d</d-math> is the DP degree. This means that each model replica distributed on each DP rank only keeps track of <d-math>\frac{1}{N_d}</d-math> of the optimizer states. During the optimization step only <d-math>\frac{1}{N_d}</d-math> of the float32 weights are updated.</p>
|
| 863 |
|
| 864 |
-
<p>However during the forward pass, each replica
|
| 865 |
|
| 866 |
<p>This explains the memory formula of <d-math>2\Psi + 2\Psi + \frac{k\Psi}{N_d}</d-math> that we saw on the above graph! Here’s a summary of the sequence of operations for a single training step</p>
|
| 867 |
|
|
@@ -1000,7 +1000,7 @@
|
|
| 1000 |
|
| 1001 |
<p>In practice a small example of the operation looks like this:</p>
|
| 1002 |
|
| 1003 |
-
<p
|
| 1004 |
|
| 1005 |
<p>Let’s see how we can parallelise this operation! In tensor parallelism, tensors will be split into N shards along a particular dimension and distributed across N GPUs. Matrices can be split either on the column part or row part leading to row and column parallelism. One thing we’ll see in the following is that choosing row or column sharding will require different communications primitives.</p>
|
| 1006 |
|
|
@@ -1377,7 +1377,7 @@
|
|
| 1377 |
|
| 1378 |
<h3>Zig-Zag Ring Attention – A Balanced Compute Implementation</h3>
|
| 1379 |
|
| 1380 |
-
<p>We need a better way to distribute the input sequences. This can be achieved by assigning the tokens not purely sequential to the GPUs but by mixing the ordering a bit such that we have a good mix of early and late tokens on each GPU. This approach is called Zig-Zag attention<d-cite bibtex-key="
|
| 1381 |
|
| 1382 |
<p><img alt="cp_zigzagmask.svg" src="/assets/images/cp_zigzagmask.svg" /></p>
|
| 1383 |
|
|
@@ -1874,7 +1874,7 @@
|
|
| 1874 |
|
| 1875 |
<p>Clearly, none of these techniques is a silver bullet for magical scaling and we'll often have to combine them in one way or another. Can we actually come up with a few rules that would help us find a good starting point to choose among –and combine– them? This will be the topic of our next section.</p>
|
| 1876 |
|
| 1877 |
-
<h2>
|
| 1878 |
|
| 1879 |
<p>We’ve now covered all the parallelism techniques that are actually used to distribute and training larger models as well as how and why they can be combined together. There remain a general question: which ones should we choose in the end and how to decide on a specific combination?</p>
|
| 1880 |
|
|
@@ -2862,8 +2862,9 @@
|
|
| 2862 |
</div>
|
| 2863 |
|
| 2864 |
<div>
|
| 2865 |
-
<a href="https://main-horse.github.io/posts/visualizing-6d/"><strong
|
| 2866 |
-
|
|
|
|
| 2867 |
</div>
|
| 2868 |
|
| 2869 |
<h3>Hardware</h3>
|
|
|
|
| 861 |
|
| 862 |
<p>In ZeRO-1, the optimizer states are partitioned into <d-math>N_d</d-math> equal parts where <d-math>N_d</d-math> is the DP degree. This means that each model replica distributed on each DP rank only keeps track of <d-math>\frac{1}{N_d}</d-math> of the optimizer states. During the optimization step only <d-math>\frac{1}{N_d}</d-math> of the float32 weights are updated.</p>
|
| 863 |
|
| 864 |
+
<p>However during the forward pass, each replica need all the parameters, we thus need to add an additional <strong><em>all-gather</em></strong> (the second type of collective communication primitive we encounter!) after the optimizer step so that each model replica has the full set of updated weights.</p>
|
| 865 |
|
| 866 |
<p>This explains the memory formula of <d-math>2\Psi + 2\Psi + \frac{k\Psi}{N_d}</d-math> that we saw on the above graph! Here’s a summary of the sequence of operations for a single training step</p>
|
| 867 |
|
|
|
|
| 1000 |
|
| 1001 |
<p>In practice a small example of the operation looks like this:</p>
|
| 1002 |
|
| 1003 |
+
<p style="text-align: center"><img width="300px" alt="TP diagram" src="/assets/images/tp_diagram.svg" /></p>
|
| 1004 |
|
| 1005 |
<p>Let’s see how we can parallelise this operation! In tensor parallelism, tensors will be split into N shards along a particular dimension and distributed across N GPUs. Matrices can be split either on the column part or row part leading to row and column parallelism. One thing we’ll see in the following is that choosing row or column sharding will require different communications primitives.</p>
|
| 1006 |
|
|
|
|
| 1377 |
|
| 1378 |
<h3>Zig-Zag Ring Attention – A Balanced Compute Implementation</h3>
|
| 1379 |
|
| 1380 |
+
<p>We need a better way to distribute the input sequences. This can be achieved by assigning the tokens not purely sequential to the GPUs but by mixing the ordering a bit such that we have a good mix of early and late tokens on each GPU. This approach is called Zig-Zag attention<d-cite bibtex-key="brandon2023fasterring"></d-cite> and in this new arrangement, the attention mask will show an even distribution of computation but if you count the number of colored squares, you’ll see that the computation is now balanced across all GPUs.</p>
|
| 1381 |
|
| 1382 |
<p><img alt="cp_zigzagmask.svg" src="/assets/images/cp_zigzagmask.svg" /></p>
|
| 1383 |
|
|
|
|
| 1874 |
|
| 1875 |
<p>Clearly, none of these techniques is a silver bullet for magical scaling and we'll often have to combine them in one way or another. Can we actually come up with a few rules that would help us find a good starting point to choose among –and combine– them? This will be the topic of our next section.</p>
|
| 1876 |
|
| 1877 |
+
<h2>Finding the Best Training Configuration</h2>
|
| 1878 |
|
| 1879 |
<p>We’ve now covered all the parallelism techniques that are actually used to distribute and training larger models as well as how and why they can be combined together. There remain a general question: which ones should we choose in the end and how to decide on a specific combination?</p>
|
| 1880 |
|
|
|
|
| 2862 |
</div>
|
| 2863 |
|
| 2864 |
<div>
|
| 2865 |
+
<a href="https://main-horse.github.io/posts/visualizing-6d/"><strong>Visualizing 6D Mesh Parallelism
|
| 2866 |
+
</strong></a>
|
| 2867 |
+
<p>Explains the collective communication involved in a 6D parallel mesh.</p>
|
| 2868 |
</div>
|
| 2869 |
|
| 2870 |
<h3>Hardware</h3>
|