problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Find all pairs of positive integers $(a, b)$ satisfying the following conditions: (i) $a$ divides $b^{4}+1$, (ii) $b$ divides $a^{4}+1$, (iii) $\lfloor\sqrt{a}\rfloor=\lfloor\sqrt{b}\rfloor$.
|
Obviously, $\operatorname{gcd}(a, b)=1$, so the problem conditions imply $$ a b \mid(a-b)^{4}+1 $$ since each of $a$ and $b$ divide the right-hand side. We define $$ k \stackrel{\text { def }}{=} \frac{(b-a)^{4}+1}{a b} . $$ Claim (Size estimate) — We must have $k \leq 16$. $$ \begin{aligned} a b & \geq n^{2}\left(n^{2}+1\right) \geq n^{4}+1 \\ (b-a)^{4}+1 & \leq(2 n)^{4}+1=16 n^{4}+1 \end{aligned} $$ which shows $k \leq 16$. Claim (Orders argument) - In fact, $k=1$. Thus $k$ is odd. However, every odd prime divisor of $(b-a)^{4}+1$ is congruent to 1 $(\bmod 8)$ and is thus at least 17 , so $k=1$ or $k \geq 17$. It follows that $k=1$. At this point, we have reduced to solving $$ a b=(b-a)^{4}+1 $$ $$ a^{2}-d a-\left(d^{4}+1\right)=0 $$ The discriminant $d^{2}+4\left(d^{4}+1\right)=4 d^{4}+d^{2}+4$ must be a perfect square. - The cases $d=0$ and $d=1$ lead to pairs $(1,1)$ and $(1,2)$. - If $d \geq 2$, then we can sandwich $$ \left(2 d^{2}\right)^{2}<4 d^{4}+d^{2}+4<4 d^{4}+4 d^{2}+1=\left(2 d^{2}+1\right)^{2} $$ so the discriminant is not a square. Remark (Author remarks on origin). This comes from the problem of the existence of a pair of elliptic curves over $\mathbb{F}_{a}, \mathbb{F}_{b}$ respectively, such that the number of points on one is the field size of the other. The bound $n^{2} \leq a, b<(n+1)^{2}$ is the Hasse bound. The divisibility conditions correspond to asserting that the embedding degree of each curve is 8 , so that they are pairing friendly. In this way, the problem is essentially the key result of https://arxiv.org/pdf/1803.02067.pdf, shown in Proposition 3.
|
(1,1), (1,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of positive integers $(a, b)$ satisfying the following conditions: (i) $a$ divides $b^{4}+1$, (ii) $b$ divides $a^{4}+1$, (iii) $\lfloor\sqrt{a}\rfloor=\lfloor\sqrt{b}\rfloor$.
|
Obviously, $\operatorname{gcd}(a, b)=1$, so the problem conditions imply $$ a b \mid(a-b)^{4}+1 $$ since each of $a$ and $b$ divide the right-hand side. We define $$ k \stackrel{\text { def }}{=} \frac{(b-a)^{4}+1}{a b} . $$ Claim (Size estimate) — We must have $k \leq 16$. $$ \begin{aligned} a b & \geq n^{2}\left(n^{2}+1\right) \geq n^{4}+1 \\ (b-a)^{4}+1 & \leq(2 n)^{4}+1=16 n^{4}+1 \end{aligned} $$ which shows $k \leq 16$. Claim (Orders argument) - In fact, $k=1$. Thus $k$ is odd. However, every odd prime divisor of $(b-a)^{4}+1$ is congruent to 1 $(\bmod 8)$ and is thus at least 17 , so $k=1$ or $k \geq 17$. It follows that $k=1$. At this point, we have reduced to solving $$ a b=(b-a)^{4}+1 $$ $$ a^{2}-d a-\left(d^{4}+1\right)=0 $$ The discriminant $d^{2}+4\left(d^{4}+1\right)=4 d^{4}+d^{2}+4$ must be a perfect square. - The cases $d=0$ and $d=1$ lead to pairs $(1,1)$ and $(1,2)$. - If $d \geq 2$, then we can sandwich $$ \left(2 d^{2}\right)^{2}<4 d^{4}+d^{2}+4<4 d^{4}+4 d^{2}+1=\left(2 d^{2}+1\right)^{2} $$ so the discriminant is not a square. Remark (Author remarks on origin). This comes from the problem of the existence of a pair of elliptic curves over $\mathbb{F}_{a}, \mathbb{F}_{b}$ respectively, such that the number of points on one is the field size of the other. The bound $n^{2} \leq a, b<(n+1)^{2}$ is the Hasse bound. The divisibility conditions correspond to asserting that the embedding degree of each curve is 8 , so that they are pairing friendly. In this way, the problem is essentially the key result of https://arxiv.org/pdf/1803.02067.pdf, shown in Proposition 3.
|
{
"exam": "USA_TSTST",
"problem_label": "4",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
Suppose $|S| \geq 2$. For any $p \in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \notin S$ and $|R(p)|$ is even. 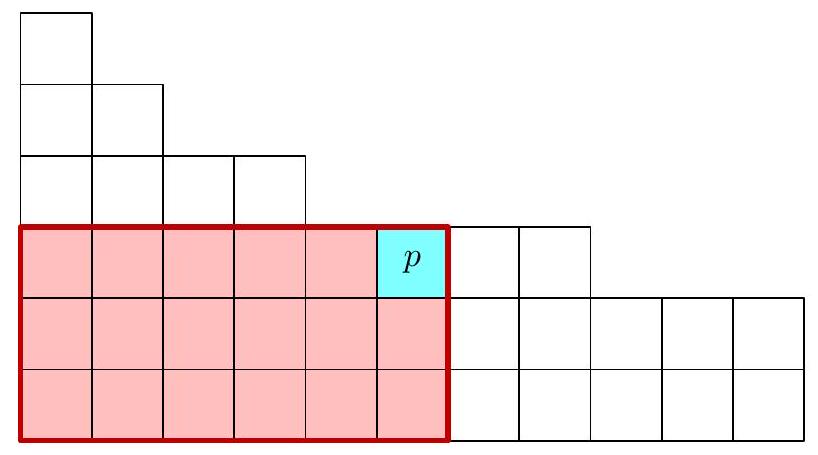 Claim - If $|S| \geq 2$, then a pivotal $p$ always exists. - If it has length at least 2 , one of the two rightmost points in it is pivotal. - Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \geq 2$ ) is pivotal. We describe how to complete the induction, given some pivotal $p \in S$. There is a partition $$ S=R(p) \sqcup S_{1} \sqcup S_{2} $$ where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty). Claim - The desired inequality holds for stable subsets containing $p$. Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \geq O_{1}$ and $E_{2} \geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \geq E_{1} O_{2}+E_{2} O_{1}$ as desired. By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
Suppose $|S| \geq 2$. For any $p \in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \notin S$ and $|R(p)|$ is even.  Claim - If $|S| \geq 2$, then a pivotal $p$ always exists. - If it has length at least 2 , one of the two rightmost points in it is pivotal. - Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \geq 2$ ) is pivotal. We describe how to complete the induction, given some pivotal $p \in S$. There is a partition $$ S=R(p) \sqcup S_{1} \sqcup S_{2} $$ where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty). Claim - The desired inequality holds for stable subsets containing $p$. Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \geq O_{1}$ and $E_{2} \geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \geq E_{1} O_{2}+E_{2} O_{1}$ as desired. By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\triangle A B C$. 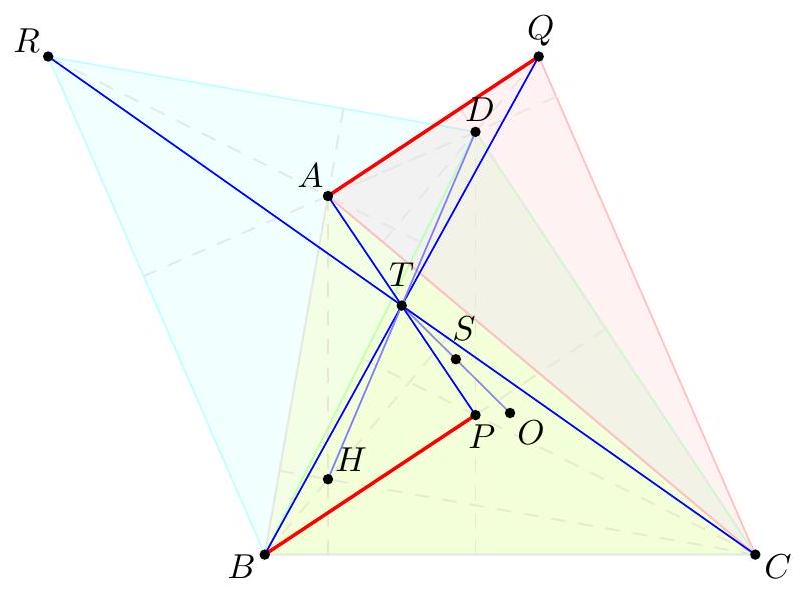 Claim (Key claim) - $T$ is the midpoint of $\overline{A P}, \overline{B Q}, \overline{C R}, \overline{D H}$, and $D$ is the orthocenter of $\triangle P Q R$. By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\overline{A P}, \overline{B Q}, \overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed $$ \frac{A T}{T P}=\frac{T Q}{B T}=\frac{C T}{T R}=\frac{T P}{A T} $$ so all the ratios are equal to +1 . Next, $\overline{P D} \perp \overline{B C} \| \overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\triangle P Q R$. This means that $T$ is the midpoint of $\overline{D H}$ as well. ## Corollary The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$. Let $S$ be the centroid of $\{A, B, C, D\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude: Claim - $A, B, C, D$ are equidistant from $O$. Then $T^{\prime}$ is the midpoint of $\overline{A^{\prime} D^{\prime}}$, so $S^{\prime}=\frac{1}{4}\left(A^{\prime}+D^{\prime}+B+C\right)$ gives that $O^{\prime}$ is the midpoint of $\overline{B C}$. Thus $O B=O C$ and we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\triangle A B C$.  Claim (Key claim) - $T$ is the midpoint of $\overline{A P}, \overline{B Q}, \overline{C R}, \overline{D H}$, and $D$ is the orthocenter of $\triangle P Q R$. By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\overline{A P}, \overline{B Q}, \overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed $$ \frac{A T}{T P}=\frac{T Q}{B T}=\frac{C T}{T R}=\frac{T P}{A T} $$ so all the ratios are equal to +1 . Next, $\overline{P D} \perp \overline{B C} \| \overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\triangle P Q R$. This means that $T$ is the midpoint of $\overline{D H}$ as well. ## Corollary The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$. Let $S$ be the centroid of $\{A, B, C, D\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude: Claim - $A, B, C, D$ are equidistant from $O$. Then $T^{\prime}$ is the midpoint of $\overline{A^{\prime} D^{\prime}}$, so $S^{\prime}=\frac{1}{4}\left(A^{\prime}+D^{\prime}+B+C\right)$ gives that $O^{\prime}$ is the midpoint of $\overline{B C}$. Thus $O B=O C$ and we're done.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.
|
The answer is $P(x)$ should be a polynomial of the form $P(x)=\lambda x^{n}-\mu$ where $|\lambda|=|\mu|$ and $\operatorname{Re} \mu=-\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. \l First approach (Evan Chen). We introduce the following notations: $$ \begin{aligned} P(x) & =c_{n} x^{n}+c_{n-1} x^{n-1}+\cdots+c_{1} x+c_{0} \\ & =c_{n}\left(x+\alpha_{1}\right) \ldots\left(x+\alpha_{n}\right) \\ P(x)-1 & =c_{n}\left(x+\beta_{1}\right) \ldots\left(x+\beta_{n}\right) \end{aligned} $$ By taking conjugates, $$ \begin{aligned} \left(x+\alpha_{1}\right) \cdots\left(x+\alpha_{n}\right) & =\left(x+\beta_{1}\right) \cdots\left(x+\beta_{n}\right)+c_{n}^{-1} \\ \Longrightarrow\left(x+\frac{1}{\alpha_{1}}\right) \cdots\left(x+\frac{1}{\alpha_{n}}\right) & =\left(x+\frac{1}{\beta_{1}}\right) \cdots\left(x+\frac{1}{\beta_{n}}\right)+\left(\overline{c_{n}}\right)^{-1} \end{aligned} $$ The equation $(\boldsymbol{\oplus})$ is the main player: Claim - We have $c_{k}=0$ for all $k=1, \ldots, n-1$. $$ \frac{c_{n-k}}{\prod_{i} \alpha_{i}}=\frac{c_{n-k}}{\prod_{i} \beta_{i}} $$ but $\prod_{i} \alpha_{i}-\prod_{i} \beta_{i}=\frac{1}{c_{n}} \neq 0$. Hence $c_{k}=0$. It follows that $P(x)$ must be of the form $P(x)=\lambda x^{n}-\mu$, so that $P(x)=\lambda x^{n}-(\mu+1)$. This requires $|\mu|=|\mu+1|=|\lambda|$ which is equivalent to the stated part.
|
P(x)=\lambda x^{n}-\mu \text{ where } |\lambda|=|\mu| \text{ and } \operatorname{Re} \mu=-\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.
|
The answer is $P(x)$ should be a polynomial of the form $P(x)=\lambda x^{n}-\mu$ where $|\lambda|=|\mu|$ and $\operatorname{Re} \mu=-\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. \l First approach (Evan Chen). We introduce the following notations: $$ \begin{aligned} P(x) & =c_{n} x^{n}+c_{n-1} x^{n-1}+\cdots+c_{1} x+c_{0} \\ & =c_{n}\left(x+\alpha_{1}\right) \ldots\left(x+\alpha_{n}\right) \\ P(x)-1 & =c_{n}\left(x+\beta_{1}\right) \ldots\left(x+\beta_{n}\right) \end{aligned} $$ By taking conjugates, $$ \begin{aligned} \left(x+\alpha_{1}\right) \cdots\left(x+\alpha_{n}\right) & =\left(x+\beta_{1}\right) \cdots\left(x+\beta_{n}\right)+c_{n}^{-1} \\ \Longrightarrow\left(x+\frac{1}{\alpha_{1}}\right) \cdots\left(x+\frac{1}{\alpha_{n}}\right) & =\left(x+\frac{1}{\beta_{1}}\right) \cdots\left(x+\frac{1}{\beta_{n}}\right)+\left(\overline{c_{n}}\right)^{-1} \end{aligned} $$ The equation $(\boldsymbol{\oplus})$ is the main player: Claim - We have $c_{k}=0$ for all $k=1, \ldots, n-1$. $$ \frac{c_{n-k}}{\prod_{i} \alpha_{i}}=\frac{c_{n-k}}{\prod_{i} \beta_{i}} $$ but $\prod_{i} \alpha_{i}-\prod_{i} \beta_{i}=\frac{1}{c_{n}} \neq 0$. Hence $c_{k}=0$. It follows that $P(x)$ must be of the form $P(x)=\lambda x^{n}-\mu$, so that $P(x)=\lambda x^{n}-(\mu+1)$. This requires $|\mu|=|\mu+1|=|\lambda|$ which is equivalent to the stated part.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.
|
The answer is $P(x)$ should be a polynomial of the form $P(x)=\lambda x^{n}-\mu$ where $|\lambda|=|\mu|$ and $\operatorname{Re} \mu=-\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. II Second approach (from the author). We let $A=P$ and $B=P-1$ to make the notation more symmetric. We will as before show that $A$ and $B$ have all coefficients equal to zero other than the leading and constant coefficient; the finish is the same. First, we rule out double roots. Claim - Neither $A$ nor $B$ have double roots. Let $\omega=e^{2 \pi i / n}$, let $a_{1}, \ldots, a_{n}$ be the roots of $A$, and let $b_{1}, \ldots, b_{n}$ be the roots of $B$. For each $k$, let $A_{k}$ and $B_{k}$ be the points in the complex plane corresponding to $a_{k}$ and $b_{k}$ 。 Claim (Main claim) - For any $i$ and $j, \frac{a_{i}}{a_{j}}$ is a power of $\omega$. $$ \frac{a_{i}-b_{1}}{a_{j}-b_{1}} \cdots \frac{a_{i}-b_{n}}{a_{j}-b_{n}}=\frac{B\left(a_{i}\right)}{B\left(a_{j}\right)}=\frac{A\left(a_{i}\right)-1}{A\left(a_{j}\right)-1}=\frac{0-1}{0-1}=1 $$ Since the points $A_{i}, A_{j}, B_{k}$ all lie on the unit circle, interpreting the left-hand side geometrically gives $$ \measuredangle A_{i} B_{1} A_{j}+\cdots+\measuredangle A_{i} B_{n} A_{j}=0 \Longrightarrow n \widehat{A_{i} A_{j}}=0 $$ where angles are directed modulo $180^{\circ}$ and arcs are directed modulo $360^{\circ}$. This implies that $\frac{a_{i}}{a_{j}}$ is a power of $\omega$. Now the finish is easy: since $a_{1}, \ldots, a_{n}$ are all different, they must be $a_{1} \omega^{0}, \ldots, a_{1} \omega^{n-1}$ in some order; this shows that $A$ is a multiple of $x^{n}-a_{1}^{n}$, as needed.
|
P(x)=\lambda x^{n}-\mu \text{ where } |\lambda|=|\mu| \text{ and } \operatorname{Re} \mu=-\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all nonconstant polynomials $P(z)$ with complex coefficients for which all complex roots of the polynomials $P(z)$ and $P(z)-1$ have absolute value 1.
|
The answer is $P(x)$ should be a polynomial of the form $P(x)=\lambda x^{n}-\mu$ where $|\lambda|=|\mu|$ and $\operatorname{Re} \mu=-\frac{1}{2}$. One may check these all work; let's prove they are the only solutions. II Second approach (from the author). We let $A=P$ and $B=P-1$ to make the notation more symmetric. We will as before show that $A$ and $B$ have all coefficients equal to zero other than the leading and constant coefficient; the finish is the same. First, we rule out double roots. Claim - Neither $A$ nor $B$ have double roots. Let $\omega=e^{2 \pi i / n}$, let $a_{1}, \ldots, a_{n}$ be the roots of $A$, and let $b_{1}, \ldots, b_{n}$ be the roots of $B$. For each $k$, let $A_{k}$ and $B_{k}$ be the points in the complex plane corresponding to $a_{k}$ and $b_{k}$ 。 Claim (Main claim) - For any $i$ and $j, \frac{a_{i}}{a_{j}}$ is a power of $\omega$. $$ \frac{a_{i}-b_{1}}{a_{j}-b_{1}} \cdots \frac{a_{i}-b_{n}}{a_{j}-b_{n}}=\frac{B\left(a_{i}\right)}{B\left(a_{j}\right)}=\frac{A\left(a_{i}\right)-1}{A\left(a_{j}\right)-1}=\frac{0-1}{0-1}=1 $$ Since the points $A_{i}, A_{j}, B_{k}$ all lie on the unit circle, interpreting the left-hand side geometrically gives $$ \measuredangle A_{i} B_{1} A_{j}+\cdots+\measuredangle A_{i} B_{n} A_{j}=0 \Longrightarrow n \widehat{A_{i} A_{j}}=0 $$ where angles are directed modulo $180^{\circ}$ and arcs are directed modulo $360^{\circ}$. This implies that $\frac{a_{i}}{a_{j}}$ is a power of $\omega$. Now the finish is easy: since $a_{1}, \ldots, a_{n}$ are all different, they must be $a_{1} \omega^{0}, \ldots, a_{1} \omega^{n-1}$ in some order; this shows that $A$ is a multiple of $x^{n}-a_{1}^{n}$, as needed.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
For every positive integer $N$, let $\sigma(N)$ denote the sum of the positive integer divisors of $N$. Find all integers $m \geq n \geq 2$ satisfying $$ \frac{\sigma(m)-1}{m-1}=\frac{\sigma(n)-1}{n-1}=\frac{\sigma(m n)-1}{m n-1} . $$
|
The answer is that $m$ and $n$ should be powers of the same prime number. These all work because for a prime power we have $$ \frac{\sigma\left(p^{e}\right)-1}{p^{e}-1}=\frac{\left(1+p+\cdots+p^{e}\right)-1}{p^{e}-1}=\frac{p\left(1+\cdots+p^{e-1}\right)}{p^{e}-1}=\frac{p}{p-1} $$ So we now prove these are the only ones. Let $\lambda$ be the common value of the three fractions. $$ \begin{aligned} \sigma(m n) & \geq \sigma(m)+m \sigma(n)-m \\ & =(\lambda m-\lambda+1)+m(\lambda n-\lambda+1)-m \\ & =\lambda m n-\lambda+1 \end{aligned} $$ and so equality holds. Thus these are all the divisors of $m n$, for a count of $d(m)+d(n)-$ 1. Claim - If $d(m n)=d(m)+d(n)-1$ and $\min (m, n) \geq 2$, then $m$ and $n$ are powers of the same prime. Remark (Nikolai Beluhov). Here is a completion not relying on $|A \cdot B|=|A|+|B|-1$. By the above arguments, we see that every divisor of $m n$ is either a divisor of $n$, or $n$ times a divisor of $m$. Now suppose that some prime $p \mid m$ but $p \nmid n$. Then $p \mid m n$ but $p$ does not appear in the above classification, a contradiction. By symmetry, it follows that $m$ and $n$ have the same prime divisors. Now suppose we have different primes $p \mid m$ and $q \mid n$. Write $\nu_{p}(m)=\alpha$ and $\nu_{p}(n)=\beta$. Then $p^{\alpha+\beta} \mid m n$, but it does not appear in the above characterization, a contradiction. Thus, $m$ and $n$ are powers of the same prime. Remark (Comments on the function in the problem). Let $f(n)=\frac{\sigma(n)-1}{n-1}$. Then $f$ is not really injective even outside the above solution; for example, we have $f\left(6 \cdot 11^{k}\right)=\frac{11}{5}$ for all $k$, plus sporadic equivalences like $f(14)=f(404)$, as pointed out by one reviewer during test-solving. This means that both relations should be used at once, not independently. Remark (Authorship remarks). Ankan gave the following story for how he came up with the problem while thinking about so-called almost perfect numbers. I was in some boring talk when I recalled a conjecture that if $\sigma(n)=2 n-1$, then $n$ is a power of 2 . For some reason (divine intervention, maybe) I had the double idea of (1) seeing whether $m, n, m n$ all almost perfect implies $m, n$ powers of 2 , and (2) trying the naive divisor bound to resolve this. Through sheer dumb luck this happened to work out perfectly. I thought this was kinda cool but I felt that I hadn't really unlocked a lot of the potential this idea had: then I basically tried to find the "general situation" which allows for this manipulation, and was amazed that it led to such a striking statement.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For every positive integer $N$, let $\sigma(N)$ denote the sum of the positive integer divisors of $N$. Find all integers $m \geq n \geq 2$ satisfying $$ \frac{\sigma(m)-1}{m-1}=\frac{\sigma(n)-1}{n-1}=\frac{\sigma(m n)-1}{m n-1} . $$
|
The answer is that $m$ and $n$ should be powers of the same prime number. These all work because for a prime power we have $$ \frac{\sigma\left(p^{e}\right)-1}{p^{e}-1}=\frac{\left(1+p+\cdots+p^{e}\right)-1}{p^{e}-1}=\frac{p\left(1+\cdots+p^{e-1}\right)}{p^{e}-1}=\frac{p}{p-1} $$ So we now prove these are the only ones. Let $\lambda$ be the common value of the three fractions. $$ \begin{aligned} \sigma(m n) & \geq \sigma(m)+m \sigma(n)-m \\ & =(\lambda m-\lambda+1)+m(\lambda n-\lambda+1)-m \\ & =\lambda m n-\lambda+1 \end{aligned} $$ and so equality holds. Thus these are all the divisors of $m n$, for a count of $d(m)+d(n)-$ 1. Claim - If $d(m n)=d(m)+d(n)-1$ and $\min (m, n) \geq 2$, then $m$ and $n$ are powers of the same prime. Remark (Nikolai Beluhov). Here is a completion not relying on $|A \cdot B|=|A|+|B|-1$. By the above arguments, we see that every divisor of $m n$ is either a divisor of $n$, or $n$ times a divisor of $m$. Now suppose that some prime $p \mid m$ but $p \nmid n$. Then $p \mid m n$ but $p$ does not appear in the above classification, a contradiction. By symmetry, it follows that $m$ and $n$ have the same prime divisors. Now suppose we have different primes $p \mid m$ and $q \mid n$. Write $\nu_{p}(m)=\alpha$ and $\nu_{p}(n)=\beta$. Then $p^{\alpha+\beta} \mid m n$, but it does not appear in the above characterization, a contradiction. Thus, $m$ and $n$ are powers of the same prime. Remark (Comments on the function in the problem). Let $f(n)=\frac{\sigma(n)-1}{n-1}$. Then $f$ is not really injective even outside the above solution; for example, we have $f\left(6 \cdot 11^{k}\right)=\frac{11}{5}$ for all $k$, plus sporadic equivalences like $f(14)=f(404)$, as pointed out by one reviewer during test-solving. This means that both relations should be used at once, not independently. Remark (Authorship remarks). Ankan gave the following story for how he came up with the problem while thinking about so-called almost perfect numbers. I was in some boring talk when I recalled a conjecture that if $\sigma(n)=2 n-1$, then $n$ is a power of 2 . For some reason (divine intervention, maybe) I had the double idea of (1) seeing whether $m, n, m n$ all almost perfect implies $m, n$ powers of 2 , and (2) trying the naive divisor bound to resolve this. Through sheer dumb luck this happened to work out perfectly. I thought this was kinda cool but I felt that I hadn't really unlocked a lot of the potential this idea had: then I basically tried to find the "general situation" which allows for this manipulation, and was amazed that it led to such a striking statement.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Ten million fireflies are glowing in $\mathbb{R}^{3}$ at midnight. Some of the fireflies are friends, and friendship is always mutual. Every second, one firefly moves to a new position so that its distance from each one of its friends is the same as it was before moving. This is the only way that the fireflies ever change their positions. No two fireflies may ever occupy the same point. Initially, no two fireflies, friends or not, are more than a meter away. Following some finite number of seconds, all fireflies find themselves at least ten million meters away from their original positions. Given this information, find the greatest possible number of friendships between the fireflies.
|
In general, we show that when $n \geq 70$, the answer is $f(n)=\left\lfloor\frac{n^{2}}{3}\right\rfloor$. Construction: Choose three pairwise parallel lines $\ell_{A}, \ell_{B}, \ell_{C}$ forming an infinite equilateral triangle prism (with side larger than 1). Split the $n$ fireflies among the lines as equally as possible, and say that two fireflies are friends iff they lie on different lines. To see this works: 1. Reflect $\ell_{A}$ and all fireflies on $\ell_{A}$ in the plane containing $\ell_{B}$ and $\ell_{C}$. 2. Reflect $\ell_{B}$ and all fireflies on $\ell_{B}$ in the plane containing $\ell_{C}$ and $\ell_{A}$. 3. Reflect $\ell_{C}$ and all fireflies on $\ell_{C}$ in the plane containing $\ell_{A}$ and $\ell_{B}$. Let $g(n)$ be the answer, given that there exist four pairwise friends (say $a, b, c, d$ ). Note that for a firefly to move, all its friends must be coplanar. Claim (No coplanar $K_{4}$ ) — We can't have four coplanar fireflies which are pairwise friends. Claim (Key claim — tetrahedrons don't share faces often) — There are at most 12 fireflies $e$ which are friends with at least three of $a, b, c, d$. WLOG, will assume that $e$ is friends with $a, b, c$. Then $e$ will always be located at one of two points $E_{1}$ and $E_{2}$ relative to $A B C$, such that $E_{1} A B C$ and $E_{2} A B C$ are two congruent tetrahedrons with fixed shape. We note that points $D, E_{1}$, and $E_{2}$ are all different: clearly $D \neq E_{1}$ and $E_{1} \neq E_{2}$. (If $D=E_{2}$, then some fireflies won't be able to move.) Consider the moment where firefly $a$ moves. Its friends must be coplanar at that time, so one of $E_{1}, E_{2}$ lies in plane $B C D$. Similar reasoning holds for planes $A C D$ and $A B D$. So, WLOG $E_{1}$ lies on both planes $B C D$ and $A C D$. Then $E_{1}$ lies on line $C D$, and $E_{2}$ lies in plane $A B D$. This uniquely determines $\left(E_{1}, E_{2}\right)$ relative to $A B C D$ : - $E_{1}$ is the intersection of line $C D$ with the reflection of plane $A B D$ in plane $A B C$. - $E_{2}$ is the intersection of plane $A B D$ with the reflection of line $C D$ in plane $A B C$. Accounting for WLOGs, there are at most 12 possibilities for the set $\left\{E_{1}, E_{2}\right\}$, and thus at most 12 possibilities for $E$. (It's not possible for both elements of one pair $\left\{E_{1}, E_{2}\right\}$ to be occupied, because then they couldn't move.) Thus, the number of friendships involving exactly one of $a, b, c, d$ is at most $(n-16)$. $2+12 \cdot 3=2 n+4$, so removing these four fireflies gives $$ g(n) \leq 6+(2 n+4)+\max \{f(n-4), g(n-4)\} $$ $$ g(n) \leq \max \{f(n),(2 n+10)+g(n-4)\} \quad \forall n \geq 24 $$ By iterating the above inequality, we get $$ \begin{aligned} g(n) \leq \max \{f(n),(2 n+10) & +(2(n-4)+10) \\ & +\cdots+(2(n-4 r)+10)+g(n-4 r-4)\} \end{aligned} $$ where $r$ satisfies $n-4 r-4<24 \leq n-4 r$. Now $$ \begin{aligned} & (2 n+10)+(2(n-4)+10)+\cdots+(2(n-4 r)+10)+g(n-4 r-4) \\ = & (r+1)(2 n-4 r+10)+g(n-4 r-4) \\ \leq & \left(\frac{n}{4}-5\right)(n+37)+\binom{24}{2} . \end{aligned} $$ This is less than $f(n)$ for $n \geq 70$, which concludes the solution. Remark. There are positive integers $n$ such that it is possible to do better than $f(n)$ friendships. For instance, $f(5)=8$, whereas five fireflies $a, b, c, d$, and $e$ as in the proof of the Lemma ( $E_{1}$ being the intersection point of line $C D$ with the reflection of plane $(A B D)$ in plane $(A B C), E_{2}$ being the intersection point of plane $(A B D)$ with the reflection of line $C D$ in plane $(A B C)$, and tetrahedron $A B C D$ being sufficiently arbitrary that points $E_{1}$ and $E_{2}$ exist and points $D, E_{1}$, and $E_{2}$ are pairwise distinct) give a total of nine friendships. Remark (Author comments). It is natural to approach the problem by looking at the two-dimensional version first. In two dimensions, the following arrangement suggests itself almost immediately: We distribute all fireflies as equally as possible among two parallel lines, and two fireflies are friends if and only if they are on different lines. Similarly to the three-dimensional version, this attains the greatest possible number of friendships for all sufficiently large $n$, though not for all $n$. For instance, at least one friendlier arrangements exists for $n=4$, similarly to the above friendlier arrangement for $n=5$ in three dimensions. This observation strongly suggests that in three dimensions we should distribute the fireflies as equally as possible among two parallel planes, and that two fireflies should be friends if and only if they are on different planes. It was a great surprise for me to discover that this arrangement does not in fact give the correct answer! Remark. On the other hand, Ankan Bhattacharya gives the following reasoning as to why the answer should not be that surprising: I think the answer $\left(10^{14}-1\right) / 3$ is quite natural if you realize that $(n / 2)^{2}$ is probably optimal in 2D and $\binom{n}{2}$ is optimal in super high dimensions (i.e. around $n$ ). So going from dimension 2 to 3 should increase the answer (and indeed it does).
|
\left\lfloor\frac{n^{2}}{3}\right\rfloor
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Ten million fireflies are glowing in $\mathbb{R}^{3}$ at midnight. Some of the fireflies are friends, and friendship is always mutual. Every second, one firefly moves to a new position so that its distance from each one of its friends is the same as it was before moving. This is the only way that the fireflies ever change their positions. No two fireflies may ever occupy the same point. Initially, no two fireflies, friends or not, are more than a meter away. Following some finite number of seconds, all fireflies find themselves at least ten million meters away from their original positions. Given this information, find the greatest possible number of friendships between the fireflies.
|
In general, we show that when $n \geq 70$, the answer is $f(n)=\left\lfloor\frac{n^{2}}{3}\right\rfloor$. Construction: Choose three pairwise parallel lines $\ell_{A}, \ell_{B}, \ell_{C}$ forming an infinite equilateral triangle prism (with side larger than 1). Split the $n$ fireflies among the lines as equally as possible, and say that two fireflies are friends iff they lie on different lines. To see this works: 1. Reflect $\ell_{A}$ and all fireflies on $\ell_{A}$ in the plane containing $\ell_{B}$ and $\ell_{C}$. 2. Reflect $\ell_{B}$ and all fireflies on $\ell_{B}$ in the plane containing $\ell_{C}$ and $\ell_{A}$. 3. Reflect $\ell_{C}$ and all fireflies on $\ell_{C}$ in the plane containing $\ell_{A}$ and $\ell_{B}$. Let $g(n)$ be the answer, given that there exist four pairwise friends (say $a, b, c, d$ ). Note that for a firefly to move, all its friends must be coplanar. Claim (No coplanar $K_{4}$ ) — We can't have four coplanar fireflies which are pairwise friends. Claim (Key claim — tetrahedrons don't share faces often) — There are at most 12 fireflies $e$ which are friends with at least three of $a, b, c, d$. WLOG, will assume that $e$ is friends with $a, b, c$. Then $e$ will always be located at one of two points $E_{1}$ and $E_{2}$ relative to $A B C$, such that $E_{1} A B C$ and $E_{2} A B C$ are two congruent tetrahedrons with fixed shape. We note that points $D, E_{1}$, and $E_{2}$ are all different: clearly $D \neq E_{1}$ and $E_{1} \neq E_{2}$. (If $D=E_{2}$, then some fireflies won't be able to move.) Consider the moment where firefly $a$ moves. Its friends must be coplanar at that time, so one of $E_{1}, E_{2}$ lies in plane $B C D$. Similar reasoning holds for planes $A C D$ and $A B D$. So, WLOG $E_{1}$ lies on both planes $B C D$ and $A C D$. Then $E_{1}$ lies on line $C D$, and $E_{2}$ lies in plane $A B D$. This uniquely determines $\left(E_{1}, E_{2}\right)$ relative to $A B C D$ : - $E_{1}$ is the intersection of line $C D$ with the reflection of plane $A B D$ in plane $A B C$. - $E_{2}$ is the intersection of plane $A B D$ with the reflection of line $C D$ in plane $A B C$. Accounting for WLOGs, there are at most 12 possibilities for the set $\left\{E_{1}, E_{2}\right\}$, and thus at most 12 possibilities for $E$. (It's not possible for both elements of one pair $\left\{E_{1}, E_{2}\right\}$ to be occupied, because then they couldn't move.) Thus, the number of friendships involving exactly one of $a, b, c, d$ is at most $(n-16)$. $2+12 \cdot 3=2 n+4$, so removing these four fireflies gives $$ g(n) \leq 6+(2 n+4)+\max \{f(n-4), g(n-4)\} $$ $$ g(n) \leq \max \{f(n),(2 n+10)+g(n-4)\} \quad \forall n \geq 24 $$ By iterating the above inequality, we get $$ \begin{aligned} g(n) \leq \max \{f(n),(2 n+10) & +(2(n-4)+10) \\ & +\cdots+(2(n-4 r)+10)+g(n-4 r-4)\} \end{aligned} $$ where $r$ satisfies $n-4 r-4<24 \leq n-4 r$. Now $$ \begin{aligned} & (2 n+10)+(2(n-4)+10)+\cdots+(2(n-4 r)+10)+g(n-4 r-4) \\ = & (r+1)(2 n-4 r+10)+g(n-4 r-4) \\ \leq & \left(\frac{n}{4}-5\right)(n+37)+\binom{24}{2} . \end{aligned} $$ This is less than $f(n)$ for $n \geq 70$, which concludes the solution. Remark. There are positive integers $n$ such that it is possible to do better than $f(n)$ friendships. For instance, $f(5)=8$, whereas five fireflies $a, b, c, d$, and $e$ as in the proof of the Lemma ( $E_{1}$ being the intersection point of line $C D$ with the reflection of plane $(A B D)$ in plane $(A B C), E_{2}$ being the intersection point of plane $(A B D)$ with the reflection of line $C D$ in plane $(A B C)$, and tetrahedron $A B C D$ being sufficiently arbitrary that points $E_{1}$ and $E_{2}$ exist and points $D, E_{1}$, and $E_{2}$ are pairwise distinct) give a total of nine friendships. Remark (Author comments). It is natural to approach the problem by looking at the two-dimensional version first. In two dimensions, the following arrangement suggests itself almost immediately: We distribute all fireflies as equally as possible among two parallel lines, and two fireflies are friends if and only if they are on different lines. Similarly to the three-dimensional version, this attains the greatest possible number of friendships for all sufficiently large $n$, though not for all $n$. For instance, at least one friendlier arrangements exists for $n=4$, similarly to the above friendlier arrangement for $n=5$ in three dimensions. This observation strongly suggests that in three dimensions we should distribute the fireflies as equally as possible among two parallel planes, and that two fireflies should be friends if and only if they are on different planes. It was a great surprise for me to discover that this arrangement does not in fact give the correct answer! Remark. On the other hand, Ankan Bhattacharya gives the following reasoning as to why the answer should not be that surprising: I think the answer $\left(10^{14}-1\right) / 3$ is quite natural if you realize that $(n / 2)^{2}$ is probably optimal in 2D and $\binom{n}{2}$ is optimal in super high dimensions (i.e. around $n$ ). So going from dimension 2 to 3 should increase the answer (and indeed it does).
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2020"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\prime}$ and $B^{\prime}$, respectively. 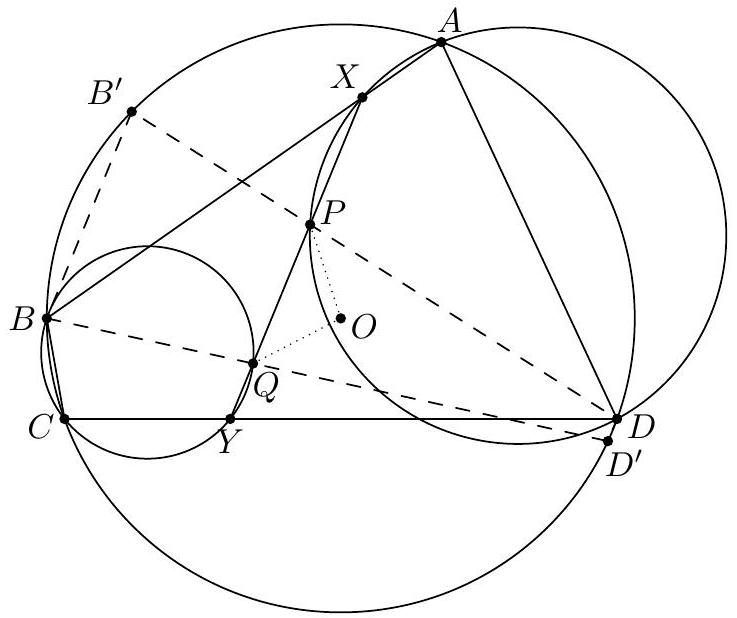 Then $B B^{\prime} \| P X$ and $D D^{\prime} \| Q Y$ by Reim's theorem. Segments $B B^{\prime}, D D^{\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\prime}$ and $B^{\prime}$, respectively.  Then $B B^{\prime} \| P X$ and $D D^{\prime} \| Q Y$ by Reim's theorem. Segments $B B^{\prime}, D D^{\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Second solution via isosceles triangles (from contestants). Let $T=\overline{B Q} \cap \overline{D P}$. 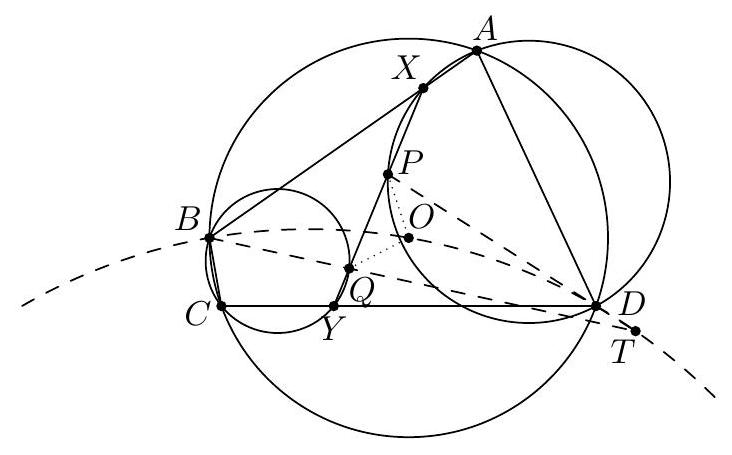 Note that $P Q T$ is isosceles because $$ \measuredangle P Q T=\measuredangle Y Q B=\measuredangle B C D=\measuredangle B A D=\measuredangle X P D=\measuredangle T P Q $$ Then $(B O D T)$ is cyclic because $$ \measuredangle B O D=2 \measuredangle B C D=\measuredangle P Q T+\measuredangle T P Q=\measuredangle B T D . $$ Since $B O=O D, \overline{T O}$ is an angle bisector of $\measuredangle B T D$. Since $\triangle P Q T$ is isosceles, $\overline{T O} \perp \overline{P Q}$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Second solution via isosceles triangles (from contestants). Let $T=\overline{B Q} \cap \overline{D P}$.  Note that $P Q T$ is isosceles because $$ \measuredangle P Q T=\measuredangle Y Q B=\measuredangle B C D=\measuredangle B A D=\measuredangle X P D=\measuredangle T P Q $$ Then $(B O D T)$ is cyclic because $$ \measuredangle B O D=2 \measuredangle B C D=\measuredangle P Q T+\measuredangle T P Q=\measuredangle B T D . $$ Since $B O=O D, \overline{T O}$ is an angle bisector of $\measuredangle B T D$. Since $\triangle P Q T$ is isosceles, $\overline{T O} \perp \overline{P Q}$, so $O P=O Q$.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\overline{A B}$ again at $W$ and let $(A D X)$ meet $\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$. 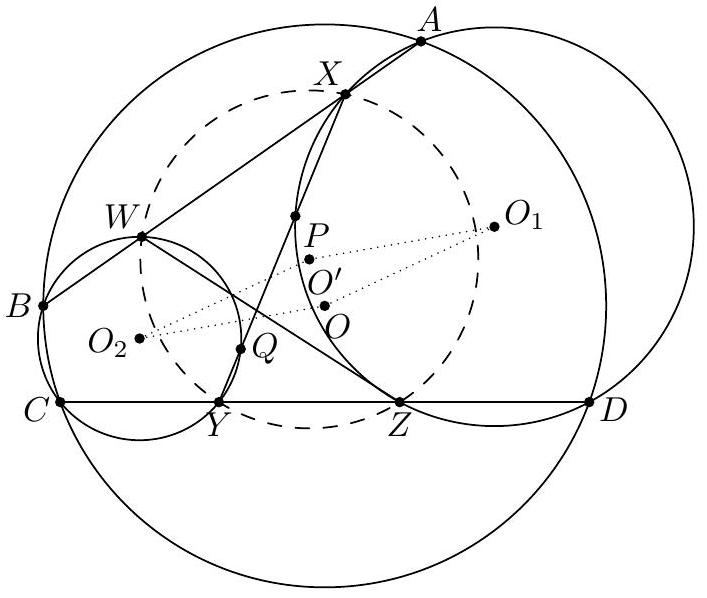 Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ so let $O^{\prime}$ be the center of ( $W X Y Z$ ). Since $\overline{A D} \| \overline{W Y}$ and $\overline{B C} \| \overline{X Z}$ by Reim's theorem, $O O_{1} O^{\prime} O_{2}$ is a parallelogram. To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\prime}$ onto $\overline{X Y}$ gives the midpoints of $\overline{P X}, \overline{Q Y}$, and $\overline{X Y}$. Since $O O_{1} O^{\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\overline{X Y}$ must give the midpoint of $\overline{P Q}$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\overline{A B}$ again at $W$ and let $(A D X)$ meet $\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$.  Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ so let $O^{\prime}$ be the center of ( $W X Y Z$ ). Since $\overline{A D} \| \overline{W Y}$ and $\overline{B C} \| \overline{X Z}$ by Reim's theorem, $O O_{1} O^{\prime} O_{2}$ is a parallelogram. To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\prime}$ onto $\overline{X Y}$ gives the midpoints of $\overline{P X}, \overline{Q Y}$, and $\overline{X Y}$. Since $O O_{1} O^{\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\overline{X Y}$ must give the midpoint of $\overline{P Q}$, so $O P=O Q$.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\measuredangle B O D$ meet $\overline{X Y}$ at $K$. 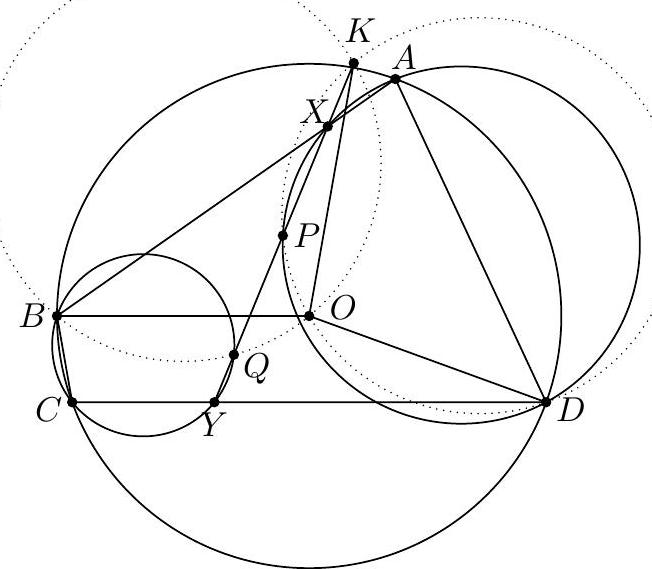 Then $(B Q O K)$ is cyclic because $\measuredangle K O D=\measuredangle B A D=\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so $$ O P=2 r \sin \angle O K P=2 r \sin \angle O K Q=O Q $$ by the Law of Sines.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\measuredangle B O D$ meet $\overline{X Y}$ at $K$.  Then $(B Q O K)$ is cyclic because $\measuredangle K O D=\measuredangle B A D=\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so $$ O P=2 r \sin \angle O K P=2 r \sin \angle O K Q=O Q $$ by the Law of Sines.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Fifth solution by ratio calculation (from contestants). Let $\overline{X Y}$ meet $(A B C D)$ at $X^{\prime}$ and $Y^{\prime}$. 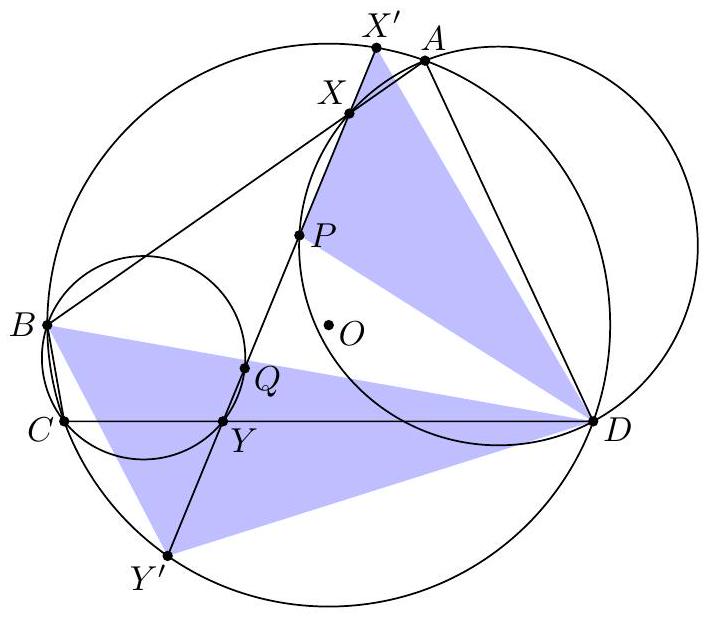 Since $\measuredangle Y^{\prime} B D=\measuredangle P X^{\prime} D$ and $\measuredangle B Y^{\prime} D=\measuredangle B A D=\measuredangle X^{\prime} P D$, $$ \triangle B Y^{\prime} D \sim \triangle X P^{\prime} D \Longrightarrow P X^{\prime}=B Y^{\prime} \cdot \frac{D X^{\prime}}{B D} $$ Similarly, $$ \triangle B X^{\prime} D \sim \triangle B Q Y^{\prime} \Longrightarrow Q Y^{\prime}=D X^{\prime} \cdot \frac{B Y^{\prime}}{B D} $$ Thus $P X^{\prime}=Q Y^{\prime}$, which gives $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Fifth solution by ratio calculation (from contestants). Let $\overline{X Y}$ meet $(A B C D)$ at $X^{\prime}$ and $Y^{\prime}$.  Since $\measuredangle Y^{\prime} B D=\measuredangle P X^{\prime} D$ and $\measuredangle B Y^{\prime} D=\measuredangle B A D=\measuredangle X^{\prime} P D$, $$ \triangle B Y^{\prime} D \sim \triangle X P^{\prime} D \Longrightarrow P X^{\prime}=B Y^{\prime} \cdot \frac{D X^{\prime}}{B D} $$ Similarly, $$ \triangle B X^{\prime} D \sim \triangle B Q Y^{\prime} \Longrightarrow Q Y^{\prime}=D X^{\prime} \cdot \frac{B Y^{\prime}}{B D} $$ Thus $P X^{\prime}=Q Y^{\prime}$, which gives $O P=O Q$.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
I Sixth solution using radical axis (from author). Without loss of generality, assume $\overline{A D} \nVdash \overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\overline{A B}$ again at $W$, let $(A D X)$ meet $\overline{C D}$ again at $Z$, and let $\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$. 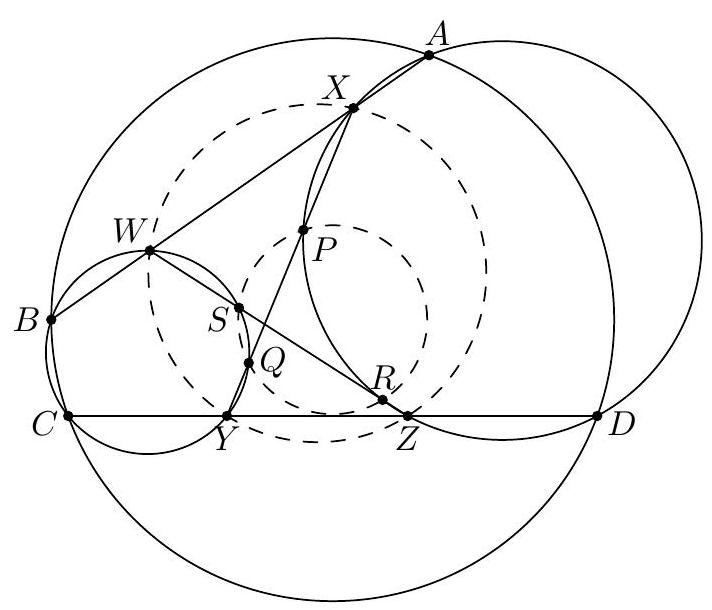 Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ and $(P Q R S)$ is cyclic since $$ \measuredangle P Q S=\measuredangle Y Q S=\measuredangle Y W S=\measuredangle P X Z=\measuredangle P R Z=\measuredangle S R P $$ Additionally, $\overline{A D} \| \overline{P R}$ since $$ \measuredangle D A X+\measuredangle A X P+\measuredangle X P R=\measuredangle Y W X+\measuredangle W X Y+\measuredangle X Y W=0^{\circ}, $$ and $\overline{B C} \| \overline{S Q}$ similarly. Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\overline{A D}$ and $\overline{B C}$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
I Sixth solution using radical axis (from author). Without loss of generality, assume $\overline{A D} \nVdash \overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\overline{A B}$ again at $W$, let $(A D X)$ meet $\overline{C D}$ again at $Z$, and let $\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$.  Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ and $(P Q R S)$ is cyclic since $$ \measuredangle P Q S=\measuredangle Y Q S=\measuredangle Y W S=\measuredangle P X Z=\measuredangle P R Z=\measuredangle S R P $$ Additionally, $\overline{A D} \| \overline{P R}$ since $$ \measuredangle D A X+\measuredangle A X P+\measuredangle X P R=\measuredangle Y W X+\measuredangle W X Y+\measuredangle X Y W=0^{\circ}, $$ and $\overline{B C} \| \overline{S Q}$ similarly. Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\overline{A D}$ and $\overline{B C}$, contradiction.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution. 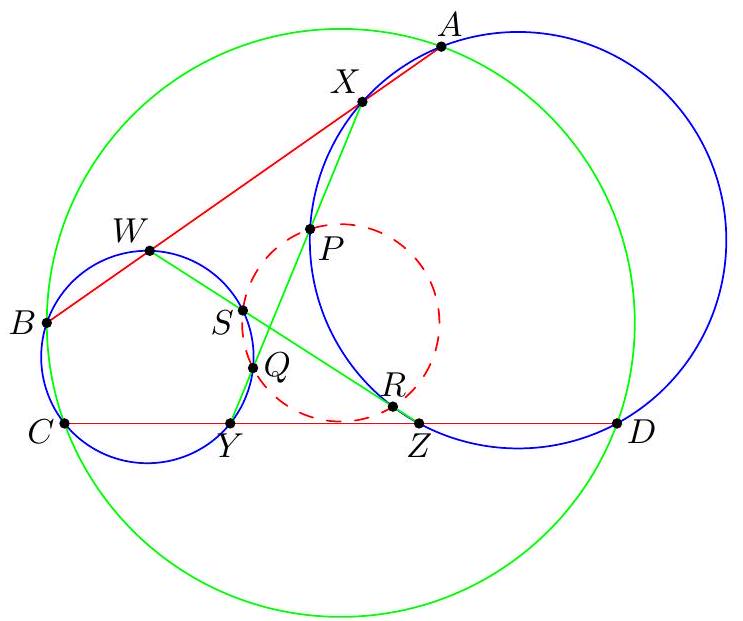 The quartics $(A D X Z) \cup(B C W Y)$ and $\overline{X Y} \cup \overline{W Z} \cup(A B C D)$ meet at the 16 points $$ A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J $$ where $I$ and $J$ are the circular points at infinity. Since $\overline{A B} \cup \overline{C D} \cup(P Q R)$ contains the 13 points $$ A, B, C, D, P, Q, R, W, X, Y, Z, I, J $$ it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired. Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution.  The quartics $(A D X Z) \cup(B C W Y)$ and $\overline{X Y} \cup \overline{W Z} \cup(A B C D)$ meet at the 16 points $$ A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J $$ where $I$ and $J$ are the circular points at infinity. Since $\overline{A B} \cup \overline{C D} \cup(P Q R)$ contains the 13 points $$ A, B, C, D, P, Q, R, W, X, Y, Z, I, J $$ it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired. Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\lambda$ for which the set $S_{\lambda}=\left\{k: a_{k} / k=\lambda\right\}$ is non-empty, it contains at least two elements. Note that $S_{\lambda}$ is always a finite set because $a_{k}=k \lambda$ implies $k<1 / \lambda$. Write $m_{\lambda}$ and $M_{\lambda}$ for the smallest and largest element of $S_{\lambda}$, respectively, and define $T_{\lambda}=\left\{m_{\lambda}, m_{\lambda}+1, \ldots, M_{\lambda}\right\}$ as the smallest set of consecutive positive integers that contains $S_{\lambda}$. Then all $T_{\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\lambda}$ cover $\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\lambda}$ smaller than any fixed integer. Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\lambda}$, we may throw out one set while maintaining the property that the $T_{\lambda}$ cover $\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice. Let $\Lambda$ denote the set of the $\lambda$-values for which $T_{\lambda}$ remains in our collection of sets; then $\bigcup_{\lambda \in \Lambda} T_{\lambda}=\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\lambda}$. We now obtain $$ \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \leq 2 \sum_{k \geq 1}\left(a_{k+1}-a_{k}\right) \leq 2 $$ On the other hand, because $a_{m_{\lambda}}=\lambda m_{\lambda}$ and $a_{M_{\lambda}}=\lambda M_{\lambda}$, we have $$ \begin{aligned} 2 \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) & \geq 2 \sum_{m_{\lambda} \leq k<M_{\lambda}}\left(a_{k+1}-a_{k}\right)=2\left(a_{M_{\lambda}}-a_{m_{\lambda}}\right)=2\left(M_{\lambda}-m_{\lambda}\right) \lambda \\ & =2\left(M_{\lambda}-m_{\lambda}\right) \cdot \frac{a_{m_{\lambda}}}{m_{\lambda}} \geq\left(M_{\lambda}-m_{\lambda}+1\right) \cdot \frac{a_{1}}{m_{\lambda}} \geq a_{1} \cdot \sum_{k \in T_{\lambda}} \frac{1}{k} . \end{aligned} $$ Combining this with our first estimate, and using the fact that the $T_{\lambda}$ cover $\mathbb{N}$, we obtain $$ 4 \geq 2 \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \geq a_{1} \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}} \frac{1}{k} \geq a_{1} \sum_{k \geq 1} \frac{1}{k} $$ contradicting the fact that the harmonic series diverges.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\lambda$ for which the set $S_{\lambda}=\left\{k: a_{k} / k=\lambda\right\}$ is non-empty, it contains at least two elements. Note that $S_{\lambda}$ is always a finite set because $a_{k}=k \lambda$ implies $k<1 / \lambda$. Write $m_{\lambda}$ and $M_{\lambda}$ for the smallest and largest element of $S_{\lambda}$, respectively, and define $T_{\lambda}=\left\{m_{\lambda}, m_{\lambda}+1, \ldots, M_{\lambda}\right\}$ as the smallest set of consecutive positive integers that contains $S_{\lambda}$. Then all $T_{\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\lambda}$ cover $\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\lambda}$ smaller than any fixed integer. Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\lambda}$, we may throw out one set while maintaining the property that the $T_{\lambda}$ cover $\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice. Let $\Lambda$ denote the set of the $\lambda$-values for which $T_{\lambda}$ remains in our collection of sets; then $\bigcup_{\lambda \in \Lambda} T_{\lambda}=\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\lambda}$. We now obtain $$ \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \leq 2 \sum_{k \geq 1}\left(a_{k+1}-a_{k}\right) \leq 2 $$ On the other hand, because $a_{m_{\lambda}}=\lambda m_{\lambda}$ and $a_{M_{\lambda}}=\lambda M_{\lambda}$, we have $$ \begin{aligned} 2 \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) & \geq 2 \sum_{m_{\lambda} \leq k<M_{\lambda}}\left(a_{k+1}-a_{k}\right)=2\left(a_{M_{\lambda}}-a_{m_{\lambda}}\right)=2\left(M_{\lambda}-m_{\lambda}\right) \lambda \\ & =2\left(M_{\lambda}-m_{\lambda}\right) \cdot \frac{a_{m_{\lambda}}}{m_{\lambda}} \geq\left(M_{\lambda}-m_{\lambda}+1\right) \cdot \frac{a_{1}}{m_{\lambda}} \geq a_{1} \cdot \sum_{k \in T_{\lambda}} \frac{1}{k} . \end{aligned} $$ Combining this with our first estimate, and using the fact that the $T_{\lambda}$ cover $\mathbb{N}$, we obtain $$ 4 \geq 2 \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \geq a_{1} \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}} \frac{1}{k} \geq a_{1} \sum_{k \geq 1} \frac{1}{k} $$ contradicting the fact that the harmonic series diverges.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$. First, each $i$ has finite degree - otherwise $$ \frac{a_{x_{1}}}{x_{1}}=\frac{a_{x_{2}}}{x_{2}}=\cdots $$ for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded. Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound: - Start at $x_{1}=1$, which is good. - If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.) - Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \leq x \leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well. Then $x_{i}=1+s_{1}+t_{1}+\cdots+s_{i-1}+t_{i-1}$, and we have $$ a_{x_{i+1}}>a_{x_{i}+s_{i}}=\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} a_{x_{i}} $$ This means $$ c_{n}:=\frac{a_{x_{n}}}{a_{1}}>\prod_{i=1}^{n-1} \frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} $$ ## Lemma $t_{1}+\cdots+t_{n} \leq s_{1}+\cdots+s_{n}$ for each $n$. First we claim that if $x \in\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \leq i$. This is because $x>x_{i}+s_{i} \geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$. This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \leq i$, since if it did, it would have an edge to $x_{j}$. Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$. Then each of the $\sum\left(t_{i}-1\right)$ values in the intervals $\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$ for $1 \leq i \leq n$ must have an edge to an unique $y$ in one of the intervals $\left(x_{i}, x_{i}+s_{i}\right)$ (not necessarily with the same $i$ ). Therefore $$ \sum\left(t_{i}-1\right) \leq \sum\left(s_{i}-1\right) \Longrightarrow \sum t_{i} \leq \sum s_{i} $$ Now note that if $a>b$, then $\frac{a+x}{b+x}=1+\frac{a-b}{b+x}$ is decreasing in $x$. This means $$ c_{n}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}} $$ By multiplying both products, we have a telescoping product, which results in $$ c_{n}^{2} \geq 1+2 s_{1}+\cdots+2 s_{n}+2 s_{n+1} $$ The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$. First, each $i$ has finite degree - otherwise $$ \frac{a_{x_{1}}}{x_{1}}=\frac{a_{x_{2}}}{x_{2}}=\cdots $$ for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded. Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound: - Start at $x_{1}=1$, which is good. - If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.) - Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \leq x \leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well. Then $x_{i}=1+s_{1}+t_{1}+\cdots+s_{i-1}+t_{i-1}$, and we have $$ a_{x_{i+1}}>a_{x_{i}+s_{i}}=\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} a_{x_{i}} $$ This means $$ c_{n}:=\frac{a_{x_{n}}}{a_{1}}>\prod_{i=1}^{n-1} \frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} $$ ## Lemma $t_{1}+\cdots+t_{n} \leq s_{1}+\cdots+s_{n}$ for each $n$. First we claim that if $x \in\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \leq i$. This is because $x>x_{i}+s_{i} \geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$. This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \leq i$, since if it did, it would have an edge to $x_{j}$. Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$. Then each of the $\sum\left(t_{i}-1\right)$ values in the intervals $\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$ for $1 \leq i \leq n$ must have an edge to an unique $y$ in one of the intervals $\left(x_{i}, x_{i}+s_{i}\right)$ (not necessarily with the same $i$ ). Therefore $$ \sum\left(t_{i}-1\right) \leq \sum\left(s_{i}-1\right) \Longrightarrow \sum t_{i} \leq \sum s_{i} $$ Now note that if $a>b$, then $\frac{a+x}{b+x}=1+\frac{a-b}{b+x}$ is decreasing in $x$. This means $$ c_{n}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}} $$ By multiplying both products, we have a telescoping product, which results in $$ c_{n}^{2} \geq 1+2 s_{1}+\cdots+2 s_{n}+2 s_{n+1} $$ The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if $$ \frac{a_{j}}{j}=\frac{a_{i}}{i} \Longrightarrow j \geq i $$ ## Lemma There exists $k$ such that if we have $\frac{a_{i}}{i}=\frac{a_{j}}{j}$ with $j>i \geq k$, then $j \leq 1.1 i$. Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\frac{a_{j_{1}}}{j_{1}}=\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \geq i_{1}$ such that $\frac{a_{j_{2}}}{j_{2}}=\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that $$ a_{j_{\ell}}>1.1 a_{i_{\ell}}>1.1 a_{j_{\ell-1}} $$ so we have that $a_{j_{\ell}}>1.1^{\ell} a_{i_{1}}$. Taking $\ell>\log _{1.1}\left(1 / a_{1}\right)$ gives the desired contradiction. ## Lemma For $N>k^{2}$, there are at most $0.8 N$ pins in $[\sqrt{N}, N)$. $$ p-N\left(1-\frac{1}{1.1}\right) \leq N-p $$ so $p \leq 0.8 N$, as desired. We say that $i$ is the pin of $j$ if it is the smallest index such that $\frac{a_{i}}{i}=\frac{a_{j}}{j}$. The pin of $j$ is always a pin. Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\left(\sqrt{N_{0}}\right)>k$. Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\left(b_{2 i-1}\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$. Let $\ell$ be the largest odd index such that $b_{\ell} \geq \sqrt{N}$. We first show that $b_{\ell} \leq 100 \sqrt{N}$. Since $N>N_{0}$, we have $b_{\ell+1}>k$. By the choice of $\ell$ we have $b_{\ell+2}<\sqrt{N}$, so $$ b_{\ell+1}<1.1 b_{\ell+2}<1.1 \sqrt{N} $$ by the first lemma. We see that all the indices from $b_{\ell+1}+1$ to $b_{\ell}$ must be pins, so we have at least $b_{\ell}-1.1 \sqrt{N}$ pins in $\left[\sqrt{N}, b_{\ell}\right)$. Combined with the second lemma, this shows that $b_{\ell} \leq 100 \sqrt{N}$. Now, we have that $a_{b_{2 i}}=\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us $$ \frac{a_{b_{0}}}{a_{b_{\ell}}}>\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} . $$ Note that there are at least $$ \left(b_{1}-b_{2}\right)+\left(b_{3}-b_{4}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right) $$ pins in $[\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus, $$ \begin{aligned} \left(b_{0}-b_{1}\right)+\left(b_{2}-b_{3}\right)+\cdots+\left(b_{\ell-1}-b_{\ell}\right) & =b_{0}-\left[\left(b_{1}-b_{2}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)\right]-b_{\ell} \\ & \geq 0.2 N-100 \sqrt{N} . \end{aligned} $$ Then $$ \begin{aligned} \frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} & \geq 1+\frac{b_{0}-b_{1}}{b_{1}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{\ell}} \\ & >1+\frac{b_{0}-b_{1}}{b_{0}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{0}} \\ & \geq 1+\frac{0.2 N-100 \sqrt{N}}{N} \end{aligned} $$ which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that $$ a_{N}>1.01 a_{b_{\ell}} \geq 1.01 a_{\lfloor\sqrt{N}\rfloor} $$ if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\left(a_{n}\right)$ is unbounded, which is the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if $$ \frac{a_{j}}{j}=\frac{a_{i}}{i} \Longrightarrow j \geq i $$ ## Lemma There exists $k$ such that if we have $\frac{a_{i}}{i}=\frac{a_{j}}{j}$ with $j>i \geq k$, then $j \leq 1.1 i$. Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\frac{a_{j_{1}}}{j_{1}}=\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \geq i_{1}$ such that $\frac{a_{j_{2}}}{j_{2}}=\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that $$ a_{j_{\ell}}>1.1 a_{i_{\ell}}>1.1 a_{j_{\ell-1}} $$ so we have that $a_{j_{\ell}}>1.1^{\ell} a_{i_{1}}$. Taking $\ell>\log _{1.1}\left(1 / a_{1}\right)$ gives the desired contradiction. ## Lemma For $N>k^{2}$, there are at most $0.8 N$ pins in $[\sqrt{N}, N)$. $$ p-N\left(1-\frac{1}{1.1}\right) \leq N-p $$ so $p \leq 0.8 N$, as desired. We say that $i$ is the pin of $j$ if it is the smallest index such that $\frac{a_{i}}{i}=\frac{a_{j}}{j}$. The pin of $j$ is always a pin. Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\left(\sqrt{N_{0}}\right)>k$. Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\left(b_{2 i-1}\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$. Let $\ell$ be the largest odd index such that $b_{\ell} \geq \sqrt{N}$. We first show that $b_{\ell} \leq 100 \sqrt{N}$. Since $N>N_{0}$, we have $b_{\ell+1}>k$. By the choice of $\ell$ we have $b_{\ell+2}<\sqrt{N}$, so $$ b_{\ell+1}<1.1 b_{\ell+2}<1.1 \sqrt{N} $$ by the first lemma. We see that all the indices from $b_{\ell+1}+1$ to $b_{\ell}$ must be pins, so we have at least $b_{\ell}-1.1 \sqrt{N}$ pins in $\left[\sqrt{N}, b_{\ell}\right)$. Combined with the second lemma, this shows that $b_{\ell} \leq 100 \sqrt{N}$. Now, we have that $a_{b_{2 i}}=\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us $$ \frac{a_{b_{0}}}{a_{b_{\ell}}}>\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} . $$ Note that there are at least $$ \left(b_{1}-b_{2}\right)+\left(b_{3}-b_{4}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right) $$ pins in $[\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus, $$ \begin{aligned} \left(b_{0}-b_{1}\right)+\left(b_{2}-b_{3}\right)+\cdots+\left(b_{\ell-1}-b_{\ell}\right) & =b_{0}-\left[\left(b_{1}-b_{2}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)\right]-b_{\ell} \\ & \geq 0.2 N-100 \sqrt{N} . \end{aligned} $$ Then $$ \begin{aligned} \frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} & \geq 1+\frac{b_{0}-b_{1}}{b_{1}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{\ell}} \\ & >1+\frac{b_{0}-b_{1}}{b_{0}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{0}} \\ & \geq 1+\frac{0.2 N-100 \sqrt{N}}{N} \end{aligned} $$ which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that $$ a_{N}>1.01 a_{b_{\ell}} \geq 1.01 a_{\lfloor\sqrt{N}\rfloor} $$ if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\left(a_{n}\right)$ is unbounded, which is the desired contradiction.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Find all positive integers $k>1$ for which there exists a positive integer $n$ such that $\binom{n}{k}$ is divisible by $n$, and $\binom{n}{m}$ is not divisible by $n$ for $2 \leq m<k$.
|
Such an $n$ exists for any $k$. First, suppose $k$ is prime. We choose $n=(k-1)$ !. For $m<k$, it follows from $m!\mid n$ that $$ \begin{aligned} (n-1)(n-2) \cdots(n-m+1) & \equiv(-1)(-2) \cdots(-m+1) \\ & \equiv(-1)^{m-1}(m-1)! \\ & \not \equiv 0 \bmod m! \end{aligned} $$ We see that $\binom{n}{m}$ is not a multiple of $m$. For $m=k$, note that $\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$. Because $k \nmid n$, we must have $k \left\lvert\,\binom{ n-1}{k-1}\right.$, and it follows that $n \left\lvert\,\binom{ n}{k}\right.$. Now suppose $k$ is composite. We will choose $n$ to satisfy a number of congruence relations. For each prime $p \leq k$, let $$ t_{p}=\nu_{p}(\operatorname{lcm}(1,2, \ldots, k-1))=\max \left(\nu_{p}(1), \nu_{p}(2), \ldots, \nu_{p}(k-1)\right) $$ and choose $k_{p} \in\{1,2, \ldots, k-1\}$ as large as possible such that $\nu_{p}\left(k_{p}\right)=t_{p}$. We now require $$ \begin{aligned} n \equiv 0 \quad \bmod p^{t_{p}+1} & \text { if } p \nmid k \\ \nu_{p}\left(n-k_{p}\right)=t_{p}+\nu_{p}(k) & \text { if } p \mid k \end{aligned} $$ for all $p \leq k$. From the Chinese Remainder Theorem, we know that an $n$ exists that satisfies (1) and (2) (indeed, a sufficient condition for (2) is the congruence $n \equiv$ $\left.k_{p}+p^{t_{p}+\nu_{p}(k)} \bmod p^{t_{p}+\nu_{p}(k)+1}\right)$. We show that this $n$ has the required property. We first will compute $\nu_{p}(n-i)$ for primes $p<k$ and $1 \leq i<k$. - If $p \nmid k$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n)>t_{p}$, so $\nu_{p}(n-i)=\nu_{p}(i)$; - If $p \mid k$ and $i \neq k_{p}$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n) \geq t_{p}$, so again $\nu_{p}(n-i)=\nu_{p}(i) ;$ - If $p \mid k$ and $i=k_{p}$, then we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ by (2). We conclude that $\nu_{p}(n-i)=\nu_{p}(i)$ always holds, except when $i=k_{p}$, when we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ (this formula holds irrespective of whether $p \mid k$ or $\left.p \nmid k\right)$. We can now show that $\binom{n}{k}$ is divisible by $n$, which amounts to showing that $k$ ! divides $(n-1)(n-2) \cdots(n-k+1)$. Indeed, for each prime $p \leq k$ we have $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-k+1)) & =\nu_{p}\left(n-k_{p}\right)+\sum_{i<k, i \neq k_{p}} \nu_{p}(n-i) \\ & =\nu_{p}\left(k_{p}\right)+\nu_{p}(k)+\sum_{i<k, i \neq k_{p}} \nu_{p}(i) \end{aligned} $$ $$ =\sum_{i=1}^{k} \nu_{p}(i)=\nu_{p}(k!) $$ so it follows that $(n-1)(n-2) \cdots(n-k+1)$ is a multiple of $k$ !. Finally, let $1<m<k$. We will show that $n$ does not divide $\binom{n}{m}$, which amounts to showing that $m$ ! does not divide $(n-1)(n-2) \cdots(n-m+1)$. First, suppose that $m$ has a prime divisor $q$ that does not divide $k$. Then we have $$ \begin{aligned} \nu_{q}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{q}(n-i) \\ & =\sum_{i=1}^{m-1} \nu_{q}(i) \\ & =\nu_{q}((m-1)!)<\nu_{q}(m!) \end{aligned} $$ as desired. Therefore, suppose that $m$ is only divisible by primes that divide $k$. If there is such a prime $p$ with $\nu_{p}(m)>\nu_{p}(k)$, then it follows that $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\nu_{p}(k)+\sum_{i=1}^{m-1} \nu_{p}(i) \\ & <\nu_{p}(m)+\sum_{i=1}^{m-1} \nu_{p}(i) \\ & =\nu_{p}(m!) \end{aligned} $$ so $m$ ! cannot divide $(n-1)(n-2) \ldots(n-m+1)$. On the other hand, suppose that $\nu_{p}(m) \leq \nu_{p}(k)$ for all $p \mid k$, which would mean that $m \mid k$ and hence $m \leq \frac{k}{2}$. Consider a prime $p$ dividing $m$. We have $k_{p} \geq \frac{k}{2}$, because otherwise $2 k_{p}$ could have been used instead of $k_{p}$. It follows that $m \leq \frac{k}{2} \leq k_{p}$. Therefore, we obtain $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{p}(n-i) \\ & =\sum_{i=1}^{m-1} \nu_{p}(i) \\ & =\nu_{p}((m-1)!)<\nu_{p}(m!) \end{aligned} $$ showing that $(n-1)(n-2) \cdots(n-m+1)$ is not divisible by $m$ !. This shows that $\binom{n}{m}$ is not divisible by $n$ for $m<k$, and hence $n$ does have the required property.
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Find all positive integers $k>1$ for which there exists a positive integer $n$ such that $\binom{n}{k}$ is divisible by $n$, and $\binom{n}{m}$ is not divisible by $n$ for $2 \leq m<k$.
|
Such an $n$ exists for any $k$. First, suppose $k$ is prime. We choose $n=(k-1)$ !. For $m<k$, it follows from $m!\mid n$ that $$ \begin{aligned} (n-1)(n-2) \cdots(n-m+1) & \equiv(-1)(-2) \cdots(-m+1) \\ & \equiv(-1)^{m-1}(m-1)! \\ & \not \equiv 0 \bmod m! \end{aligned} $$ We see that $\binom{n}{m}$ is not a multiple of $m$. For $m=k$, note that $\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$. Because $k \nmid n$, we must have $k \left\lvert\,\binom{ n-1}{k-1}\right.$, and it follows that $n \left\lvert\,\binom{ n}{k}\right.$. Now suppose $k$ is composite. We will choose $n$ to satisfy a number of congruence relations. For each prime $p \leq k$, let $$ t_{p}=\nu_{p}(\operatorname{lcm}(1,2, \ldots, k-1))=\max \left(\nu_{p}(1), \nu_{p}(2), \ldots, \nu_{p}(k-1)\right) $$ and choose $k_{p} \in\{1,2, \ldots, k-1\}$ as large as possible such that $\nu_{p}\left(k_{p}\right)=t_{p}$. We now require $$ \begin{aligned} n \equiv 0 \quad \bmod p^{t_{p}+1} & \text { if } p \nmid k \\ \nu_{p}\left(n-k_{p}\right)=t_{p}+\nu_{p}(k) & \text { if } p \mid k \end{aligned} $$ for all $p \leq k$. From the Chinese Remainder Theorem, we know that an $n$ exists that satisfies (1) and (2) (indeed, a sufficient condition for (2) is the congruence $n \equiv$ $\left.k_{p}+p^{t_{p}+\nu_{p}(k)} \bmod p^{t_{p}+\nu_{p}(k)+1}\right)$. We show that this $n$ has the required property. We first will compute $\nu_{p}(n-i)$ for primes $p<k$ and $1 \leq i<k$. - If $p \nmid k$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n)>t_{p}$, so $\nu_{p}(n-i)=\nu_{p}(i)$; - If $p \mid k$ and $i \neq k_{p}$, then we have $\nu_{p}(i), \nu_{p}(n-i) \leq t_{p}$ and $\nu_{p}(n) \geq t_{p}$, so again $\nu_{p}(n-i)=\nu_{p}(i) ;$ - If $p \mid k$ and $i=k_{p}$, then we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ by (2). We conclude that $\nu_{p}(n-i)=\nu_{p}(i)$ always holds, except when $i=k_{p}$, when we have $\nu_{p}(n-i)=\nu_{p}(i)+\nu_{p}(k)$ (this formula holds irrespective of whether $p \mid k$ or $\left.p \nmid k\right)$. We can now show that $\binom{n}{k}$ is divisible by $n$, which amounts to showing that $k$ ! divides $(n-1)(n-2) \cdots(n-k+1)$. Indeed, for each prime $p \leq k$ we have $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-k+1)) & =\nu_{p}\left(n-k_{p}\right)+\sum_{i<k, i \neq k_{p}} \nu_{p}(n-i) \\ & =\nu_{p}\left(k_{p}\right)+\nu_{p}(k)+\sum_{i<k, i \neq k_{p}} \nu_{p}(i) \end{aligned} $$ $$ =\sum_{i=1}^{k} \nu_{p}(i)=\nu_{p}(k!) $$ so it follows that $(n-1)(n-2) \cdots(n-k+1)$ is a multiple of $k$ !. Finally, let $1<m<k$. We will show that $n$ does not divide $\binom{n}{m}$, which amounts to showing that $m$ ! does not divide $(n-1)(n-2) \cdots(n-m+1)$. First, suppose that $m$ has a prime divisor $q$ that does not divide $k$. Then we have $$ \begin{aligned} \nu_{q}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{q}(n-i) \\ & =\sum_{i=1}^{m-1} \nu_{q}(i) \\ & =\nu_{q}((m-1)!)<\nu_{q}(m!) \end{aligned} $$ as desired. Therefore, suppose that $m$ is only divisible by primes that divide $k$. If there is such a prime $p$ with $\nu_{p}(m)>\nu_{p}(k)$, then it follows that $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\nu_{p}(k)+\sum_{i=1}^{m-1} \nu_{p}(i) \\ & <\nu_{p}(m)+\sum_{i=1}^{m-1} \nu_{p}(i) \\ & =\nu_{p}(m!) \end{aligned} $$ so $m$ ! cannot divide $(n-1)(n-2) \ldots(n-m+1)$. On the other hand, suppose that $\nu_{p}(m) \leq \nu_{p}(k)$ for all $p \mid k$, which would mean that $m \mid k$ and hence $m \leq \frac{k}{2}$. Consider a prime $p$ dividing $m$. We have $k_{p} \geq \frac{k}{2}$, because otherwise $2 k_{p}$ could have been used instead of $k_{p}$. It follows that $m \leq \frac{k}{2} \leq k_{p}$. Therefore, we obtain $$ \begin{aligned} \nu_{p}((n-1)(n-2) \ldots(n-m+1)) & =\sum_{i=1}^{m-1} \nu_{p}(n-i) \\ & =\sum_{i=1}^{m-1} \nu_{p}(i) \\ & =\nu_{p}((m-1)!)<\nu_{p}(m!) \end{aligned} $$ showing that $(n-1)(n-2) \cdots(n-m+1)$ is not divisible by $m$ !. This shows that $\binom{n}{m}$ is not divisible by $n$ for $m<k$, and hence $n$ does have the required property.
|
{
"exam": "USA_TSTST",
"problem_label": "3",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system $$ \begin{aligned} m^{2}+a n+b & =(m+r)^{2} \\ n^{2}+a m+b & =(n+s)^{2} \end{aligned} $$ We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy. Claim - If $(r, s)$ is exceptional, then either - $0<r<a / 2$, and $0<s<\frac{1}{4} a^{2}$; or - $0<s<a / 2$, and $0<r<\frac{1}{4} a^{2}$; or - $r^{2}+s^{2} \leq 2 b$. In particular, finitely many pairs $(r, s)$ can be exceptional. $$ r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n $$ If $0<r<a / 2$, then the idea is to use the bound $a n+b \geq 2 m+1$ to get $m \leq \frac{a n+b-1}{2}$. Consequently, $$ (n+s)^{2}=n^{2}+a m+b \leq n^{2}+a \cdot \frac{a n+b-1}{2}+b $$ For this to hold for infinitely many integers $n$, we need $2 s \leq \frac{a^{2}}{2}$, by comparing coefficients. A similar case occurs when $0<s<a / 2$. If $\min (r, s)>a / 2$, then $(\dagger)$ forces $r^{2}+s^{2} \leq 2 b$, giving the last case. Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives $$ \begin{aligned} & a n=2 r m+r^{2}-b \\ & 2 s n=a m+b-s^{2} \end{aligned} $$ Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives $$ \frac{a}{2 s}=\frac{2 r}{a}=\frac{r^{2}-b}{b-s^{2}} $$ so $a=2 \sqrt{r s}$ and $b=\frac{s^{2} \sqrt{r}+r^{2} \sqrt{s}}{\sqrt{r}+\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\operatorname{gcd}(x, y)=1$. This gives $$ \begin{aligned} a & =2 k x y \\ b & =k^{2} x y\left(x^{2}-x y+y^{2}\right) \end{aligned} $$ Thus, $a \mid 2 b$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system $$ \begin{aligned} m^{2}+a n+b & =(m+r)^{2} \\ n^{2}+a m+b & =(n+s)^{2} \end{aligned} $$ We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy. Claim - If $(r, s)$ is exceptional, then either - $0<r<a / 2$, and $0<s<\frac{1}{4} a^{2}$; or - $0<s<a / 2$, and $0<r<\frac{1}{4} a^{2}$; or - $r^{2}+s^{2} \leq 2 b$. In particular, finitely many pairs $(r, s)$ can be exceptional. $$ r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n $$ If $0<r<a / 2$, then the idea is to use the bound $a n+b \geq 2 m+1$ to get $m \leq \frac{a n+b-1}{2}$. Consequently, $$ (n+s)^{2}=n^{2}+a m+b \leq n^{2}+a \cdot \frac{a n+b-1}{2}+b $$ For this to hold for infinitely many integers $n$, we need $2 s \leq \frac{a^{2}}{2}$, by comparing coefficients. A similar case occurs when $0<s<a / 2$. If $\min (r, s)>a / 2$, then $(\dagger)$ forces $r^{2}+s^{2} \leq 2 b$, giving the last case. Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives $$ \begin{aligned} & a n=2 r m+r^{2}-b \\ & 2 s n=a m+b-s^{2} \end{aligned} $$ Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives $$ \frac{a}{2 s}=\frac{2 r}{a}=\frac{r^{2}-b}{b-s^{2}} $$ so $a=2 \sqrt{r s}$ and $b=\frac{s^{2} \sqrt{r}+r^{2} \sqrt{s}}{\sqrt{r}+\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\operatorname{gcd}(x, y)=1$. This gives $$ \begin{aligned} a & =2 k x y \\ b & =k^{2} x y\left(x^{2}-x y+y^{2}\right) \end{aligned} $$ Thus, $a \mid 2 b$, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "4",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li). ## Lemma If $S$ is an independent set of $T$, then $$ \sum_{v \in S} \operatorname{deg}(v) \leq n-1 $$ Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$. We are given that there exists an independent set of at least $\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least $$ k+2 \cdot \frac{n-k-1}{2}=n-1 $$ Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li). ## Lemma If $S$ is an independent set of $T$, then $$ \sum_{v \in S} \operatorname{deg}(v) \leq n-1 $$ Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$. We are given that there exists an independent set of at least $\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least $$ k+2 \cdot \frac{n-k-1}{2}=n-1 $$ Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 2 (Andrew Gu). ## Lemma The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path. Now given a path of $a$ vertices, at most $\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is $$ \sum \frac{a_{i}+1}{2}=\frac{n+k-1}{2} . $$ For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 2 (Andrew Gu). ## Lemma The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path. Now given a path of $a$ vertices, at most $\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is $$ \sum \frac{a_{i}+1}{2}=\frac{n+k-1}{2} . $$ For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) Let the second tangent to $\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively. Let $h$ be inversion with respect to $\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$. Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\gamma$. Let $K$ be its center; its radius equals $\frac{1}{2} r$. Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $\gamma_{U}$ of center $K_{U}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\gamma_{V}$ of center $K_{V}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$. Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\overrightarrow{H H_{U}}$ and $\overrightarrow{D_{1} U}$ are equal. Consequently, $\overrightarrow{K K_{U}}=\frac{1}{2} \overrightarrow{D_{1} U}$. Similarly, $\overrightarrow{K K_{V}}=$ $\frac{1}{2} \overrightarrow{A_{1} V}$. Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\omega$, vectors $\overrightarrow{D_{1} U}$ and $\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\gamma_{U}$ and $\gamma_{V}$. As above, $h$ maps $\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\Omega_{A D}$. Since $E F$ and $P Q$ are parallel, triangles $\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\Omega_{A} \cup \omega_{A}$ and $\Omega_{A D} \cup \omega$. Consequently, we have $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right), $$ which solves part (a).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) Let the second tangent to $\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively. Let $h$ be inversion with respect to $\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$. Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\gamma$. Let $K$ be its center; its radius equals $\frac{1}{2} r$. Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $\gamma_{U}$ of center $K_{U}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\gamma_{V}$ of center $K_{V}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$. Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\overrightarrow{H H_{U}}$ and $\overrightarrow{D_{1} U}$ are equal. Consequently, $\overrightarrow{K K_{U}}=\frac{1}{2} \overrightarrow{D_{1} U}$. Similarly, $\overrightarrow{K K_{V}}=$ $\frac{1}{2} \overrightarrow{A_{1} V}$. Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\omega$, vectors $\overrightarrow{D_{1} U}$ and $\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\gamma_{U}$ and $\gamma_{V}$. As above, $h$ maps $\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\Omega_{A D}$. Since $E F$ and $P Q$ are parallel, triangles $\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\Omega_{A} \cup \omega_{A}$ and $\Omega_{A D} \cup \omega$. Consequently, we have $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right), $$ which solves part (a).
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\Omega$ again at $D^{\prime}$, so that $D^{\prime}$ is the Miquel point of $\{A B, A C, B C, P Q\}$. Since the quadrilateral formed by these lines has incircle $\omega$, it is classical that $D^{\prime} I$ bisects $\angle P D^{\prime} C$ and $B D^{\prime} Q$ (e.g. by DDIT). Let $\ell$ be the tangent to $\Omega$ at $D^{\prime}$ and $D^{\prime} I$ meet $\Omega$ again at $M$. We have $$ \measuredangle\left(\ell, D^{\prime} B\right)=\measuredangle D^{\prime} C B=\measuredangle D^{\prime} Q P=\measuredangle\left(D^{\prime} Q, E F\right) . $$ Therefore $D^{\prime} I$ also bisects the angle between $\ell$ and the line parallel to $E F$ through $D^{\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\prime}$ lies on $\operatorname{arc} B C$ not containing $A$, so $D^{\prime}=D$. Similarly, letting the second tangent to $\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic. ## Lemma There exists a circle $\Omega_{A D}$ tangent to $\Omega_{A}$ and $\Omega_{D}$ at $A$ and $D$, respectively. $$ \measuredangle O A O_{A}=\measuredangle(\perp E F, \perp B C)=\measuredangle(E F, B C) . $$ (Here, $\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\measuredangle O_{D} D O$. The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\Omega_{A}$ by homothety. Therefore it coincides with $\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\Omega$ again at $D^{\prime}$, so that $D^{\prime}$ is the Miquel point of $\{A B, A C, B C, P Q\}$. Since the quadrilateral formed by these lines has incircle $\omega$, it is classical that $D^{\prime} I$ bisects $\angle P D^{\prime} C$ and $B D^{\prime} Q$ (e.g. by DDIT). Let $\ell$ be the tangent to $\Omega$ at $D^{\prime}$ and $D^{\prime} I$ meet $\Omega$ again at $M$. We have $$ \measuredangle\left(\ell, D^{\prime} B\right)=\measuredangle D^{\prime} C B=\measuredangle D^{\prime} Q P=\measuredangle\left(D^{\prime} Q, E F\right) . $$ Therefore $D^{\prime} I$ also bisects the angle between $\ell$ and the line parallel to $E F$ through $D^{\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\prime}$ lies on $\operatorname{arc} B C$ not containing $A$, so $D^{\prime}=D$. Similarly, letting the second tangent to $\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic. ## Lemma There exists a circle $\Omega_{A D}$ tangent to $\Omega_{A}$ and $\Omega_{D}$ at $A$ and $D$, respectively. $$ \measuredangle O A O_{A}=\measuredangle(\perp E F, \perp B C)=\measuredangle(E F, B C) . $$ (Here, $\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\measuredangle O_{D} D O$. The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\Omega_{A}$ by homothety. Therefore it coincides with $\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) . $$
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Andrew Gu) Construct triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$. 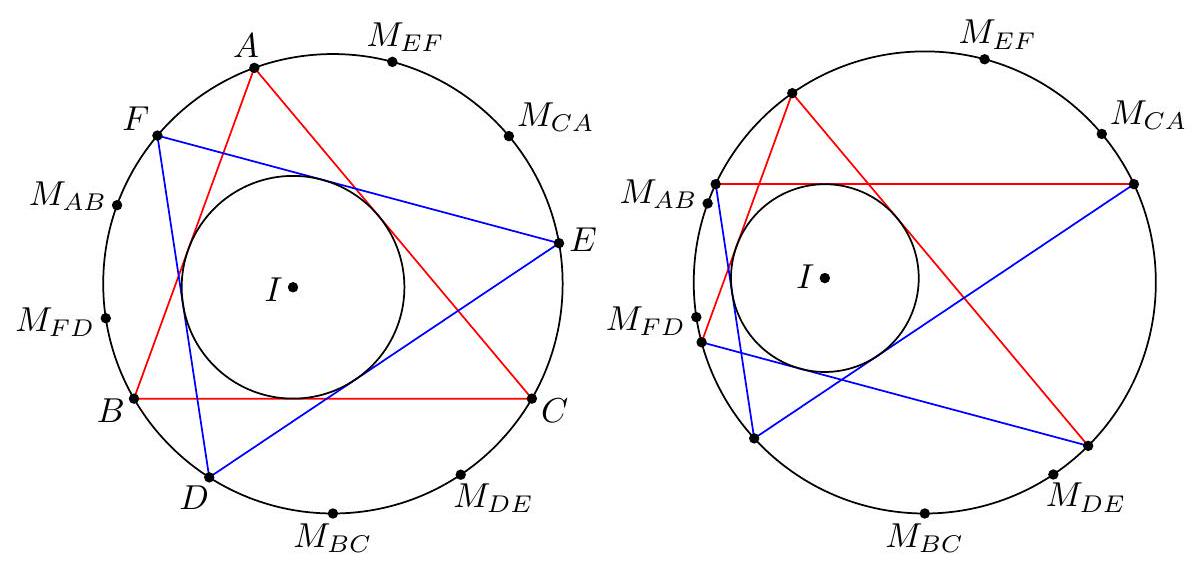 Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have $$ M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D} $$ Thus the copies of $\Delta_{A}$ and $\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Andrew Gu) Construct triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$.  Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have $$ M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D} $$ Thus the copies of $\Delta_{A}$ and $\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) By Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \cap I_{A} I_{D}$. Let $p$ be pole-and-polar correspondence with respect to $\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \cap E_{1} F_{1}$. Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line $I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$. Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\omega, A_{1} H \cdot H H_{A}$ equals half the power of $H$ with respect to $\omega$. Similarly, $D_{1} H \cdot H H_{D}$ equals half the power of $H$ with respect to $\omega$. Then $A_{1} H \cdot H H_{A}=D_{1} H \cdot H H_{D}$ and $A_{1} H H_{D} \sim D_{1} H H_{A}$. Since $\angle H H_{D} L_{A}=90^{\circ}=$ $\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently, $$ \frac{H L_{A}}{L_{A} A_{1}}=\frac{H L_{D}}{L_{D} D_{1}}=s $$ as a signed ratio. Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) By Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \cap I_{A} I_{D}$. Let $p$ be pole-and-polar correspondence with respect to $\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \cap E_{1} F_{1}$. Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line $I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$. Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\omega, A_{1} H \cdot H H_{A}$ equals half the power of $H$ with respect to $\omega$. Similarly, $D_{1} H \cdot H H_{D}$ equals half the power of $H$ with respect to $\omega$. Then $A_{1} H \cdot H H_{A}=D_{1} H \cdot H H_{D}$ and $A_{1} H H_{D} \sim D_{1} H H_{A}$. Since $\angle H H_{D} L_{A}=90^{\circ}=$ $\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently, $$ \frac{H L_{A}}{L_{A} A_{1}}=\frac{H L_{D}}{L_{D} D_{1}}=s $$ as a signed ratio. Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\omega$, let $\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter. Let $K_{A}$ and $K_{D}$ be the centers of $\gamma_{A}$ and $\gamma_{D}$, respectively, and let $\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\gamma_{A}$ and $\gamma_{D}$ are congruent (both of them are of radius $\left.\frac{1}{2} r\right)$, they are reflections of each other across $\ell_{A}$. Inversion $h$ maps the two common external tangents of $\Omega_{A}$ and $\Omega_{D}$ onto the two circles $\alpha$ and $\beta$ through $I$ that are tangent to both of $\gamma_{A}$ and $\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\alpha$ and $\beta$ are reflections of each other in $\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\ell_{A}$. Define $\ell_{B}, \ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\ell_{C}$. Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\omega$, let $\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter. Let $K_{A}$ and $K_{D}$ be the centers of $\gamma_{A}$ and $\gamma_{D}$, respectively, and let $\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\gamma_{A}$ and $\gamma_{D}$ are congruent (both of them are of radius $\left.\frac{1}{2} r\right)$, they are reflections of each other across $\ell_{A}$. Inversion $h$ maps the two common external tangents of $\Omega_{A}$ and $\Omega_{D}$ onto the two circles $\alpha$ and $\beta$ through $I$ that are tangent to both of $\gamma_{A}$ and $\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\alpha$ and $\beta$ are reflections of each other in $\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\ell_{A}$. Define $\ell_{B}, \ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\ell_{C}$. Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\Omega_{A}$ and $\Omega_{D}$. By Monge's theorem applied to $\Omega_{A}, \Omega_{D}$, and $\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear. The inversion at $T_{A}$ swapping $\Omega_{A}$ with $\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\Omega_{A}$ and $\Omega_{D}$ meet $\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \cap L_{A} L_{D}$. By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\Omega$. Therefore $A L_{A} \cap D L_{D}$ is the exsimilicenter $X$ of $\Omega$ and $\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\Omega_{A}$ and $\Omega_{D}$. By Monge's theorem applied to $\Omega_{A}, \Omega_{D}$, and $\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear. The inversion at $T_{A}$ swapping $\Omega_{A}$ with $\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\Omega_{A}$ and $\Omega_{D}$ meet $\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \cap L_{A} L_{D}$. By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\Omega$. Therefore $A L_{A} \cap D L_{D}$ is the exsimilicenter $X$ of $\Omega$ and $\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\Omega$.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\omega_{A}$ and $\omega_{D}$ respectively. By the Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\left(A, I_{A}, I\right),\left(D, I_{D}, I\right),\left(I_{A}, I_{D}, T\right)$. By Menelaus's theorem, we have $$ \frac{T_{A} D}{T_{A} A}=\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} . $$ If $s$ is the length of the side opposite $A$ in $\Delta_{A}$, then we compute $$ \begin{aligned} \frac{I_{A} I}{I_{A} A} & =\frac{s / \cos (A / 2)}{r_{A} / \sin (A / 2)} \\ & =\frac{2 R_{A} \sin (A) \sin (A / 2)}{\cos (A / 2)} \\ & =\frac{4 R_{A} \sin ^{2}(A / 2)}{r_{A}} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} . \end{aligned} $$ From part (a), we know that $\frac{R_{A}}{r_{A}}=\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\frac{I_{D} D}{I_{D} I}$, we get $$ \begin{aligned} \frac{T_{A} D}{T_{A} A} & =\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \cdot \frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\ & =\frac{D I^{2}}{A I^{2}} \end{aligned} $$ Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \cdot T_{A} D$. This shows what we claimed at the start.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\omega_{A}$ and $\omega_{D}$ respectively. By the Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\left(A, I_{A}, I\right),\left(D, I_{D}, I\right),\left(I_{A}, I_{D}, T\right)$. By Menelaus's theorem, we have $$ \frac{T_{A} D}{T_{A} A}=\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} . $$ If $s$ is the length of the side opposite $A$ in $\Delta_{A}$, then we compute $$ \begin{aligned} \frac{I_{A} I}{I_{A} A} & =\frac{s / \cos (A / 2)}{r_{A} / \sin (A / 2)} \\ & =\frac{2 R_{A} \sin (A) \sin (A / 2)}{\cos (A / 2)} \\ & =\frac{4 R_{A} \sin ^{2}(A / 2)}{r_{A}} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} . \end{aligned} $$ From part (a), we know that $\frac{R_{A}}{r_{A}}=\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\frac{I_{D} D}{I_{D} I}$, we get $$ \begin{aligned} \frac{T_{A} D}{T_{A} A} & =\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \cdot \frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\ & =\frac{D I^{2}}{A I^{2}} \end{aligned} $$ Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \cdot T_{A} D$. This shows what we claimed at the start.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 5 (Ankit Bisain) As in the previous solution, it suffices to show that $\frac{I_{A} I}{A I_{A}} \cdot \frac{D I_{D}}{I_{D} I}=\frac{D I^{2}}{A I^{2}}$. Let $A I$ and $D I$ meet $\Omega$ again at $M$ and $N$, respectively. Let $\ell$ be the line parallel to $B C$ and tangent to $\omega$ but different from $B C$. Then $$ \frac{D I_{D}}{I_{D} I}=\frac{d(D, B C)}{d(B C, \ell)}=\frac{D B \cdot D C / 2 R}{2 r}=\frac{M I^{2}-M D^{2}}{4 R r} $$ Since $I D M \sim I A N$, we have $$ \frac{D I_{D}}{I_{D} I} \cdot \frac{I_{A} I}{A I_{A}}=\frac{M I^{2}-M D^{2}}{N I^{2}-N A^{2}}=\frac{D I^{2}}{A I^{2}} $$ as desired. Remark (Author comments on generalization of part (b) with a circumscribed hexagram). Let triangles $A B C$ and $D E F$ be circumscribed about the same circle $\omega$ so that they form a hexagram. However, we do not require anymore that they are inscribed in the same circle. Define circles $\Omega_{A}, \omega_{A}, \ldots, \omega_{F}$ as in the problem. Let $T_{A}^{\text {Circ }}$ be the intersection point of the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$, and define points $T_{B}^{\text {Circ }}$ and $T_{C}^{\text {Circ }}$ similarly. Also let $T_{A}^{\text {In }}$ be the intersection point of the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$, and define points $T_{B}^{\mathrm{In}}$ and $T_{C}^{\mathrm{In}}$ similarly. Then points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\mathrm{Circ}}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. For the incircles part of the generalisation, we start out as in the first solution to part (b) of the problem, and eventually we reduce everything to the following: Let points $A_{1}, B_{1}, C_{1}, D_{1}, E_{1}$, and $F_{1}$ lie on circle $\omega$. Let lines $B_{1} C_{1}$ and $E_{1} F_{1}$ meet at point $X_{A}$, let the line through $A_{1}$ parallel to $B_{1} C_{1}$ and the line through $D_{1}$ parallel to $E_{1} F_{1}$ meet at point $Z_{A}$, and define points $X_{B}, Z_{B}, X_{C}$, and $Z_{C}$ similarly. Then lines $X_{A} Z_{A}$, $X_{B} Z_{B}$, and $X_{C} Z_{C}$ are concurrent. Take $\omega$ as the unit circle and assign complex numbers $u, v, w, x, y$, and $z$ to points $A_{1}$, $F_{1}, B_{1}, D_{1}, C_{1}$, and $E_{1}$, respectively, so that when we permute $u, v, w, x, y$, and $z$ cyclically the configuration remains unchanged. Then by standard complex bash formulas we obtain that each two out of our three lines meet at $\varphi / \psi$, where $$ \varphi=\sum_{\mathrm{Cyc}} u^{2} v w(w x-w y+x y)(y-z) $$ and $$ \psi=-u^{2} w^{2} y^{2}-v^{2} x^{2} z^{2}-4 u v w x y z+\sum_{\mathrm{Cyc}} u^{2}(v w x y-v w x z+v w y z-v x y z+w x y z) $$ (But the calculations were too difficult for me to do by hand, so I used SymPy.) Remark (Author comments on generalization of part (b) with an inscribed hexagram). Let triangles $A B C$ and $D E F$ be inscribed inside the same circle $\Omega$ so that they form a hexagram. However, we do not require anymore that they are circumscribed about the same circle. Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remark. It looks like once again points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. However, I do not have proofs of these claims. Remark (Further generalization from Andrew Gu). Let $A B C$ and $D E F$ be triangles which share an inconic, or equivalently share a circumconic. Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remarks. Then it is conjectured that points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. (Note that extraversion may be required depending on the configuration of points, e.g. excircles instead of incircles.) Additionally, it appears that the insimilicenters of the circumcircles lie on a line perpendicular to the line through $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 5 (Ankit Bisain) As in the previous solution, it suffices to show that $\frac{I_{A} I}{A I_{A}} \cdot \frac{D I_{D}}{I_{D} I}=\frac{D I^{2}}{A I^{2}}$. Let $A I$ and $D I$ meet $\Omega$ again at $M$ and $N$, respectively. Let $\ell$ be the line parallel to $B C$ and tangent to $\omega$ but different from $B C$. Then $$ \frac{D I_{D}}{I_{D} I}=\frac{d(D, B C)}{d(B C, \ell)}=\frac{D B \cdot D C / 2 R}{2 r}=\frac{M I^{2}-M D^{2}}{4 R r} $$ Since $I D M \sim I A N$, we have $$ \frac{D I_{D}}{I_{D} I} \cdot \frac{I_{A} I}{A I_{A}}=\frac{M I^{2}-M D^{2}}{N I^{2}-N A^{2}}=\frac{D I^{2}}{A I^{2}} $$ as desired. Remark (Author comments on generalization of part (b) with a circumscribed hexagram). Let triangles $A B C$ and $D E F$ be circumscribed about the same circle $\omega$ so that they form a hexagram. However, we do not require anymore that they are inscribed in the same circle. Define circles $\Omega_{A}, \omega_{A}, \ldots, \omega_{F}$ as in the problem. Let $T_{A}^{\text {Circ }}$ be the intersection point of the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$, and define points $T_{B}^{\text {Circ }}$ and $T_{C}^{\text {Circ }}$ similarly. Also let $T_{A}^{\text {In }}$ be the intersection point of the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$, and define points $T_{B}^{\mathrm{In}}$ and $T_{C}^{\mathrm{In}}$ similarly. Then points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\mathrm{Circ}}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. For the incircles part of the generalisation, we start out as in the first solution to part (b) of the problem, and eventually we reduce everything to the following: Let points $A_{1}, B_{1}, C_{1}, D_{1}, E_{1}$, and $F_{1}$ lie on circle $\omega$. Let lines $B_{1} C_{1}$ and $E_{1} F_{1}$ meet at point $X_{A}$, let the line through $A_{1}$ parallel to $B_{1} C_{1}$ and the line through $D_{1}$ parallel to $E_{1} F_{1}$ meet at point $Z_{A}$, and define points $X_{B}, Z_{B}, X_{C}$, and $Z_{C}$ similarly. Then lines $X_{A} Z_{A}$, $X_{B} Z_{B}$, and $X_{C} Z_{C}$ are concurrent. Take $\omega$ as the unit circle and assign complex numbers $u, v, w, x, y$, and $z$ to points $A_{1}$, $F_{1}, B_{1}, D_{1}, C_{1}$, and $E_{1}$, respectively, so that when we permute $u, v, w, x, y$, and $z$ cyclically the configuration remains unchanged. Then by standard complex bash formulas we obtain that each two out of our three lines meet at $\varphi / \psi$, where $$ \varphi=\sum_{\mathrm{Cyc}} u^{2} v w(w x-w y+x y)(y-z) $$ and $$ \psi=-u^{2} w^{2} y^{2}-v^{2} x^{2} z^{2}-4 u v w x y z+\sum_{\mathrm{Cyc}} u^{2}(v w x y-v w x z+v w y z-v x y z+w x y z) $$ (But the calculations were too difficult for me to do by hand, so I used SymPy.) Remark (Author comments on generalization of part (b) with an inscribed hexagram). Let triangles $A B C$ and $D E F$ be inscribed inside the same circle $\Omega$ so that they form a hexagram. However, we do not require anymore that they are circumscribed about the same circle. Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remark. It looks like once again points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. However, I do not have proofs of these claims. Remark (Further generalization from Andrew Gu). Let $A B C$ and $D E F$ be triangles which share an inconic, or equivalently share a circumconic. Define points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}, \ldots, T_{C}^{\mathrm{In}}$ as in the previous remarks. Then it is conjectured that points $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$ are collinear and points $T_{A}^{\mathrm{In}}, T_{B}^{\mathrm{In}}$, and $T_{C}^{\mathrm{In}}$ are also collinear. (Note that extraversion may be required depending on the configuration of points, e.g. excircles instead of incircles.) Additionally, it appears that the insimilicenters of the circumcircles lie on a line perpendicular to the line through $T_{A}^{\text {Circ }}, T_{B}^{\text {Circ }}$, and $T_{C}^{\text {Circ }}$.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
【 Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases: Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$. By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$. Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path. Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \leq k \leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths. This completes the induction step, which solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
【 Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases: Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$. By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$. Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path. Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \leq k \leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths. This completes the induction step, which solves the problem.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
## 【 Solution 2. ## Lemma If $|M|<n$, there is more than one mine-avoiding path. - Make the first $i+1$ points $P_{0}, P_{1}, \ldots, P_{i}$. - If $P_{i} \rightarrow P_{i+1}$ is one unit up, go right until $\left(n-y_{i}, y_{i}\right)$. - If $P_{i} \rightarrow P_{i+1}$ is one unit right, go up until $\left(x_{i}, n-x_{i}\right)$.  The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue. By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding. Now, consider the following process: - Start at $(0,0)$. - If there is only one choice of next step that is part of a mine-avoiding path, make that choice. - Repeat the above until at a point with two possible steps that are part of mineavoiding paths. - Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.  For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$. This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.
|
2^{n-|M|}
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
## 【 Solution 2. ## Lemma If $|M|<n$, there is more than one mine-avoiding path. - Make the first $i+1$ points $P_{0}, P_{1}, \ldots, P_{i}$. - If $P_{i} \rightarrow P_{i+1}$ is one unit up, go right until $\left(n-y_{i}, y_{i}\right)$. - If $P_{i} \rightarrow P_{i+1}$ is one unit right, go up until $\left(x_{i}, n-x_{i}\right)$.  The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue. By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding. Now, consider the following process: - Start at $(0,0)$. - If there is only one choice of next step that is part of a mine-avoiding path, make that choice. - Repeat the above until at a point with two possible steps that are part of mineavoiding paths. - Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.  For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$. This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
ब Solution 1 (author). We'll use the following lemma. ## Lemma Suppose that $P Q R S$ is a convex quadrilateral with $\angle P=\angle R$. Then there is a point $T$ on $Q S$ such that $\angle Q P T=\angle S R P, \angle T R Q=\angle R P S$, and $P T=R T$. Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\angle A=\angle A_{1}$ shows that $\angle B_{1} A_{1} A_{2}=\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\triangle A B C$. Then $\triangle A_{2} B_{2} C_{2} \sim \triangle A_{1} B_{1} C_{1} \sim \triangle A B C$, as desired. Additionally, $P T=R T$ is a corollary of the angle conditions because $$ \measuredangle P R T=\measuredangle S R Q-\measuredangle T R Q-\measuredangle S R P=\measuredangle Q P S-\measuredangle R P S-\measuredangle Q P T=\measuredangle T P R $$ Therefore we only need to prove the angle conditions.  $$ \begin{aligned} \measuredangle P X T & =\measuredangle R^{\prime} P Q+\measuredangle P Q S \\ & =\measuredangle R^{\prime} S Q+\measuredangle P Q S \\ & =\measuredangle Q S R+\measuredangle P Q S \\ & =\measuredangle(P Q, S R) \\ & =\measuredangle Q P R+\measuredangle P R S . \end{aligned} $$ This means that $$ \begin{aligned} \measuredangle Q P T & =\measuredangle Q P R-\measuredangle T P R \\ & =\measuredangle Q P R-\measuredangle T X R \\ & =\measuredangle Q P R-\measuredangle P X T \\ & =\measuredangle Q P R-\measuredangle Q P R-\measuredangle P R S \\ & =\measuredangle S R P . \end{aligned} $$ Similarly, $\measuredangle Q R T=\measuredangle S P R$, so we're done.  $$ \frac{Q T}{T S}=\frac{\sin Q P T \cdot P T / \sin P Q T}{\sin T P S \cdot P T / \sin T S P}=\frac{P Q / \sin P R Q}{P S / \sin S R P}=\frac{R(\triangle P Q R)}{R(\triangle P R S)} $$ which is symmetric in $P$ and $R$, so we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
ब Solution 1 (author). We'll use the following lemma. ## Lemma Suppose that $P Q R S$ is a convex quadrilateral with $\angle P=\angle R$. Then there is a point $T$ on $Q S$ such that $\angle Q P T=\angle S R P, \angle T R Q=\angle R P S$, and $P T=R T$. Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\angle A=\angle A_{1}$ shows that $\angle B_{1} A_{1} A_{2}=\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\triangle A B C$. Then $\triangle A_{2} B_{2} C_{2} \sim \triangle A_{1} B_{1} C_{1} \sim \triangle A B C$, as desired. Additionally, $P T=R T$ is a corollary of the angle conditions because $$ \measuredangle P R T=\measuredangle S R Q-\measuredangle T R Q-\measuredangle S R P=\measuredangle Q P S-\measuredangle R P S-\measuredangle Q P T=\measuredangle T P R $$ Therefore we only need to prove the angle conditions.  $$ \begin{aligned} \measuredangle P X T & =\measuredangle R^{\prime} P Q+\measuredangle P Q S \\ & =\measuredangle R^{\prime} S Q+\measuredangle P Q S \\ & =\measuredangle Q S R+\measuredangle P Q S \\ & =\measuredangle(P Q, S R) \\ & =\measuredangle Q P R+\measuredangle P R S . \end{aligned} $$ This means that $$ \begin{aligned} \measuredangle Q P T & =\measuredangle Q P R-\measuredangle T P R \\ & =\measuredangle Q P R-\measuredangle T X R \\ & =\measuredangle Q P R-\measuredangle P X T \\ & =\measuredangle Q P R-\measuredangle Q P R-\measuredangle P R S \\ & =\measuredangle S R P . \end{aligned} $$ Similarly, $\measuredangle Q R T=\measuredangle S P R$, so we're done.  $$ \frac{Q T}{T S}=\frac{\sin Q P T \cdot P T / \sin P Q T}{\sin T P S \cdot P T / \sin T S P}=\frac{P Q / \sin P R Q}{P S / \sin S R P}=\frac{R(\triangle P Q R)}{R(\triangle P R S)} $$ which is symmetric in $P$ and $R$, so we're done.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
Solution 2 (Ankan Bhattacharya). We prove the main claim $\frac{B_{1} A_{2}}{A_{2} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Let $\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\triangle A B C$. In addition, let $A_{1}^{\prime}$ be the reflection of $A_{1}$ over $\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\triangle X B C \approx \triangle A B_{1} C_{1}$, so that we have a compound similarity $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Finally, let $O_{A}$ be the circumcenter of $\triangle A_{1}^{\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\overline{B_{1} C_{1}}$ satisfying $\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Recall that $O$ is the Miquel point of $\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter. Claim $-\overline{A A_{1}^{\prime}} \| \overline{B C}$. $$ \text { Claim }-\overline{A X} \| \overline{B_{1} C_{1}} . $$ $$ \measuredangle(\overline{B C}, \overline{A X})=\measuredangle\left(\overline{A A_{1}^{\prime}}, \overline{B_{1} C_{1}}\right) . $$ As $\overline{A A_{1}^{\prime}} \| \overline{B C}$, we obtain $\overline{A X} \| \overline{B_{1} C_{1}}$. $$ \text { Claim }-\overline{A X} \perp \overline{A_{1} O} . $$ $$ \text { Claim }-\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}} $$ $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Claim $-A A_{2}^{*}=A_{1}^{\prime} A_{2}$. Finally, $A_{1}^{\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
Solution 2 (Ankan Bhattacharya). We prove the main claim $\frac{B_{1} A_{2}}{A_{2} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Let $\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\triangle A B C$. In addition, let $A_{1}^{\prime}$ be the reflection of $A_{1}$ over $\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\triangle X B C \approx \triangle A B_{1} C_{1}$, so that we have a compound similarity $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Finally, let $O_{A}$ be the circumcenter of $\triangle A_{1}^{\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\overline{B_{1} C_{1}}$ satisfying $\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Recall that $O$ is the Miquel point of $\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter. Claim $-\overline{A A_{1}^{\prime}} \| \overline{B C}$. $$ \text { Claim }-\overline{A X} \| \overline{B_{1} C_{1}} . $$ $$ \measuredangle(\overline{B C}, \overline{A X})=\measuredangle\left(\overline{A A_{1}^{\prime}}, \overline{B_{1} C_{1}}\right) . $$ As $\overline{A A_{1}^{\prime}} \| \overline{B C}$, we obtain $\overline{A X} \| \overline{B_{1} C_{1}}$. $$ \text { Claim }-\overline{A X} \perp \overline{A_{1} O} . $$ $$ \text { Claim }-\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}} $$ $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Claim $-A A_{2}^{*}=A_{1}^{\prime} A_{2}$. Finally, $A_{1}^{\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that $$ \sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}} $$ is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). 【 Solution 1 (author). Let $\zeta_{p}=e^{2 \pi i / p}$ be a fixed primitive $p$ th root of unity. Observe that the given sum is an integer for all $n \leq 0$ (e.g. because the sum is an integer symmetric polynomial in the primitive $q$ th roots of unity). By expanding polynomials in the basis $(1-x)^{k}$, it follows that if the sum in the problem statement is an integer for all $n<n_{0}$, then $$ \sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{n}} \in \mathbb{Z} $$ for all $n<n_{0}$ and $f \in \mathbb{Z}[x]$, whereas for $n=n_{0}$ there is some $f \in \mathbb{Z}[x]$ for which the sum is not an integer (e.g. $f=1$ ). Let $z_{q}=r \phi(q)-q / p=p^{r-1}[r(p-1)-1]$. We claim that the answer is $n=z_{q}+1$. We prove this by induction on $r$. First is the base case $r=1$. ## Lemma There exist polynomials $u, v \in \mathbb{Z}[x]$ such that $(1-\omega)^{p-1} / p=u(\omega)$ and $p /(1-\omega)^{p-1}=$ $v(\omega)$ for all $\omega \in S_{p}$. (What we are saying is that $p$ is $(1-\omega)^{p-1}$ times a unit (invertible algebraic integer), namely $v(\omega)$.) $$ \frac{p}{(1-\omega)^{p-1}}=\frac{1-\omega}{1-\omega} \cdot \frac{1-\omega^{2}}{1-\omega} \cdots \frac{1-\omega^{p-1}}{1-\omega} $$ and take $$ v(x)=\prod_{k=1}^{p-1} \frac{1-x^{k}}{1-x} $$ Similarly, the polynomial $u$ is $$ u(x)=\prod_{k=1}^{p-1} \frac{1-x^{k \ell_{k}}}{1-x^{k}} $$ where $\ell_{k}$ is a multiplicative inverse of $k$ modulo $p$. Now, the main idea: given $g \in \mathbb{Z}[x]$, observe that $$ S=\sum_{\omega \in S_{p}}(1-\omega) g(\omega) $$ is divisible by $1-\zeta_{p}^{k}$ (i.e. it is $1-\zeta_{p}^{k}$ times an algebraic integer) for every $k$ coprime to $p$. By symmetric sums, $S$ is an integer; since $S^{p-1}$ is divisible by $\left(1-\zeta_{p}\right) \cdots\left(1-\zeta_{p}^{p-1}\right)=p$, the integer $S$ must itself be divisible by $p$. (Alternatively, since $h(x):=(1-x) g(x)$ vanishes at $x=1$, one can interpret $S$ using a roots of unity filter: $S=p \cdot h\left(\left[x^{0}\right]+\left[x^{p}\right]+\cdots\right) \equiv 0$ $(\bmod p)$.$) Now write$ $$ \mathbb{Z} \ni \frac{S}{p}=\sum_{\omega \in S_{p}} \frac{(1-\omega)^{p-1}}{p} \frac{g(\omega)}{(1-\omega)^{p-2}}=\sum_{\omega \in S_{p}} u(\omega) \frac{g(\omega)}{(1-\omega)^{p-2}} . $$ Taking $g=v \cdot(1-x)^{k}$ for $k \geq 0$, we see that the sum in the problem statement is an integer for any $n \leq p-2$. Finally, we have $$ \sum_{\omega \in S_{p}} \frac{u(\omega)}{(1-\omega)^{p-1}}=\sum_{\omega \in S_{p}} \frac{1}{p}=\frac{p-1}{p} \notin \mathbb{Z} $$ so the sum is not an integer for $n=p-1$. Now let $r \geq 2$ and assume the induction hypothesis for $r-1$. ## Lemma There exist polynomials $U, V \in \mathbb{Z}[x]$ such that $(1-\omega)^{p} /\left(1-\omega^{p}\right)=U(\omega)$ and $\left(1-\omega^{p}\right) /(1-\omega)^{p}=V(\omega)$ for all $\omega \in S_{q}$. (Again, these are units.) $$ \begin{aligned} U(x) & =\prod_{k=1}^{p-1} \frac{1-x^{(k q / p+1) \ell_{k}}}{1-x^{k q / p+1}} \\ V(x) & =\prod_{k=1}^{p-1} \frac{1-x^{k q / p+1}}{1-x} \end{aligned} $$ where $\ell_{k}$ is a multiplicative inverse of $k q / p+1$ modulo $q$. ## Corollary If $\omega \in S_{q}$, then $(1-\omega)^{\phi(q)} / p$ is a unit. Thus we have polynomials $A, B \in \mathbb{Z}[x]$ such that $$ \begin{aligned} & A(\omega)=\frac{p}{(1-\omega)^{\phi(q)}} V(\omega)^{z_{q / p}} \\ & B(\omega)=\frac{(1-\omega)^{\phi(q)}}{p} U(\omega)^{z_{q / p}} \end{aligned} $$ for all $\omega \in S_{q}$. Given $g \in \mathbb{Z}[x]$, consider the $p$ th roots of unity filter $$ S(x):=\sum_{k=0}^{p-1} g\left(\zeta_{p}^{k} x\right)=p \cdot h\left(x^{p}\right) $$ where $h \in \mathbb{Z}[x]$. Then $$ p h(\eta)=S(\omega)=\sum_{\omega^{p}=\eta} g(\omega) $$ for all $\eta \in S_{q / p}$, so $$ \begin{aligned} \frac{h(\eta)}{(1-\eta)^{z_{q / p}}}=\frac{S(\omega)}{p(1-\eta)^{z_{q / p}}} & =\sum_{\omega^{p}=\eta} \frac{(1-\omega)^{p z_{q / p}}}{\left(1-\omega^{p}\right)^{z_{q / p}}} \frac{g(\omega)}{p(1-\omega)^{p z_{q / p}}} \\ & =\sum_{\omega^{p}=\eta} U(\omega)^{z_{q / p}} \frac{(1-\omega)^{\phi(q)}}{p} \frac{g(\omega)}{(1-\omega)^{z_{q}}} \end{aligned} $$ (Implicit in the last line is $z_{q}=\phi(q)+p z_{q / p}$.) Since $U(\omega)$ and $(1-\omega)^{\phi(q)} / p$ are units, we can let $g=A \cdot f$ for arbitrary $f \in \mathbb{Z}[x]$, so that the expression in the summation simplifies to $f(\omega) /(1-\omega)^{z_{q}}$. From this we conclude that for any $f \in \mathbb{Z}[x]$, there exists $h \in \mathbb{Z}[x]$ such that $$ \begin{aligned} \sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{z_{q}}} & =\sum_{\eta \in S_{q / p}} \sum_{\omega^{p}=\eta} \frac{f(\omega)}{(1-\omega)^{z_{q}}} \\ & =\sum_{\eta \in S_{q / p}} \frac{h(\eta)}{(1-\eta)^{z_{q / p}}} \end{aligned} $$ By the inductive hypothesis, this is always an integer. In the other direction, for $\eta \in S_{q / p}$ we have $$ \begin{aligned} \sum_{\omega^{p}=\eta} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}} & =\sum_{\omega^{p}=\eta} \frac{1}{p\left(1-\omega^{p}\right)^{z_{q / p}}(1-\omega)} \\ & =\frac{1}{p(1-\eta)^{z_{q / p}}} \sum_{\omega^{p}=\eta} \frac{1}{1-\omega} \\ & =\frac{1}{p(1-\eta)^{z_{q / p}}}\left[\frac{p x^{p-1}}{x^{p}-\eta}\right]_{x=1} \\ & =\frac{1}{(1-\eta)^{1+z_{q / p}}} \end{aligned} $$ Summing over all $\eta \in S_{q / p}$, we conclude by the inductive hypothesis that $$ \sum_{\omega \in S_{q}} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}}=\sum_{\eta \in S_{q / p}} \frac{1}{(1-\eta)^{1+z_{q / p}}} $$
|
z_{q}+1
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that $$ \sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}} $$ is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). 【 Solution 1 (author). Let $\zeta_{p}=e^{2 \pi i / p}$ be a fixed primitive $p$ th root of unity. Observe that the given sum is an integer for all $n \leq 0$ (e.g. because the sum is an integer symmetric polynomial in the primitive $q$ th roots of unity). By expanding polynomials in the basis $(1-x)^{k}$, it follows that if the sum in the problem statement is an integer for all $n<n_{0}$, then $$ \sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{n}} \in \mathbb{Z} $$ for all $n<n_{0}$ and $f \in \mathbb{Z}[x]$, whereas for $n=n_{0}$ there is some $f \in \mathbb{Z}[x]$ for which the sum is not an integer (e.g. $f=1$ ). Let $z_{q}=r \phi(q)-q / p=p^{r-1}[r(p-1)-1]$. We claim that the answer is $n=z_{q}+1$. We prove this by induction on $r$. First is the base case $r=1$. ## Lemma There exist polynomials $u, v \in \mathbb{Z}[x]$ such that $(1-\omega)^{p-1} / p=u(\omega)$ and $p /(1-\omega)^{p-1}=$ $v(\omega)$ for all $\omega \in S_{p}$. (What we are saying is that $p$ is $(1-\omega)^{p-1}$ times a unit (invertible algebraic integer), namely $v(\omega)$.) $$ \frac{p}{(1-\omega)^{p-1}}=\frac{1-\omega}{1-\omega} \cdot \frac{1-\omega^{2}}{1-\omega} \cdots \frac{1-\omega^{p-1}}{1-\omega} $$ and take $$ v(x)=\prod_{k=1}^{p-1} \frac{1-x^{k}}{1-x} $$ Similarly, the polynomial $u$ is $$ u(x)=\prod_{k=1}^{p-1} \frac{1-x^{k \ell_{k}}}{1-x^{k}} $$ where $\ell_{k}$ is a multiplicative inverse of $k$ modulo $p$. Now, the main idea: given $g \in \mathbb{Z}[x]$, observe that $$ S=\sum_{\omega \in S_{p}}(1-\omega) g(\omega) $$ is divisible by $1-\zeta_{p}^{k}$ (i.e. it is $1-\zeta_{p}^{k}$ times an algebraic integer) for every $k$ coprime to $p$. By symmetric sums, $S$ is an integer; since $S^{p-1}$ is divisible by $\left(1-\zeta_{p}\right) \cdots\left(1-\zeta_{p}^{p-1}\right)=p$, the integer $S$ must itself be divisible by $p$. (Alternatively, since $h(x):=(1-x) g(x)$ vanishes at $x=1$, one can interpret $S$ using a roots of unity filter: $S=p \cdot h\left(\left[x^{0}\right]+\left[x^{p}\right]+\cdots\right) \equiv 0$ $(\bmod p)$.$) Now write$ $$ \mathbb{Z} \ni \frac{S}{p}=\sum_{\omega \in S_{p}} \frac{(1-\omega)^{p-1}}{p} \frac{g(\omega)}{(1-\omega)^{p-2}}=\sum_{\omega \in S_{p}} u(\omega) \frac{g(\omega)}{(1-\omega)^{p-2}} . $$ Taking $g=v \cdot(1-x)^{k}$ for $k \geq 0$, we see that the sum in the problem statement is an integer for any $n \leq p-2$. Finally, we have $$ \sum_{\omega \in S_{p}} \frac{u(\omega)}{(1-\omega)^{p-1}}=\sum_{\omega \in S_{p}} \frac{1}{p}=\frac{p-1}{p} \notin \mathbb{Z} $$ so the sum is not an integer for $n=p-1$. Now let $r \geq 2$ and assume the induction hypothesis for $r-1$. ## Lemma There exist polynomials $U, V \in \mathbb{Z}[x]$ such that $(1-\omega)^{p} /\left(1-\omega^{p}\right)=U(\omega)$ and $\left(1-\omega^{p}\right) /(1-\omega)^{p}=V(\omega)$ for all $\omega \in S_{q}$. (Again, these are units.) $$ \begin{aligned} U(x) & =\prod_{k=1}^{p-1} \frac{1-x^{(k q / p+1) \ell_{k}}}{1-x^{k q / p+1}} \\ V(x) & =\prod_{k=1}^{p-1} \frac{1-x^{k q / p+1}}{1-x} \end{aligned} $$ where $\ell_{k}$ is a multiplicative inverse of $k q / p+1$ modulo $q$. ## Corollary If $\omega \in S_{q}$, then $(1-\omega)^{\phi(q)} / p$ is a unit. Thus we have polynomials $A, B \in \mathbb{Z}[x]$ such that $$ \begin{aligned} & A(\omega)=\frac{p}{(1-\omega)^{\phi(q)}} V(\omega)^{z_{q / p}} \\ & B(\omega)=\frac{(1-\omega)^{\phi(q)}}{p} U(\omega)^{z_{q / p}} \end{aligned} $$ for all $\omega \in S_{q}$. Given $g \in \mathbb{Z}[x]$, consider the $p$ th roots of unity filter $$ S(x):=\sum_{k=0}^{p-1} g\left(\zeta_{p}^{k} x\right)=p \cdot h\left(x^{p}\right) $$ where $h \in \mathbb{Z}[x]$. Then $$ p h(\eta)=S(\omega)=\sum_{\omega^{p}=\eta} g(\omega) $$ for all $\eta \in S_{q / p}$, so $$ \begin{aligned} \frac{h(\eta)}{(1-\eta)^{z_{q / p}}}=\frac{S(\omega)}{p(1-\eta)^{z_{q / p}}} & =\sum_{\omega^{p}=\eta} \frac{(1-\omega)^{p z_{q / p}}}{\left(1-\omega^{p}\right)^{z_{q / p}}} \frac{g(\omega)}{p(1-\omega)^{p z_{q / p}}} \\ & =\sum_{\omega^{p}=\eta} U(\omega)^{z_{q / p}} \frac{(1-\omega)^{\phi(q)}}{p} \frac{g(\omega)}{(1-\omega)^{z_{q}}} \end{aligned} $$ (Implicit in the last line is $z_{q}=\phi(q)+p z_{q / p}$.) Since $U(\omega)$ and $(1-\omega)^{\phi(q)} / p$ are units, we can let $g=A \cdot f$ for arbitrary $f \in \mathbb{Z}[x]$, so that the expression in the summation simplifies to $f(\omega) /(1-\omega)^{z_{q}}$. From this we conclude that for any $f \in \mathbb{Z}[x]$, there exists $h \in \mathbb{Z}[x]$ such that $$ \begin{aligned} \sum_{\omega \in S_{q}} \frac{f(\omega)}{(1-\omega)^{z_{q}}} & =\sum_{\eta \in S_{q / p}} \sum_{\omega^{p}=\eta} \frac{f(\omega)}{(1-\omega)^{z_{q}}} \\ & =\sum_{\eta \in S_{q / p}} \frac{h(\eta)}{(1-\eta)^{z_{q / p}}} \end{aligned} $$ By the inductive hypothesis, this is always an integer. In the other direction, for $\eta \in S_{q / p}$ we have $$ \begin{aligned} \sum_{\omega^{p}=\eta} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}} & =\sum_{\omega^{p}=\eta} \frac{1}{p\left(1-\omega^{p}\right)^{z_{q / p}}(1-\omega)} \\ & =\frac{1}{p(1-\eta)^{z_{q / p}}} \sum_{\omega^{p}=\eta} \frac{1}{1-\omega} \\ & =\frac{1}{p(1-\eta)^{z_{q / p}}}\left[\frac{p x^{p-1}}{x^{p}-\eta}\right]_{x=1} \\ & =\frac{1}{(1-\eta)^{1+z_{q / p}}} \end{aligned} $$ Summing over all $\eta \in S_{q / p}$, we conclude by the inductive hypothesis that $$ \sum_{\omega \in S_{q}} \frac{B(\omega)}{(1-\omega)^{1+z_{q}}}=\sum_{\eta \in S_{q / p}} \frac{1}{(1-\eta)^{1+z_{q / p}}} $$
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that $$ \sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}} $$ is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). Solution 2 (Nikolai Beluhov). Suppose that the complex numbers $\frac{1}{1-\omega}$ for $\omega \in S_{q}$ are the roots of $$ P(x)=x^{d}-c_{1} x^{d-1}+c_{2} x^{d-2}-\cdots \pm c_{d} $$ so that $c_{k}$ is their $k$-th elementary symmetric polynomial and $d=\phi(q)=(p-1) p^{r-1}$. Additionally denote $$ S_{n}=\sum_{\omega \in S_{q}} \frac{1}{(1-\omega)^{n}} $$ Then, by Newton's identities, $$ \begin{aligned} S_{1} & =c_{1} \\ S_{2} & =c_{1} S_{1}-2 c_{2} \\ S_{3} & =c_{1} S_{2}-c_{2} S_{1}+3 c_{3} \end{aligned} $$ and so on. The general pattern when $n \leq d$ is $$ S_{n}=\left[\sum_{j=1}^{n-1}(-1)^{j+1} c_{j} S_{n-j}\right]+(-1)^{n+1} n c_{n} $$ After that, when $n>d$, the pattern changes to $$ S_{n}=\sum_{j=1}^{d}(-1)^{j+1} c_{j} S_{n-j} $$ ## Lemma All of the $c_{i}$ are integers except for $c_{d}$. Furthermore, $c_{d}$ is $1 / p$ times an integer. $$ \Phi_{q}(x)=1+x^{p^{r-1}}+x^{2 p^{r-1}}+\cdots+x^{(p-1) p^{r-1}} $$ The polynomial $$ Q(x)=1+(1+x)^{p^{r-1}}+(1+x)^{2 p^{r-1}}+\cdots+(1+x)^{(p-1) p^{r-1}} $$ has roots $\omega-1$ for $\omega \in S_{q}$, so it is equal to $p(-x)^{d} P(-1 / x)$ by comparing constant coefficients. Comparing the remaining coefficients, we find that $c_{n}$ is $1 / p$ times the $x^{n}$ coefficient of $Q$. Since $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$, we conclude that, modulo $p$, $$ \begin{aligned} Q(x) & \equiv 1+\left(1+x^{p^{r-1}}\right)+\left(1+x^{p^{r-1}}\right)^{2}+\cdots+\left(1+x^{p^{r-1}}\right)^{p-1} \\ & \equiv\left[\left(1+x^{p^{r-1}}\right)^{p}-1\right] / x^{p^{r-1}} \end{aligned} $$ Since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, it follows that all coefficients of $Q(x)$ are multiples of $p$ save for the leading one. Therefore, $c_{n}$ is an integer when $n<d$, while $c_{d}$ is $1 / p$ times an integer. By the recurrences above, $S_{n}$ is an integer for $n<d$. When $r=1$, we get that $d c_{d}$ is not an integer, so $S_{d}$ is not an integer, either. Thus the answer for $r=1$ is $n=p-1$. Suppose now that $r \geq 2$. Then $d c_{d}$ does become an integer, so $S_{d}$ is an integer as well. ## Lemma For all $n$ with $1 \leq n \leq d$, we have $\nu_{p}\left(n c_{n}\right) \geq r-2$. Furthermore, the smallest $n$ such that $\nu_{p}\left(n c_{n}\right)=r-2$ is $d-p^{r-1}+1$. $$ p^{r-1}(1+x)^{p^{r-1}-1}\left[\sum_{k=1}^{p-1} k(1+x)^{(k-1) p^{r-1}}\right] . $$ What we want to prove reduces to showing that all coefficients of the polynomial in the square brackets are multiples of $p$ except for the leading one. Using the same trick $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$ as before and also writing $w$ for $x^{p^{r-1}}$, modulo $p$ the polynomial in the square brackets becomes $$ 1+2(1+w)+3(1+w)^{2}+\cdots+(p-1)(1+w)^{p-2} $$ This is the derivative of $$ 1+(1+w)+(1+w)^{2}+\cdots+(1+w)^{p-1}=\left[(1+w)^{p}-1\right] / w $$ and so, since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, we are done. Finally, we finish the problem with the following claim. Claim - Let $m=d-p^{r-1}$. Then for all $k \geq 0$ and $1 \leq j \leq d$, we have $$ \begin{aligned} & \nu_{p}\left(S_{k d+m+1}\right)=r-2-k \\ & \nu_{p}\left(S_{k d+m+j}\right) \geq r-2-k \end{aligned} $$ $$ \nu_{p}\left((m+1) c_{m+1}\right)=r-2 $$ and all other terms in the recurrence relation are divisible by $p^{r-1}$. We can similarly check that $\nu_{p}\left(S_{n}\right) \geq r-2$ for $m+1 \leq n \leq d$. Newton's identities combined with the first lemma now imply the following for $n>d$ : - If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right) \geq \ell+1$, then $\nu_{p}\left(S_{n}\right) \geq \ell$. - If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right)=\ell$, then $\nu_{p}\left(S_{n}\right)=\ell-1$. Together, these prove the claim by induction. By the claim, the smallest $n$ for which $\nu_{p}\left(S_{n}\right)<0$ (equivalent to $S_{n}$ not being an integer, by the recurrences) is $$ n=(r-1) d+m+1=((p-1) r-1) p^{r-1}+1 $$ Remark. The original proposal was the following more general version: Let $n$ be an integer with prime power factorization $q_{1} \cdots q_{m}$. Let $S_{n}$ denote the set of primitive $n$th roots of unity. Find all tuples of nonnegative integers $\left(z_{1}, \ldots, z_{m}\right)$ such that $$ \sum_{\omega \in S_{n}} \frac{f(\omega)}{\left(1-\omega^{n / q_{1}}\right)^{z_{1}} \cdots\left(1-\omega^{n / q_{m}}\right)^{z_{m}}} \in \mathbb{Z} $$ for all polynomials $f \in \mathbb{Z}[x]$. The maximal $z_{i}$ are exponents in the prime ideal factorization of the different ideal of the cyclotomic extension $\mathbb{Q}\left(\zeta_{n}\right) / \mathbb{Q}$. Remark. Let $F=\left(x^{p}-1\right) /(x-1)$ be the minimal polynomial of $\zeta_{p}=e^{2 \pi i / p}$ over $\mathbb{Q}$. A calculation of Euler shows that $$ \left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{p}\right) \in \mathbb{Q}\left[\zeta_{p}\right]: \sum_{\omega \in S_{p}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{p}\right)} \cdot \mathbb{Z}\left[\zeta_{p}\right], $$ where $$ F^{\prime}\left(\zeta_{p}\right)=\frac{p \zeta_{p}^{p-1}-\left[1+\zeta_{p}+\cdots+\zeta_{p}^{p-1}\right]}{1-\zeta_{p}}=p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1} $$ is $\left(1-\zeta_{p}\right)^{[p-1]-1}=\left(1-\zeta_{p}\right)^{p-2}$ times a unit of $\mathbb{Z}\left[\zeta_{p}\right]$. Here, $\left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}$ is the dual lattice of $\mathbb{Z}\left[\zeta_{p}\right]$. Remark. Let $K=\mathbb{Q}(\omega)$, so $(p)$ factors as $(1-\omega)^{p-1}$ in the ring of integers $\mathcal{O}_{K}$ (which, for cyclotomic fields, can be shown to be $\mathbb{Z}[\omega])$. In particular, the ramification index $e$ of $(1-\omega)$ over $p$ is the exponent, $p-1$. Since $e=p-1$ is not divisible by $p$, we have so-called tame ramification. Now by the ramification theory of Dedekind's different ideal, the exponent $z_{1}$ that works when $n=p$ is $e-1=p-2$. Higher prime powers are more interesting because of wild ramification: $p$ divides $\phi\left(p^{r}\right)=$ $p^{r-1}(p-1)$ if and only if $r>1$. (This is a similar phenomena to how Hensel's lemma for $x^{2}-c$ is more interesting mod powers of 2 than mod odd prime powers.) Remark. Let $F=\left(x^{q}-1\right) /\left(x^{q / p}-1\right)$ be the minimal polynomial of $\zeta_{q}=e^{2 \pi i / q}$ over $\mathbb{Q}$. The aforementioned calculation of Euler shows that $$ \left(\mathbb{Z}\left[\zeta_{q}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{q}\right) \in \mathbb{Q}\left[\zeta_{q}\right]: \sum_{\omega \in S_{q}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{q}\right)} \cdot \mathbb{Z}\left[\zeta_{q}\right] $$ where the chain rule implies (using the computation from the prime case) $$ F^{\prime}\left(\zeta_{q}\right)=\left[p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1}\right] \cdot \frac{q}{p} \zeta_{q}^{(q / p)-1}=q\left(1-\zeta_{p}\right)^{-1} \zeta_{q}^{-1} $$ is $\left(1-\zeta_{q}\right)^{r \phi(q)-q / p}=\left(1-\zeta_{q}\right)^{z_{q}}$ times a unit of $\mathbb{Z}\left[\zeta_{q}\right]$.
|
p-1
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Let $q=p^{r}$ for a prime number $p$ and positive integer $r$. Let $\zeta=e^{\frac{2 \pi i}{q}}$. Find the least positive integer $n$ such that $$ \sum_{\substack{1 \leq k \leq q \\ \operatorname{gcd}(k, p)=1}} \frac{1}{\left(1-\zeta^{k}\right)^{n}} $$ is not an integer. (The sum is over all $1 \leq k \leq q$ with $p$ not dividing $k$.)
|
Let $S_{q}$ denote the set of primitive $q$ th roots of unity (thus, the sum in question is a sum over $S_{q}$ ). Solution 2 (Nikolai Beluhov). Suppose that the complex numbers $\frac{1}{1-\omega}$ for $\omega \in S_{q}$ are the roots of $$ P(x)=x^{d}-c_{1} x^{d-1}+c_{2} x^{d-2}-\cdots \pm c_{d} $$ so that $c_{k}$ is their $k$-th elementary symmetric polynomial and $d=\phi(q)=(p-1) p^{r-1}$. Additionally denote $$ S_{n}=\sum_{\omega \in S_{q}} \frac{1}{(1-\omega)^{n}} $$ Then, by Newton's identities, $$ \begin{aligned} S_{1} & =c_{1} \\ S_{2} & =c_{1} S_{1}-2 c_{2} \\ S_{3} & =c_{1} S_{2}-c_{2} S_{1}+3 c_{3} \end{aligned} $$ and so on. The general pattern when $n \leq d$ is $$ S_{n}=\left[\sum_{j=1}^{n-1}(-1)^{j+1} c_{j} S_{n-j}\right]+(-1)^{n+1} n c_{n} $$ After that, when $n>d$, the pattern changes to $$ S_{n}=\sum_{j=1}^{d}(-1)^{j+1} c_{j} S_{n-j} $$ ## Lemma All of the $c_{i}$ are integers except for $c_{d}$. Furthermore, $c_{d}$ is $1 / p$ times an integer. $$ \Phi_{q}(x)=1+x^{p^{r-1}}+x^{2 p^{r-1}}+\cdots+x^{(p-1) p^{r-1}} $$ The polynomial $$ Q(x)=1+(1+x)^{p^{r-1}}+(1+x)^{2 p^{r-1}}+\cdots+(1+x)^{(p-1) p^{r-1}} $$ has roots $\omega-1$ for $\omega \in S_{q}$, so it is equal to $p(-x)^{d} P(-1 / x)$ by comparing constant coefficients. Comparing the remaining coefficients, we find that $c_{n}$ is $1 / p$ times the $x^{n}$ coefficient of $Q$. Since $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$, we conclude that, modulo $p$, $$ \begin{aligned} Q(x) & \equiv 1+\left(1+x^{p^{r-1}}\right)+\left(1+x^{p^{r-1}}\right)^{2}+\cdots+\left(1+x^{p^{r-1}}\right)^{p-1} \\ & \equiv\left[\left(1+x^{p^{r-1}}\right)^{p}-1\right] / x^{p^{r-1}} \end{aligned} $$ Since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, it follows that all coefficients of $Q(x)$ are multiples of $p$ save for the leading one. Therefore, $c_{n}$ is an integer when $n<d$, while $c_{d}$ is $1 / p$ times an integer. By the recurrences above, $S_{n}$ is an integer for $n<d$. When $r=1$, we get that $d c_{d}$ is not an integer, so $S_{d}$ is not an integer, either. Thus the answer for $r=1$ is $n=p-1$. Suppose now that $r \geq 2$. Then $d c_{d}$ does become an integer, so $S_{d}$ is an integer as well. ## Lemma For all $n$ with $1 \leq n \leq d$, we have $\nu_{p}\left(n c_{n}\right) \geq r-2$. Furthermore, the smallest $n$ such that $\nu_{p}\left(n c_{n}\right)=r-2$ is $d-p^{r-1}+1$. $$ p^{r-1}(1+x)^{p^{r-1}-1}\left[\sum_{k=1}^{p-1} k(1+x)^{(k-1) p^{r-1}}\right] . $$ What we want to prove reduces to showing that all coefficients of the polynomial in the square brackets are multiples of $p$ except for the leading one. Using the same trick $(x+y)^{p} \equiv x^{p}+y^{p}(\bmod p)$ as before and also writing $w$ for $x^{p^{r-1}}$, modulo $p$ the polynomial in the square brackets becomes $$ 1+2(1+w)+3(1+w)^{2}+\cdots+(p-1)(1+w)^{p-2} $$ This is the derivative of $$ 1+(1+w)+(1+w)^{2}+\cdots+(1+w)^{p-1}=\left[(1+w)^{p}-1\right] / w $$ and so, since $\binom{p}{j}$ is a multiple of $p$ when $0<j<p$, we are done. Finally, we finish the problem with the following claim. Claim - Let $m=d-p^{r-1}$. Then for all $k \geq 0$ and $1 \leq j \leq d$, we have $$ \begin{aligned} & \nu_{p}\left(S_{k d+m+1}\right)=r-2-k \\ & \nu_{p}\left(S_{k d+m+j}\right) \geq r-2-k \end{aligned} $$ $$ \nu_{p}\left((m+1) c_{m+1}\right)=r-2 $$ and all other terms in the recurrence relation are divisible by $p^{r-1}$. We can similarly check that $\nu_{p}\left(S_{n}\right) \geq r-2$ for $m+1 \leq n \leq d$. Newton's identities combined with the first lemma now imply the following for $n>d$ : - If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right) \geq \ell+1$, then $\nu_{p}\left(S_{n}\right) \geq \ell$. - If $\nu_{p}\left(S_{n-j}\right) \geq \ell$ for all $1 \leq j \leq d$ and $\nu_{p}\left(S_{n-d}\right)=\ell$, then $\nu_{p}\left(S_{n}\right)=\ell-1$. Together, these prove the claim by induction. By the claim, the smallest $n$ for which $\nu_{p}\left(S_{n}\right)<0$ (equivalent to $S_{n}$ not being an integer, by the recurrences) is $$ n=(r-1) d+m+1=((p-1) r-1) p^{r-1}+1 $$ Remark. The original proposal was the following more general version: Let $n$ be an integer with prime power factorization $q_{1} \cdots q_{m}$. Let $S_{n}$ denote the set of primitive $n$th roots of unity. Find all tuples of nonnegative integers $\left(z_{1}, \ldots, z_{m}\right)$ such that $$ \sum_{\omega \in S_{n}} \frac{f(\omega)}{\left(1-\omega^{n / q_{1}}\right)^{z_{1}} \cdots\left(1-\omega^{n / q_{m}}\right)^{z_{m}}} \in \mathbb{Z} $$ for all polynomials $f \in \mathbb{Z}[x]$. The maximal $z_{i}$ are exponents in the prime ideal factorization of the different ideal of the cyclotomic extension $\mathbb{Q}\left(\zeta_{n}\right) / \mathbb{Q}$. Remark. Let $F=\left(x^{p}-1\right) /(x-1)$ be the minimal polynomial of $\zeta_{p}=e^{2 \pi i / p}$ over $\mathbb{Q}$. A calculation of Euler shows that $$ \left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{p}\right) \in \mathbb{Q}\left[\zeta_{p}\right]: \sum_{\omega \in S_{p}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{p}\right)} \cdot \mathbb{Z}\left[\zeta_{p}\right], $$ where $$ F^{\prime}\left(\zeta_{p}\right)=\frac{p \zeta_{p}^{p-1}-\left[1+\zeta_{p}+\cdots+\zeta_{p}^{p-1}\right]}{1-\zeta_{p}}=p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1} $$ is $\left(1-\zeta_{p}\right)^{[p-1]-1}=\left(1-\zeta_{p}\right)^{p-2}$ times a unit of $\mathbb{Z}\left[\zeta_{p}\right]$. Here, $\left(\mathbb{Z}\left[\zeta_{p}\right]\right)^{*}$ is the dual lattice of $\mathbb{Z}\left[\zeta_{p}\right]$. Remark. Let $K=\mathbb{Q}(\omega)$, so $(p)$ factors as $(1-\omega)^{p-1}$ in the ring of integers $\mathcal{O}_{K}$ (which, for cyclotomic fields, can be shown to be $\mathbb{Z}[\omega])$. In particular, the ramification index $e$ of $(1-\omega)$ over $p$ is the exponent, $p-1$. Since $e=p-1$ is not divisible by $p$, we have so-called tame ramification. Now by the ramification theory of Dedekind's different ideal, the exponent $z_{1}$ that works when $n=p$ is $e-1=p-2$. Higher prime powers are more interesting because of wild ramification: $p$ divides $\phi\left(p^{r}\right)=$ $p^{r-1}(p-1)$ if and only if $r>1$. (This is a similar phenomena to how Hensel's lemma for $x^{2}-c$ is more interesting mod powers of 2 than mod odd prime powers.) Remark. Let $F=\left(x^{q}-1\right) /\left(x^{q / p}-1\right)$ be the minimal polynomial of $\zeta_{q}=e^{2 \pi i / q}$ over $\mathbb{Q}$. The aforementioned calculation of Euler shows that $$ \left(\mathbb{Z}\left[\zeta_{q}\right]\right)^{*}:=\left\{\alpha=g\left(\zeta_{q}\right) \in \mathbb{Q}\left[\zeta_{q}\right]: \sum_{\omega \in S_{q}} f(\omega) g(\omega) \in \mathbb{Z} \forall f \in \mathbb{Z}[x]\right\}=\frac{1}{F^{\prime}\left(\zeta_{q}\right)} \cdot \mathbb{Z}\left[\zeta_{q}\right] $$ where the chain rule implies (using the computation from the prime case) $$ F^{\prime}\left(\zeta_{q}\right)=\left[p\left(1-\zeta_{p}\right)^{-1} \zeta_{p}^{p-1}\right] \cdot \frac{q}{p} \zeta_{q}^{(q / p)-1}=q\left(1-\zeta_{p}\right)^{-1} \zeta_{q}^{-1} $$ is $\left(1-\zeta_{q}\right)^{r \phi(q)-q / p}=\left(1-\zeta_{q}\right)^{z_{q}}$ times a unit of $\mathbb{Z}\left[\zeta_{q}\right]$.
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2021"
}
|
Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold: - The sides of each rectangle are parallel to the sides of the unit square. - Each point in $S$ is not in the interior of any rectangle. - Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles. (The interior of a polygon does not contain its boundary.)
|
We claim the answer is $k=2 n+2$. The lower bound is given by picking $$ S=\left\{\left(s_{1}, s_{1}\right),\left(s_{2}, s_{2}\right), \ldots,\left(s_{n}, s_{n}\right)\right\} $$ for some real numbers $0<s_{1}<s_{2}<\cdots<s_{n}<1$. Consider the $4 n$ points $$ S^{\prime}=S+\{(\varepsilon, 0),(0, \varepsilon),(-\varepsilon, 0),(0,-\varepsilon)\} \subset(0,1)^{2} $$ for some sufficiently small $\varepsilon>0$. The four rectangles covering each of $$ \left(s_{1}-\varepsilon, s_{1}\right),\left(s_{1}, s_{1}-\varepsilon\right),\left(s_{n}+\varepsilon, s_{n}\right),\left(s_{n}, s_{n}+\varepsilon\right) $$ cannot cover any other points in $S^{\prime}$; all other rectangles can only cover at most 2 points in $S^{\prime}$, giving a bound of $$ k \geq 4+\frac{\left|S^{\prime}\right|-4}{2}=2 n+2 $$  To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let $$ 0=x_{0}<x_{1}<\cdots<x_{m}<x_{m+1}=1 $$ where $x_{1}, \ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \leq i \leq m$, include the $\left|Y_{i}\right|+1$ rectangles $$ \left(x_{i-1}, x_{i+1}\right) \times\left((0,1) \backslash Y_{i}\right) $$ in the union, and also include $\left(0, x_{1}\right) \times(0,1)$ and $\left(x_{m}, 1\right) \times(0,1)$; this uses $m+n+2$ rectangles.  All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\left\{x_{i}, x_{i+1}\right\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with $$ \left(x_{i}, x_{i+1}\right) \times(y-\varepsilon, y+\varepsilon) $$ for some sufficiently small $\varepsilon>0$ gives a total of $$ (m+n+2)+(n-m)=2 n+2 $$ rectangles.
|
2n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold: - The sides of each rectangle are parallel to the sides of the unit square. - Each point in $S$ is not in the interior of any rectangle. - Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles. (The interior of a polygon does not contain its boundary.)
|
We claim the answer is $k=2 n+2$. The lower bound is given by picking $$ S=\left\{\left(s_{1}, s_{1}\right),\left(s_{2}, s_{2}\right), \ldots,\left(s_{n}, s_{n}\right)\right\} $$ for some real numbers $0<s_{1}<s_{2}<\cdots<s_{n}<1$. Consider the $4 n$ points $$ S^{\prime}=S+\{(\varepsilon, 0),(0, \varepsilon),(-\varepsilon, 0),(0,-\varepsilon)\} \subset(0,1)^{2} $$ for some sufficiently small $\varepsilon>0$. The four rectangles covering each of $$ \left(s_{1}-\varepsilon, s_{1}\right),\left(s_{1}, s_{1}-\varepsilon\right),\left(s_{n}+\varepsilon, s_{n}\right),\left(s_{n}, s_{n}+\varepsilon\right) $$ cannot cover any other points in $S^{\prime}$; all other rectangles can only cover at most 2 points in $S^{\prime}$, giving a bound of $$ k \geq 4+\frac{\left|S^{\prime}\right|-4}{2}=2 n+2 $$  To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let $$ 0=x_{0}<x_{1}<\cdots<x_{m}<x_{m+1}=1 $$ where $x_{1}, \ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \leq i \leq m$, include the $\left|Y_{i}\right|+1$ rectangles $$ \left(x_{i-1}, x_{i+1}\right) \times\left((0,1) \backslash Y_{i}\right) $$ in the union, and also include $\left(0, x_{1}\right) \times(0,1)$ and $\left(x_{m}, 1\right) \times(0,1)$; this uses $m+n+2$ rectangles.  All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\left\{x_{i}, x_{i+1}\right\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with $$ \left(x_{i}, x_{i+1}\right) \times(y-\varepsilon, y+\varepsilon) $$ for some sufficiently small $\varepsilon>0$ gives a total of $$ (m+n+2)+(n-m)=2 n+2 $$ rectangles.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$.  Claim - Line $\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$. $$ A P_{A} \cdot A X=A B \cdot A C \cdot \cos \theta \cos (\angle A-\theta)=A Q_{A} \cdot A Y $$ it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\ell_{A}$ passes through $M_{A}$. $$ \text { Claim }-\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=\measuredangle Y P_{A} Q_{A} $$ Therefore, $$ \frac{\sin \angle\left(M_{A} M_{C}, \ell_{A}\right)}{\sin \angle\left(\ell_{A}, M_{A} M_{B}\right)}=\frac{\sin \angle Y P_{A} Q_{A}}{\sin \angle P_{A} Q_{A} X}=\frac{Y Q_{A}}{X P_{A}}=\frac{B C \sin (\angle C+\theta)}{B C \sin (\angle B+\theta)}=\frac{\sin (\angle C+\theta)}{\sin (\angle B+\theta)}, $$ and we conclude by trig Ceva theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$.  Claim - Line $\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$. $$ A P_{A} \cdot A X=A B \cdot A C \cdot \cos \theta \cos (\angle A-\theta)=A Q_{A} \cdot A Y $$ it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\ell_{A}$ passes through $M_{A}$. $$ \text { Claim }-\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=\measuredangle Y P_{A} Q_{A} $$ Therefore, $$ \frac{\sin \angle\left(M_{A} M_{C}, \ell_{A}\right)}{\sin \angle\left(\ell_{A}, M_{A} M_{B}\right)}=\frac{\sin \angle Y P_{A} Q_{A}}{\sin \angle P_{A} Q_{A} X}=\frac{Y Q_{A}}{X P_{A}}=\frac{B C \sin (\angle C+\theta)}{B C \sin (\angle B+\theta)}=\frac{\sin (\angle C+\theta)}{\sin (\angle B+\theta)}, $$ and we conclude by trig Ceva theorem.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\angle P_{A} D Q_{A}$. Claim - $\left(D P_{A} Q_{A}\right)$ passes through the midpoint $M_{A}$ of $B C$. It follows that $M_{A}$ lies on $\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\left(D P_{A} Q_{A}\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\circ}-\theta-C$, so $\angle O_{A} M_{C} M_{A}=90-\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\triangle M_{A} M_{B} M_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\angle P_{A} D Q_{A}$. Claim - $\left(D P_{A} Q_{A}\right)$ passes through the midpoint $M_{A}$ of $B C$. It follows that $M_{A}$ lies on $\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\left(D P_{A} Q_{A}\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\circ}-\theta-C$, so $\angle O_{A} M_{C} M_{A}=90-\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\triangle M_{A} M_{B} M_{C}$.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
【 Answer. All $N$ such that $t^{2} \leq N<t^{2}+t$ for some positive integer $t$. Solution 1 (local). If $t^{2} \leq N<t^{2}+t$ then the sequence $s_{n}=t n+1$ satisfies both conditions. It remains to show that no other values of $N$ work. Define $a_{n}:=s_{n}-s_{n-1}$, and let $p$ be the minimal period of $\left\{a_{n}\right\}$. For each $k \in \mathbb{Z}_{\geq 0}$, let $f(k)$ be the integer such that $$ s_{f(k)}-s_{k} \leq N<s_{f(k)+1}-s_{k} $$ Note that $f\left(s_{n-1}\right)=s_{n}$ for all $n$. Since $\left\{a_{n}\right\}$ is periodic with period $p, f(k+p)=f(k)+p$ for all $k$, so $k \mapsto f(k)-k$ is periodic with period $p$. We also note that $f$ is nondecreasing: if $k<k^{\prime}$ but $f\left(k^{\prime}\right)<f(k)$ then $$ N<s_{f\left(k^{\prime}\right)+1}-s_{k^{\prime}}<s_{f(k)}-s_{k} \leq N $$ which is absurd. We now claim that $$ \max _{k}(f(k)-k)<p+\min _{k}(f(k)-k) $$ Indeed, if $f\left(k^{\prime}\right)-k^{\prime} \geq p+f(k)-k$ then we can shift $k$ and $k^{\prime}$ so that $0 \leq k-k^{\prime}<p$, and it follows that $k \leq k^{\prime} \leq f\left(k^{\prime}\right)<f(k)$, violating the fact that $f$ is nondecreasing. Therefore $\max _{k}(f(k)-k)<p+\min _{k}(f(k)-k)$, so $f(k)-k$ is uniquely determined by its value modulo $p$. In particular, since $a_{n}=f\left(s_{n-1}\right)-s_{n-1}, a_{n}$ is also uniquely determined by its value modulo $p$, so $\left\{a_{n} \bmod p\right\}$ also has minimal period $p$. Now work in $\mathbb{Z} / p \mathbb{Z}$ and consider the sequence $s_{0}, f\left(s_{0}\right), f\left(f\left(s_{0}\right)\right), \ldots$. This sequence must be eventually periodic; suppose it has minimal period $p^{\prime}$, which must be at most $p$. Then, since $$ f^{n}\left(s_{0}\right)-f^{n-1}\left(s_{0}\right)=s_{n}-s_{n-1}=a_{n} $$ and $\left\{a_{n} \bmod p\right\}$ has minimal period $p$, we must have $p^{\prime}=p$. Therefore the directed graph $G$ on $\mathbb{Z} / p \mathbb{Z}$ given by the edges $k \rightarrow f(k)$ is simply a $p$-cycle, which implies that the map $k \mapsto f(k)$ is a bijection on $\mathbb{Z} / p \mathbb{Z}$. Therefore, $f(k+1) \neq f(k)$ for all $k$ (unless $p=1$, but in this case the following holds anyways), hence $$ f(k)<f(k+1)<\cdots<f(k+p)=f(k)+p $$ This implies $f(k+1)=f(k)+1$ for all $k$, so $f(k)-k$ is constant, therefore $a_{n}=$ $f\left(s_{n-1}\right)-s_{n-1}$ is also constant. Let $a_{n} \equiv t$. It follows that $t^{2} \leq N<t^{2}+t$ as we wanted.
|
t^{2} \leq N < t^{2} + t
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
【 Answer. All $N$ such that $t^{2} \leq N<t^{2}+t$ for some positive integer $t$. Solution 1 (local). If $t^{2} \leq N<t^{2}+t$ then the sequence $s_{n}=t n+1$ satisfies both conditions. It remains to show that no other values of $N$ work. Define $a_{n}:=s_{n}-s_{n-1}$, and let $p$ be the minimal period of $\left\{a_{n}\right\}$. For each $k \in \mathbb{Z}_{\geq 0}$, let $f(k)$ be the integer such that $$ s_{f(k)}-s_{k} \leq N<s_{f(k)+1}-s_{k} $$ Note that $f\left(s_{n-1}\right)=s_{n}$ for all $n$. Since $\left\{a_{n}\right\}$ is periodic with period $p, f(k+p)=f(k)+p$ for all $k$, so $k \mapsto f(k)-k$ is periodic with period $p$. We also note that $f$ is nondecreasing: if $k<k^{\prime}$ but $f\left(k^{\prime}\right)<f(k)$ then $$ N<s_{f\left(k^{\prime}\right)+1}-s_{k^{\prime}}<s_{f(k)}-s_{k} \leq N $$ which is absurd. We now claim that $$ \max _{k}(f(k)-k)<p+\min _{k}(f(k)-k) $$ Indeed, if $f\left(k^{\prime}\right)-k^{\prime} \geq p+f(k)-k$ then we can shift $k$ and $k^{\prime}$ so that $0 \leq k-k^{\prime}<p$, and it follows that $k \leq k^{\prime} \leq f\left(k^{\prime}\right)<f(k)$, violating the fact that $f$ is nondecreasing. Therefore $\max _{k}(f(k)-k)<p+\min _{k}(f(k)-k)$, so $f(k)-k$ is uniquely determined by its value modulo $p$. In particular, since $a_{n}=f\left(s_{n-1}\right)-s_{n-1}, a_{n}$ is also uniquely determined by its value modulo $p$, so $\left\{a_{n} \bmod p\right\}$ also has minimal period $p$. Now work in $\mathbb{Z} / p \mathbb{Z}$ and consider the sequence $s_{0}, f\left(s_{0}\right), f\left(f\left(s_{0}\right)\right), \ldots$. This sequence must be eventually periodic; suppose it has minimal period $p^{\prime}$, which must be at most $p$. Then, since $$ f^{n}\left(s_{0}\right)-f^{n-1}\left(s_{0}\right)=s_{n}-s_{n-1}=a_{n} $$ and $\left\{a_{n} \bmod p\right\}$ has minimal period $p$, we must have $p^{\prime}=p$. Therefore the directed graph $G$ on $\mathbb{Z} / p \mathbb{Z}$ given by the edges $k \rightarrow f(k)$ is simply a $p$-cycle, which implies that the map $k \mapsto f(k)$ is a bijection on $\mathbb{Z} / p \mathbb{Z}$. Therefore, $f(k+1) \neq f(k)$ for all $k$ (unless $p=1$, but in this case the following holds anyways), hence $$ f(k)<f(k+1)<\cdots<f(k+p)=f(k)+p $$ This implies $f(k+1)=f(k)+1$ for all $k$, so $f(k)-k$ is constant, therefore $a_{n}=$ $f\left(s_{n-1}\right)-s_{n-1}$ is also constant. Let $a_{n} \equiv t$. It follows that $t^{2} \leq N<t^{2}+t$ as we wanted.
|
{
"exam": "USA_TSTST",
"problem_label": "3",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
【 Answer. All $N$ such that $t^{2} \leq N<t^{2}+t$ for some positive integer $t$. 【 Solution 2 (global). Define $\left\{a_{n}\right\}$ and $f$ as in the previous solution. We first show that $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$. Suppose the contrary, i.e. that $s_{i} \equiv s_{j}$ $(\bmod p)$ for some $i, j$ with $i<j<i+p$. Then $a_{s_{i}+k}=a_{s_{j}+k}$ for all $k \geq 0$, therefore $s_{s_{i}+k}-s_{s_{i}}=s_{s_{j}+k}-s_{s_{j}}$ for all $k \geq 0$, therefore $$ a_{i+1}=f\left(s_{i}\right)-s_{i}=f\left(s_{j}\right)-s_{j}=a_{j+1} \quad \text { and } \quad s_{i+1}=f\left(s_{i}\right) \equiv f\left(s_{j}\right)=s_{j+1} \quad(\bmod p) $$ Continuing this inductively, we obtain $a_{i+k}=a_{j+k}$ for all $k$, so $\left\{a_{n}\right\}$ has period $j-i<p$, which is a contradiction. Therefore $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$, and this implies that $\left\{s_{i}, \ldots, s_{i+p-1}\right\}$ forms a complete residue system modulo $p$ for all $i$. Consequently we must have $s_{i+p} \equiv s_{i}(\bmod p)$ for all $i$. Let $T=s_{p}-s_{0}=a_{1}+\cdots+a_{p}$. Since $\left\{a_{n}\right\}$ is periodic with period $p$, and $\{i+1, \ldots, i+k p\}$ contains exactly $k$ values of each residue class modulo $p$, $$ s_{i+k p}-s_{i}=a_{i+1}+\cdots+a_{i+k p}=k T $$ for all $i, k$. Since $p \mid T$, it follows that $s_{s_{p}}-s_{s_{0}}=\frac{T}{p} \cdot T=\frac{T^{2}}{p}$. Summing up the inequalities $$ s_{s_{n}}-s_{s_{n-1}} \leq N<s_{s_{n}+1}-s_{s_{n-1}}=s_{s_{n}}-s_{s_{n-1}}+a_{s_{n}+1} $$ for $n \in\{1, \ldots, p\}$ then implies $$ \frac{T^{2}}{p}=s_{s_{p}}-s_{s_{0}} \leq N p<\frac{T^{2}}{p}+a_{s_{1}+1}+a_{s_{2}+1}+\cdots+a_{s_{p}+1}=\frac{T^{2}}{p}+T $$ where the last equality holds because $\left\{s_{1}+1, \ldots, s_{p}+1\right\}$ is a complete residue system modulo $p$. Dividing this by $p$ yields $t^{2} \leq N<t^{2}+t$ for $t:=\frac{T}{p} \in \mathbb{Z}^{+}$. Remark (Author comments). There are some similarities between this problem and IMO 2009/3, mainly that they both involve terms of the form $s_{s_{n}}$ and $s_{s_{n}+1}$ and the sequence $s_{0}, s_{1}, \ldots$ turns out to be an arithmetic progression. Other than this, I don't think knowing about IMO 2009/3 will be that useful on this problem, since in this problem the fact that $\left\{s_{n+1}-s_{n}\right\}$ is periodic is fundamentally important. The motivation for this problem comes from the following scenario: assume we have boxes that can hold some things of total size $\leq N$, and a sequence of things of size $a_{1}, a_{2}, \ldots$ (where $a_{i}:=s_{i+1}-s_{i}$ ). We then greedily pack the things in a sequence of boxes, 'closing' each box when it cannot fit the next thing. The number of things we put in each box gives a sequence $b_{1}, b_{2}, \ldots$. This problem asks when we can have $\left\{a_{n}\right\}=\left\{b_{n}\right\}$, assuming that we start with a sequence $\left\{a_{n}\right\}$ that is periodic. (Extra motivation: I first thought about this scenario when I was pasting some text repeatedly into the Notes app and noticed that the word at the end of lines are also (eventually) periodic.)
|
t^{2} \leq N<t^{2}+t
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $N$ for which there exists a strictly increasing sequence of positive integers $s_{0}<s_{1}<s_{2}<\cdots$ satisfying the following properties: - the sequence $s_{1}-s_{0}, s_{2}-s_{1}, s_{3}-s_{2}, \ldots$ is periodic; and - $s_{s_{n}}-s_{s_{n-1}} \leq N<s_{1+s_{n}}-s_{s_{n-1}}$ for all positive integers $n$.
|
【 Answer. All $N$ such that $t^{2} \leq N<t^{2}+t$ for some positive integer $t$. 【 Solution 2 (global). Define $\left\{a_{n}\right\}$ and $f$ as in the previous solution. We first show that $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$. Suppose the contrary, i.e. that $s_{i} \equiv s_{j}$ $(\bmod p)$ for some $i, j$ with $i<j<i+p$. Then $a_{s_{i}+k}=a_{s_{j}+k}$ for all $k \geq 0$, therefore $s_{s_{i}+k}-s_{s_{i}}=s_{s_{j}+k}-s_{s_{j}}$ for all $k \geq 0$, therefore $$ a_{i+1}=f\left(s_{i}\right)-s_{i}=f\left(s_{j}\right)-s_{j}=a_{j+1} \quad \text { and } \quad s_{i+1}=f\left(s_{i}\right) \equiv f\left(s_{j}\right)=s_{j+1} \quad(\bmod p) $$ Continuing this inductively, we obtain $a_{i+k}=a_{j+k}$ for all $k$, so $\left\{a_{n}\right\}$ has period $j-i<p$, which is a contradiction. Therefore $s_{i} \not \equiv s_{j}(\bmod p)$ for all $i<j<i+p$, and this implies that $\left\{s_{i}, \ldots, s_{i+p-1}\right\}$ forms a complete residue system modulo $p$ for all $i$. Consequently we must have $s_{i+p} \equiv s_{i}(\bmod p)$ for all $i$. Let $T=s_{p}-s_{0}=a_{1}+\cdots+a_{p}$. Since $\left\{a_{n}\right\}$ is periodic with period $p$, and $\{i+1, \ldots, i+k p\}$ contains exactly $k$ values of each residue class modulo $p$, $$ s_{i+k p}-s_{i}=a_{i+1}+\cdots+a_{i+k p}=k T $$ for all $i, k$. Since $p \mid T$, it follows that $s_{s_{p}}-s_{s_{0}}=\frac{T}{p} \cdot T=\frac{T^{2}}{p}$. Summing up the inequalities $$ s_{s_{n}}-s_{s_{n-1}} \leq N<s_{s_{n}+1}-s_{s_{n-1}}=s_{s_{n}}-s_{s_{n-1}}+a_{s_{n}+1} $$ for $n \in\{1, \ldots, p\}$ then implies $$ \frac{T^{2}}{p}=s_{s_{p}}-s_{s_{0}} \leq N p<\frac{T^{2}}{p}+a_{s_{1}+1}+a_{s_{2}+1}+\cdots+a_{s_{p}+1}=\frac{T^{2}}{p}+T $$ where the last equality holds because $\left\{s_{1}+1, \ldots, s_{p}+1\right\}$ is a complete residue system modulo $p$. Dividing this by $p$ yields $t^{2} \leq N<t^{2}+t$ for $t:=\frac{T}{p} \in \mathbb{Z}^{+}$. Remark (Author comments). There are some similarities between this problem and IMO 2009/3, mainly that they both involve terms of the form $s_{s_{n}}$ and $s_{s_{n}+1}$ and the sequence $s_{0}, s_{1}, \ldots$ turns out to be an arithmetic progression. Other than this, I don't think knowing about IMO 2009/3 will be that useful on this problem, since in this problem the fact that $\left\{s_{n+1}-s_{n}\right\}$ is periodic is fundamentally important. The motivation for this problem comes from the following scenario: assume we have boxes that can hold some things of total size $\leq N$, and a sequence of things of size $a_{1}, a_{2}, \ldots$ (where $a_{i}:=s_{i+1}-s_{i}$ ). We then greedily pack the things in a sequence of boxes, 'closing' each box when it cannot fit the next thing. The number of things we put in each box gives a sequence $b_{1}, b_{2}, \ldots$. This problem asks when we can have $\left\{a_{n}\right\}=\left\{b_{n}\right\}$, assuming that we start with a sequence $\left\{a_{n}\right\}$ that is periodic. (Extra motivation: I first thought about this scenario when I was pasting some text repeatedly into the Notes app and noticed that the word at the end of lines are also (eventually) periodic.)
|
{
"exam": "USA_TSTST",
"problem_label": "3",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers $$ f(m+1), f(m+2), \ldots, f(m+f(n)) $$ is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
We start with the following claim: $$ \text { Claim - If } a \mid b \text { then } f(a) \mid f(b) $$ In what follows, let $a \geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \leq a$. However, we also know that exactly one of $f(2), f(3), \ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\{t, t+f(a), t+2 f(a), \ldots\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \leq t \leq 1+f(a)$, and $f(a) \geq 2$ for $a \geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection. Moreover, we now have that $f(a) \mid f(b)$ implies $f(f(a)) \mid f(f(b))$, i.e. $a \mid b$, so $a \mid b$ if and only if $f(a) \mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \neq p$, then from $f(p) \mid f(p q)$ and $f(q) \mid f(p q)$ it follows that $p q \mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers $$ f(m+1), f(m+2), \ldots, f(m+f(n)) $$ is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
We start with the following claim: $$ \text { Claim - If } a \mid b \text { then } f(a) \mid f(b) $$ In what follows, let $a \geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \leq a$. However, we also know that exactly one of $f(2), f(3), \ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\{t, t+f(a), t+2 f(a), \ldots\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \leq t \leq 1+f(a)$, and $f(a) \geq 2$ for $a \geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection. Moreover, we now have that $f(a) \mid f(b)$ implies $f(f(a)) \mid f(f(b))$, i.e. $a \mid b$, so $a \mid b$ if and only if $f(a) \mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \neq p$, then from $f(p) \mid f(p q)$ and $f(q) \mid f(p q)$ it follows that $p q \mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.
|
{
"exam": "USA_TSTST",
"problem_label": "4",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.) In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $\left.A_{2022}\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
The answer is 22 . To prove the lower bound, note that there are $2022 \cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring. Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\ldots, B_{k}$ in $\left\lceil\log _{2} k\right\rceil$ queries. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\lceil k / 2\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \ldots, B_{\lceil k / 2\rceil}$ are red or all of $B_{\lceil k / 2\rceil}, \ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds. Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\leq 2^{k}-1$ points $A_{i}, \ldots, A_{j}$ with $j-i+1 \leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\lceil(j-i+1) / 2\rceil}$. If it is blue, he finishes in $2 \log _{2}\lceil(j-i+1) / 2\rceil \leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\leq 2^{k-1}-1$ points in two queries, at which point we induct.
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.) In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $\left.A_{2022}\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
The answer is 22 . To prove the lower bound, note that there are $2022 \cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring. Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\ldots, B_{k}$ in $\left\lceil\log _{2} k\right\rceil$ queries. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\lceil k / 2\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \ldots, B_{\lceil k / 2\rceil}$ are red or all of $B_{\lceil k / 2\rceil}, \ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds. Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\leq 2^{k}-1$ points $A_{i}, \ldots, A_{j}$ with $j-i+1 \leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\lceil(j-i+1) / 2\rceil}$. If it is blue, he finishes in $2 \log _{2}\lceil(j-i+1) / 2\rceil \leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\leq 2^{k-1}-1$ points in two queries, at which point we induct.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
\ First solution, by author. Let $\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\odot O X_{A} Y_{A}, \odot O B C$ and $\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\odot O$. (The inversion sends $\odot O B C$ to the line $B C$ ). Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\triangle O B C, \triangle O C A, \triangle O A B$ respectively. Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$. Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that $$ \begin{aligned} & d\left(P_{A}, A B\right)=P_{A} B \sin \left(90^{\circ}+\angle C-\angle A\right) \\ & d\left(P_{A}, A C\right)=P_{A} C \sin \left(90^{\circ}+\angle B-\angle A\right) \end{aligned} $$ Hence the symmetric product and trig Ceva finishes the proof. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
\ First solution, by author. Let $\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\odot O X_{A} Y_{A}, \odot O B C$ and $\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\odot O$. (The inversion sends $\odot O B C$ to the line $B C$ ). Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\triangle O B C, \triangle O C A, \triangle O A B$ respectively. Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$. Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that $$ \begin{aligned} & d\left(P_{A}, A B\right)=P_{A} B \sin \left(90^{\circ}+\angle C-\angle A\right) \\ & d\left(P_{A}, A C\right)=P_{A} C \sin \left(90^{\circ}+\angle B-\angle A\right) \end{aligned} $$ Hence the symmetric product and trig Ceva finishes the proof. 
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\triangle A X_{A} Y_{A}$. The key claim is that: Claim $-O_{A} X_{A} Y_{A} O$ is cyclic. $$ \frac{A X_{A}}{A B}=\frac{A H / 2}{A D}=\frac{R \cos A}{A D} $$ and so $$ \frac{A O}{A D}=R \cdot \frac{A X_{A}}{A B \cdot R \cos A}=\frac{A X_{A}}{A E}=\frac{A Y_{A}}{A F} $$ Hence $\angle X_{A} O Y_{A}=180^{\circ}-2 \angle A=180^{\circ}-\angle X_{A} O_{A} Y_{A}$, which proves the claim. Let $P_{A}$ be the circumcenter of $\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\left(O X_{A} Y_{A}\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$.  Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$. Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\triangle A X_{A} Y_{A}$. The key claim is that: Claim $-O_{A} X_{A} Y_{A} O$ is cyclic. $$ \frac{A X_{A}}{A B}=\frac{A H / 2}{A D}=\frac{R \cos A}{A D} $$ and so $$ \frac{A O}{A D}=R \cdot \frac{A X_{A}}{A B \cdot R \cos A}=\frac{A X_{A}}{A E}=\frac{A Y_{A}}{A F} $$ Hence $\angle X_{A} O Y_{A}=180^{\circ}-2 \angle A=180^{\circ}-\angle X_{A} O_{A} Y_{A}$, which proves the claim. Let $P_{A}$ be the circumcenter of $\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\left(O X_{A} Y_{A}\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$.  Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$. Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that $$ 2 \angle A E B=\angle A D B+\angle A C B, $$ and point $F$ lies on segment $B C$ such that $$ 2 \angle D F A=\angle D C A+\angle D B A . $$ Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\prime}$. Now $A B E E^{\prime}$ and $D A F^{\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\prime}$. Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then $$ \angle A S B=\angle A E B=\frac{1}{2}(\angle A D B+\angle A C B)=\frac{1}{2}(\angle A D B+\angle D A C)=\frac{1}{2} \angle A M B, $$ where $M$ is the intersection of $A C$ and $B D$. From $\angle A S B=\frac{1}{2} \angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$. By power of a point, we now obtain $$ C E \cdot C E^{\prime}=C S \cdot C A=C F \cdot C F^{\prime}, $$ from which it follows that $E, F, E^{\prime}$, and $F^{\prime}$ are concyclic. The segments $E E^{\prime}$ and $F F^{\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that $$ 2 \angle A E B=\angle A D B+\angle A C B, $$ and point $F$ lies on segment $B C$ such that $$ 2 \angle D F A=\angle D C A+\angle D B A . $$ Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\prime}$. Now $A B E E^{\prime}$ and $D A F^{\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\prime}$. Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then $$ \angle A S B=\angle A E B=\frac{1}{2}(\angle A D B+\angle A C B)=\frac{1}{2}(\angle A D B+\angle D A C)=\frac{1}{2} \angle A M B, $$ where $M$ is the intersection of $A C$ and $B D$. From $\angle A S B=\frac{1}{2} \angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$. By power of a point, we now obtain $$ C E \cdot C E^{\prime}=C S \cdot C A=C F \cdot C F^{\prime}, $$ from which it follows that $E, F, E^{\prime}$, and $F^{\prime}$ are concyclic. The segments $E E^{\prime}$ and $F F^{\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Find all functions $f: \mathbb{N} \rightarrow \mathbb{Z}$ such that $$ \left\lfloor\frac{f(m n)}{n}\right\rfloor=f(m) $$ for all positive integers $m, n$.
|
There are two families of functions that work: for each $\alpha \in \mathbb{R}$ the function $f(n)=\lfloor\alpha n\rfloor$, and for each $\alpha \in \mathbb{R}$ the function $f(n)=\lceil\alpha n\rceil-1$. (For irrational $\alpha$ these two functions coincide.) It is straightforward to check that these functions indeed work; essentially, this follows from the identity $$ \left\lfloor\frac{\lfloor x n\rfloor}{n}\right\rfloor=\lfloor x\rfloor $$ which holds for all positive integers $n$ and real numbers $x$. We now show that every function that works must be of one of the above forms. Let $f$ be a function that works, and define the sequence $a_{1}, a_{2}, \ldots$ by $a_{n}=f(n!) / n!$. Applying the give condition with $(n!, n+1)$ yields $a_{n+1} \in\left[a_{n}, a_{n}+\frac{1}{n!}\right)$. It follows that the sequence $a_{1}, a_{2}, \ldots$ is non-decreasing and bounded from above by $a_{1}+e$, so this sequence must converge to some limit $\alpha$. If there exists a $k$ such that $a_{k}=\alpha$, then we have $a_{\ell}=\alpha$ for all $\ell>k$. For each positive integer $m$, there exists $\ell>k$ such that $m \mid \ell$ !. Plugging in $m n=\ell$ !, it then follows that $$ f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\lfloor\alpha m\rfloor $$ for all $m$, so $f$ is of the desired form. If there does not exist a $k$ such that $a_{k}=\alpha$, we must have $a_{k}<\alpha$ for all $k$. For each positive integer $m$, we can now pick an $\ell$ such that $m \mid \ell$ ! and $a_{\ell}=\alpha-x$ with $x$ arbitrarily small. It then follows from plugging in $m n=\ell$ ! that $$ f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\left\lfloor\frac{\ell!(\alpha-x)}{\ell!/ m}\right\rfloor=\lfloor\alpha m-m x\rfloor . $$ If $\alpha m$ is an integer we can choose $\ell$ such that $m x<1$, and it follows that $f(m)=\lceil\alpha m\rceil-1$. If $\alpha m$ is not an integer we can choose $\ell$ such that $m x<\{\alpha m\}$, and it also follows that $f(m)=\lceil\alpha m\rceil-1$. We conclude that in this case $f$ is again of the desired form.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all functions $f: \mathbb{N} \rightarrow \mathbb{Z}$ such that $$ \left\lfloor\frac{f(m n)}{n}\right\rfloor=f(m) $$ for all positive integers $m, n$.
|
There are two families of functions that work: for each $\alpha \in \mathbb{R}$ the function $f(n)=\lfloor\alpha n\rfloor$, and for each $\alpha \in \mathbb{R}$ the function $f(n)=\lceil\alpha n\rceil-1$. (For irrational $\alpha$ these two functions coincide.) It is straightforward to check that these functions indeed work; essentially, this follows from the identity $$ \left\lfloor\frac{\lfloor x n\rfloor}{n}\right\rfloor=\lfloor x\rfloor $$ which holds for all positive integers $n$ and real numbers $x$. We now show that every function that works must be of one of the above forms. Let $f$ be a function that works, and define the sequence $a_{1}, a_{2}, \ldots$ by $a_{n}=f(n!) / n!$. Applying the give condition with $(n!, n+1)$ yields $a_{n+1} \in\left[a_{n}, a_{n}+\frac{1}{n!}\right)$. It follows that the sequence $a_{1}, a_{2}, \ldots$ is non-decreasing and bounded from above by $a_{1}+e$, so this sequence must converge to some limit $\alpha$. If there exists a $k$ such that $a_{k}=\alpha$, then we have $a_{\ell}=\alpha$ for all $\ell>k$. For each positive integer $m$, there exists $\ell>k$ such that $m \mid \ell$ !. Plugging in $m n=\ell$ !, it then follows that $$ f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\lfloor\alpha m\rfloor $$ for all $m$, so $f$ is of the desired form. If there does not exist a $k$ such that $a_{k}=\alpha$, we must have $a_{k}<\alpha$ for all $k$. For each positive integer $m$, we can now pick an $\ell$ such that $m \mid \ell$ ! and $a_{\ell}=\alpha-x$ with $x$ arbitrarily small. It then follows from plugging in $m n=\ell$ ! that $$ f(m)=\left\lfloor\frac{f(\ell!)}{\ell!/ m}\right\rfloor=\left\lfloor\frac{\ell!(\alpha-x)}{\ell!/ m}\right\rfloor=\lfloor\alpha m-m x\rfloor . $$ If $\alpha m$ is an integer we can choose $\ell$ such that $m x<1$, and it follows that $f(m)=\lceil\alpha m\rceil-1$. If $\alpha m$ is not an integer we can choose $\ell$ such that $m x<\{\alpha m\}$, and it also follows that $f(m)=\lceil\alpha m\rceil-1$. We conclude that in this case $f$ is again of the desired form.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $k>1$ be a fixed positive integer. Prove that if $n$ is a sufficiently large positive integer, there exists a sequence of integers with the following properties: - Each element of the sequence is between 1 and $n$, inclusive. - For any two different contiguous subsequences of the sequence with length between 2 and $k$ inclusive, the multisets of values in those two subsequences is not the same. - The sequence has length at least $0.499 n^{2}$.
|
For any positive integer $n$, define an $(n, k)$-good sequence to be a finite sequence of integers each between 1 and $n$ inclusive satisfying the second property in the problem statement. The problems asks to show that, for all sufficiently large integers $n$, there is an $(n, k)$-good sequence of length at least $0.499 n^{2}$. Fix $k \geq 2$ and consider some prime power $n=p^{m}$ with $p>k+1$. Consider some $0<g<\frac{n}{k}-1$ with $\operatorname{gcd}(g, n)=1$ and let $a$ be the smallest positive integer with $g^{a} \equiv \pm 1$ $(\bmod n)$. Claim (Main claim) — For $k, n, g, a$ defined as above, there is an $(n, k)$-good sequence of length $a(n+2)+2$. To prove the main claim, we need some results about the structure of $\mathbb{Z} / n \mathbb{Z}$. Specifically, we'll first show that any nontrivial arithmetic sequence is uniquely recoverable. ## Lemma Consider any arithmetic progression of length $i \leq k$ whose common difference is relatively prime to $n$, and let $S$ be the set of residues it takes modulo $n$. Then there exists a unique integer $0<d \leq \frac{n}{2}$ and a unique integer $0 \leq a<n$ such that $$ S=\{a, a+d, \ldots, a+(i-1) d\} $$ - Case $1: i$ is odd, so $i=2 j+1$ for some $j$. Then the middle term of the arithmetic progression is the average of all residues in $S$, which we can uniquely identify as some $u$ (and we know $n$ is coprime to $i$, so it is possible to average the residues). We need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-$ $j d, u-(j-1) d, \ldots, u+j d\}$. Let $X$ be the sum of squares of the residues in $S$, so we have $$ X \equiv(u-j d)^{2}+(u-(j-1) d)^{2}+\cdots+(u+j d)^{2}=(2 j+1) u^{2}+d^{2} \frac{j(j+1)(2 j+1)}{3}, $$ which therefore implies $$ 3\left(X-(2 j+1) u^{2}\right)(j(j+1)(2 j+1))^{-1} \equiv d^{2} $$ thus identifying $d$ uniquely up to sign as desired. - Case 2: $i$ is even, so $i=2 j$ for some $j$. Once again we can compute the average $u$ of the residues in $S$, and we need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-(2 j-1) d, u-(2 j-3) d, \ldots, u+(2 j-1) d\}$. Once again we compute the sum of squares $X$ of the residues in $S$, so that $X \equiv(u-(2 j-1) d)^{2}+(u-(2 j-3) d)^{2}+\cdots+(u+(2 j-1) d)^{2}=2 j u^{2}+\frac{(2 j-1) 2 j(2 j+1)}{3}$ which therefore implies $$ 3\left(X-2 j u^{2}\right)((2 j-1) 2 j(2 j+1))^{-1} \equiv d^{2} $$ again identifying $d$ uniquely up to sign as desired. Thus we have shown that given the set of residues an arithmetic progression takes on modulo $n$, we can recover that progression up to sign. Here we have used the fact that given $d^{2}(\bmod n)$, it is possible to recover $d$ up to $\operatorname{sign}$ provided that $n$ is of the form $p^{m}$ with $p \neq 2$ and $\operatorname{gcd}(d, n)=1$. Now, we will proceed by chaining many arithmetic sequences together. Definition. For any integer $l$ between 0 and $a-1$, inclusive, define $C_{l}$ to be the sequence $0, g^{l}, g^{l}, 2 g^{l}, 3 g^{l}, \ldots,(n-1) g^{l},(n-1) g^{l}$ taken $(\bmod n)$. (This is just a sequence where the $i$ th term is $(i-1) g^{l}$, except the terms $g^{l},(n-1) g^{l}$ is repeated once.) Definition. Consider the sequence $S_{n}$ of residues $\bmod n$ defined as follows: - The first term of $S_{n}$ is 0 . - For each $0 \leq l<a$, the next $n+2$ terms of $S_{n}$ are the terms of $C_{l}$ in order. - The next and final term of $S_{n}$ is 0 . We claim that $S_{n}$ constitutes a $k$-good string with respect to the alphabet of residues modulo $n$. We first make some initial observations about $S_{n}$. ## Lemma $S_{n}$ has the following properties: - $S_{n}$ has length $a(n+2)+2$. - If a contiguous subsequence of $S_{n}$ of length $\leq k$ contains two of the same residue $(\bmod n)$, those two residues occur consecutively in the subsequence. To prove the second property, consider any contiguous subsequence $S_{n}[i: i+k-1]$ of length $k$ which contains two of the same residue modulo $n$. If $S_{n}[i: i+k-1]$ is wholly contained within some $C_{l}$, it's clear that the only way $S_{n}[i: i+k-1]$ could repeat residues if it repeats one of the two consecutive values $g^{l}, g^{l}$ or $(n-1) g^{l},(n-1) g^{l}$, so assume that is not the case. Now, it must be true that $S_{n}[i: i+k-1]$ consists of one contiguous subsequence of the form $$ \left(n-k_{1}\right) g^{l-1},\left(n-\left(k_{1}-1\right)\right) g^{l-1}, \ldots,(n-1) g^{l-1},(n-1) g^{l-1} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l-1}$, and then a second contiguous subsequence of the form $$ 0, g^{l}, g^{l}, 2 g^{l}, \ldots, k_{2} g^{l} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l}$, and we obviously have $k_{2}+k_{1}=k-3$. For $S_{n}[i: i+k-1]$ to contain two of the same residue in non-consecutive positions, there would have to exist some $0<u \leq k_{1}, 0<v \leq k_{2}$ with $(n-u) g^{l-1} \equiv v g^{l}$ $(\bmod n)$, meaning that $u+g v \equiv 0(\bmod n)$. But we know since $k_{1}+k_{2}<k$ that $0<u+g v<k+k g<n$, so this is impossible, as desired. Now we can prove the main claim. First suppose $M$ contains some residue twice. By the last lemma there are only a few possible cases: - $M$ contains multiple copies of the residue 0 . In this case we know $M$ contains the beginning of $S_{n}$, so the corresponding contiguous subsequence is just the first $i$ terms of $S_{n}$. - $M$ contains multiple copies of multiple residues. By the last lemma and the structure of $S_{n}$, we can easily see that $M$ must contain two copies of $-g^{i-1}$ and two copies of $g^{i}$ for some $0 \leq i<a$ that can be identified uniquely, and $M$ must contain portions of both $C_{i-1}, C_{i}$. It follows $M$ 's terms can be partitioned into two portions, the first one being $$ -i_{1} g^{i-1},-\left(i_{1}-1\right) g^{i-1}, \ldots,-g^{i-1},-g^{i-1} $$ and the second one being $$ 0, g^{i}, g^{i}, 2 g^{i}, \ldots, i_{2} g^{i} $$ for some $i_{1}$, $i_{2}$ with $i_{1}+i_{2}=i-3$, and we just need to uniquely identify $i_{1}, i_{2}$. Luckily, by dividing the residues in $M$ by $g^{i-1}$, we know we can partition $M$ 's terms into $$ -i_{1},-\left(i_{1}-1\right), \ldots,-1,-1 $$ as well as $$ 0, g, g, 2 g, \ldots, i_{2} g $$ Now since $i_{2} g \leq k g<n-k$ and $-i_{1} \equiv n-i_{1} \geq n-k$ it is easy to see that $i_{1}, i_{2}$ can be identified uniquely, as desired. - $M$ contains multiple copies of only one residue $g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the beginning of $C_{i}$ and possibly contain the last few terms of $C_{i-1}$, so $M$ must be of the form $g^{i}, g^{i}, 2 g^{i}, \ldots, i_{1} g^{i}$, along with possibly the term 0 or the terms $0,-g^{i-1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $g, g, 2 g, \ldots, i_{1} g$ along with possibly 0 or $0,-1$. Since $i_{1} g \leq k g<n-k$, we can easily disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. - $M$ contains multiple copies of only one residue $-g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the end of $C_{i}$ and possibly the first terms of $C_{i+1}$, so $M$ must be of the form $-g^{i},-g^{i},-2 g^{i}, \ldots,-i_{1} g^{i}$, along with possibly the term 0 or the terms $0, g^{i+1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $-1,-1,-2, \ldots,-i_{1}$, along with possibly 0 or $0, g$. Since $-i_{1} \equiv n-i_{1} \geq \frac{n}{2}$ and $g<\frac{n}{2}$, we can disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. Thus in all cases where $M$ contains a repeated residue, we can identify the unique contiguous subsequence of $S_{n}$ corresponding to $M$. When $M$ does not contain a repeated residue, it follows that $M$ cannot contain both of the $g^{i}$ terms or $(n-1) g^{i}$ terms at the beginning or end of each $C_{i}$. It follows that $M$ is either entirely contained in some $C_{i}$ or contained in the union of the end of some $C_{i}$ with the beginning of some $C_{i+1}$, meaning $M$ corresponds to a contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$. In the first case, since each $C_{i}$ is an arithmetic progression when the repeated terms are ignored, Lemma 1 implies that we can uniquely determine the location of $M$, and in the second case, it is easy to tell which contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$ corresponds to $M$. Therefore, in all cases, for any multiset $M$ corresponding to some contiguous subsequence of $S_{n}$ of length $i \leq k$, we can uniquely identify the contiguous subsequence, meaning $S_{n}$ is $k$-good with respect to the alphabet of residues modulo $n$, as desired. Now we will finish the problem. We observe the following. Claim - Fix $k$ and let $p>k+1$ be a prime. Then for $n=p^{2}$ we can find a $(n, k)$-good sequence of length $\frac{p(p-1)\left(p^{2}+2\right)}{2}$. We will prove a stronger statement that $g<p$. Indeed, consider any primitive root $g_{0}$ $(\bmod p)$. Then $g_{0}+a p$ has order $p-1 \operatorname{modulo} p$, so its order modulo $p^{2}$ is divisible by $p-1$, hence $g_{0}+a p$ is a primitive root modulo $p^{2}$ as long as $\left(g_{0}+a p\right)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. Now $$ \left(g_{0}+a p\right)^{p-1}=\sum_{i} g_{0}^{p-1-i}(a p)^{i}\binom{p-1}{i} \equiv g_{0}^{p-1}+g_{0}^{p-2}(a p) \quad\left(\bmod p^{2}\right) $$ In particular, of the values $g_{0}, g_{0}+p, \ldots, g_{0}+p(p-1)$, only one has order $p-1$ and the rest are primitive roots. So for each $0<g_{0}<p$ which is a primitive root modulo $p$, either $g_{0}$ is a primitive root modulo $p^{2}$ or $g_{0}$ has order $p-1$ but $g_{0}+p, g_{0}+2 p, \ldots, g_{0}+p(p-1)$ are all primitive roots. By considering all choices of $g_{0}$, we either find a primitive root $\left(\bmod p^{2}\right)$ which is between 0 and $p$, or we find that all residues $\left(\bmod p^{2}\right)$ of order $p-1$ are between 0 and $p$. But if $\operatorname{ord}_{p^{2}}(a)=p-1$ then $\operatorname{ord}_{p^{2}}\left(a^{-1}\right)=p-1$, and two residues between $0, p$ cannot be inverses modulo $p^{2}$ (because with the exception of 1 , they cannot multiply to something $\geq p^{2}+1$ ), so there is always a primitive root between $0, p$ as desired. Now for arbitrarily large $n$ we can choose $p<\sqrt{n}$ with $\frac{p}{\sqrt{n}}$ arbitrarily close to 1 ; by the previous claim, we can get an $(n, k)$-good sequence of length at least $\frac{p-1}{p} \cdot \frac{p^{4}}{2}$ for any constant, so for sufficiently large $n, p$ we get $(n, k)$-good sequences of length $0.499 n^{2}$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Let $k>1$ be a fixed positive integer. Prove that if $n$ is a sufficiently large positive integer, there exists a sequence of integers with the following properties: - Each element of the sequence is between 1 and $n$, inclusive. - For any two different contiguous subsequences of the sequence with length between 2 and $k$ inclusive, the multisets of values in those two subsequences is not the same. - The sequence has length at least $0.499 n^{2}$.
|
For any positive integer $n$, define an $(n, k)$-good sequence to be a finite sequence of integers each between 1 and $n$ inclusive satisfying the second property in the problem statement. The problems asks to show that, for all sufficiently large integers $n$, there is an $(n, k)$-good sequence of length at least $0.499 n^{2}$. Fix $k \geq 2$ and consider some prime power $n=p^{m}$ with $p>k+1$. Consider some $0<g<\frac{n}{k}-1$ with $\operatorname{gcd}(g, n)=1$ and let $a$ be the smallest positive integer with $g^{a} \equiv \pm 1$ $(\bmod n)$. Claim (Main claim) — For $k, n, g, a$ defined as above, there is an $(n, k)$-good sequence of length $a(n+2)+2$. To prove the main claim, we need some results about the structure of $\mathbb{Z} / n \mathbb{Z}$. Specifically, we'll first show that any nontrivial arithmetic sequence is uniquely recoverable. ## Lemma Consider any arithmetic progression of length $i \leq k$ whose common difference is relatively prime to $n$, and let $S$ be the set of residues it takes modulo $n$. Then there exists a unique integer $0<d \leq \frac{n}{2}$ and a unique integer $0 \leq a<n$ such that $$ S=\{a, a+d, \ldots, a+(i-1) d\} $$ - Case $1: i$ is odd, so $i=2 j+1$ for some $j$. Then the middle term of the arithmetic progression is the average of all residues in $S$, which we can uniquely identify as some $u$ (and we know $n$ is coprime to $i$, so it is possible to average the residues). We need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-$ $j d, u-(j-1) d, \ldots, u+j d\}$. Let $X$ be the sum of squares of the residues in $S$, so we have $$ X \equiv(u-j d)^{2}+(u-(j-1) d)^{2}+\cdots+(u+j d)^{2}=(2 j+1) u^{2}+d^{2} \frac{j(j+1)(2 j+1)}{3}, $$ which therefore implies $$ 3\left(X-(2 j+1) u^{2}\right)(j(j+1)(2 j+1))^{-1} \equiv d^{2} $$ thus identifying $d$ uniquely up to sign as desired. - Case 2: $i$ is even, so $i=2 j$ for some $j$. Once again we can compute the average $u$ of the residues in $S$, and we need to show that there is only one choice of $d$, up to $\pm$, so that $S=\{u-(2 j-1) d, u-(2 j-3) d, \ldots, u+(2 j-1) d\}$. Once again we compute the sum of squares $X$ of the residues in $S$, so that $X \equiv(u-(2 j-1) d)^{2}+(u-(2 j-3) d)^{2}+\cdots+(u+(2 j-1) d)^{2}=2 j u^{2}+\frac{(2 j-1) 2 j(2 j+1)}{3}$ which therefore implies $$ 3\left(X-2 j u^{2}\right)((2 j-1) 2 j(2 j+1))^{-1} \equiv d^{2} $$ again identifying $d$ uniquely up to sign as desired. Thus we have shown that given the set of residues an arithmetic progression takes on modulo $n$, we can recover that progression up to sign. Here we have used the fact that given $d^{2}(\bmod n)$, it is possible to recover $d$ up to $\operatorname{sign}$ provided that $n$ is of the form $p^{m}$ with $p \neq 2$ and $\operatorname{gcd}(d, n)=1$. Now, we will proceed by chaining many arithmetic sequences together. Definition. For any integer $l$ between 0 and $a-1$, inclusive, define $C_{l}$ to be the sequence $0, g^{l}, g^{l}, 2 g^{l}, 3 g^{l}, \ldots,(n-1) g^{l},(n-1) g^{l}$ taken $(\bmod n)$. (This is just a sequence where the $i$ th term is $(i-1) g^{l}$, except the terms $g^{l},(n-1) g^{l}$ is repeated once.) Definition. Consider the sequence $S_{n}$ of residues $\bmod n$ defined as follows: - The first term of $S_{n}$ is 0 . - For each $0 \leq l<a$, the next $n+2$ terms of $S_{n}$ are the terms of $C_{l}$ in order. - The next and final term of $S_{n}$ is 0 . We claim that $S_{n}$ constitutes a $k$-good string with respect to the alphabet of residues modulo $n$. We first make some initial observations about $S_{n}$. ## Lemma $S_{n}$ has the following properties: - $S_{n}$ has length $a(n+2)+2$. - If a contiguous subsequence of $S_{n}$ of length $\leq k$ contains two of the same residue $(\bmod n)$, those two residues occur consecutively in the subsequence. To prove the second property, consider any contiguous subsequence $S_{n}[i: i+k-1]$ of length $k$ which contains two of the same residue modulo $n$. If $S_{n}[i: i+k-1]$ is wholly contained within some $C_{l}$, it's clear that the only way $S_{n}[i: i+k-1]$ could repeat residues if it repeats one of the two consecutive values $g^{l}, g^{l}$ or $(n-1) g^{l},(n-1) g^{l}$, so assume that is not the case. Now, it must be true that $S_{n}[i: i+k-1]$ consists of one contiguous subsequence of the form $$ \left(n-k_{1}\right) g^{l-1},\left(n-\left(k_{1}-1\right)\right) g^{l-1}, \ldots,(n-1) g^{l-1},(n-1) g^{l-1} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l-1}$, and then a second contiguous subsequence of the form $$ 0, g^{l}, g^{l}, 2 g^{l}, \ldots, k_{2} g^{l} $$ which are the portions of $S_{n}[i: i+k-1]$ contained in $C_{l}$, and we obviously have $k_{2}+k_{1}=k-3$. For $S_{n}[i: i+k-1]$ to contain two of the same residue in non-consecutive positions, there would have to exist some $0<u \leq k_{1}, 0<v \leq k_{2}$ with $(n-u) g^{l-1} \equiv v g^{l}$ $(\bmod n)$, meaning that $u+g v \equiv 0(\bmod n)$. But we know since $k_{1}+k_{2}<k$ that $0<u+g v<k+k g<n$, so this is impossible, as desired. Now we can prove the main claim. First suppose $M$ contains some residue twice. By the last lemma there are only a few possible cases: - $M$ contains multiple copies of the residue 0 . In this case we know $M$ contains the beginning of $S_{n}$, so the corresponding contiguous subsequence is just the first $i$ terms of $S_{n}$. - $M$ contains multiple copies of multiple residues. By the last lemma and the structure of $S_{n}$, we can easily see that $M$ must contain two copies of $-g^{i-1}$ and two copies of $g^{i}$ for some $0 \leq i<a$ that can be identified uniquely, and $M$ must contain portions of both $C_{i-1}, C_{i}$. It follows $M$ 's terms can be partitioned into two portions, the first one being $$ -i_{1} g^{i-1},-\left(i_{1}-1\right) g^{i-1}, \ldots,-g^{i-1},-g^{i-1} $$ and the second one being $$ 0, g^{i}, g^{i}, 2 g^{i}, \ldots, i_{2} g^{i} $$ for some $i_{1}$, $i_{2}$ with $i_{1}+i_{2}=i-3$, and we just need to uniquely identify $i_{1}, i_{2}$. Luckily, by dividing the residues in $M$ by $g^{i-1}$, we know we can partition $M$ 's terms into $$ -i_{1},-\left(i_{1}-1\right), \ldots,-1,-1 $$ as well as $$ 0, g, g, 2 g, \ldots, i_{2} g $$ Now since $i_{2} g \leq k g<n-k$ and $-i_{1} \equiv n-i_{1} \geq n-k$ it is easy to see that $i_{1}, i_{2}$ can be identified uniquely, as desired. - $M$ contains multiple copies of only one residue $g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the beginning of $C_{i}$ and possibly contain the last few terms of $C_{i-1}$, so $M$ must be of the form $g^{i}, g^{i}, 2 g^{i}, \ldots, i_{1} g^{i}$, along with possibly the term 0 or the terms $0,-g^{i-1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $g, g, 2 g, \ldots, i_{1} g$ along with possibly 0 or $0,-1$. Since $i_{1} g \leq k g<n-k$, we can easily disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. - $M$ contains multiple copies of only one residue $-g^{i}$, for some $0 \leq i<a$ that can be identified uniquely. Then by the last lemma $M$ must be located at the end of $C_{i}$ and possibly the first terms of $C_{i+1}$, so $M$ must be of the form $-g^{i},-g^{i},-2 g^{i}, \ldots,-i_{1} g^{i}$, along with possibly the term 0 or the terms $0, g^{i+1}$. So when we divide $M$ by $g^{i-1}$ we should be left with terms of the form $-1,-1,-2, \ldots,-i_{1}$, along with possibly 0 or $0, g$. Since $-i_{1} \equiv n-i_{1} \geq \frac{n}{2}$ and $g<\frac{n}{2}$, we can disambiguate these cases and uniquely identify the contiguous subsequence corresponding to $M$. Thus in all cases where $M$ contains a repeated residue, we can identify the unique contiguous subsequence of $S_{n}$ corresponding to $M$. When $M$ does not contain a repeated residue, it follows that $M$ cannot contain both of the $g^{i}$ terms or $(n-1) g^{i}$ terms at the beginning or end of each $C_{i}$. It follows that $M$ is either entirely contained in some $C_{i}$ or contained in the union of the end of some $C_{i}$ with the beginning of some $C_{i+1}$, meaning $M$ corresponds to a contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$. In the first case, since each $C_{i}$ is an arithmetic progression when the repeated terms are ignored, Lemma 1 implies that we can uniquely determine the location of $M$, and in the second case, it is easy to tell which contiguous subsequence of $\left(-g^{i}, 0, g^{i+1}\right)$ corresponds to $M$. Therefore, in all cases, for any multiset $M$ corresponding to some contiguous subsequence of $S_{n}$ of length $i \leq k$, we can uniquely identify the contiguous subsequence, meaning $S_{n}$ is $k$-good with respect to the alphabet of residues modulo $n$, as desired. Now we will finish the problem. We observe the following. Claim - Fix $k$ and let $p>k+1$ be a prime. Then for $n=p^{2}$ we can find a $(n, k)$-good sequence of length $\frac{p(p-1)\left(p^{2}+2\right)}{2}$. We will prove a stronger statement that $g<p$. Indeed, consider any primitive root $g_{0}$ $(\bmod p)$. Then $g_{0}+a p$ has order $p-1 \operatorname{modulo} p$, so its order modulo $p^{2}$ is divisible by $p-1$, hence $g_{0}+a p$ is a primitive root modulo $p^{2}$ as long as $\left(g_{0}+a p\right)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. Now $$ \left(g_{0}+a p\right)^{p-1}=\sum_{i} g_{0}^{p-1-i}(a p)^{i}\binom{p-1}{i} \equiv g_{0}^{p-1}+g_{0}^{p-2}(a p) \quad\left(\bmod p^{2}\right) $$ In particular, of the values $g_{0}, g_{0}+p, \ldots, g_{0}+p(p-1)$, only one has order $p-1$ and the rest are primitive roots. So for each $0<g_{0}<p$ which is a primitive root modulo $p$, either $g_{0}$ is a primitive root modulo $p^{2}$ or $g_{0}$ has order $p-1$ but $g_{0}+p, g_{0}+2 p, \ldots, g_{0}+p(p-1)$ are all primitive roots. By considering all choices of $g_{0}$, we either find a primitive root $\left(\bmod p^{2}\right)$ which is between 0 and $p$, or we find that all residues $\left(\bmod p^{2}\right)$ of order $p-1$ are between 0 and $p$. But if $\operatorname{ord}_{p^{2}}(a)=p-1$ then $\operatorname{ord}_{p^{2}}\left(a^{-1}\right)=p-1$, and two residues between $0, p$ cannot be inverses modulo $p^{2}$ (because with the exception of 1 , they cannot multiply to something $\geq p^{2}+1$ ), so there is always a primitive root between $0, p$ as desired. Now for arbitrarily large $n$ we can choose $p<\sqrt{n}$ with $\frac{p}{\sqrt{n}}$ arbitrarily close to 1 ; by the previous claim, we can get an $(n, k)$-good sequence of length at least $\frac{p-1}{p} \cdot \frac{p^{4}}{2}$ for any constant, so for sufficiently large $n, p$ we get $(n, k)$-good sequences of length $0.499 n^{2}$.
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2022"
}
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 【 Solution 1 using power of a point. From the given condition that $\measuredangle A C R=\measuredangle C G M$, we get that $$ M A^{2}=M C^{2}=M G \cdot M R \Longrightarrow \measuredangle R A C=\measuredangle M G A $$ Analogously, $$ \measuredangle B A S=\measuredangle A G N $$ Hence, $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle M G A+\measuredangle A G N=\measuredangle M G N=\measuredangle B G C . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 【 Solution 1 using power of a point. From the given condition that $\measuredangle A C R=\measuredangle C G M$, we get that $$ M A^{2}=M C^{2}=M G \cdot M R \Longrightarrow \measuredangle R A C=\measuredangle M G A $$ Analogously, $$ \measuredangle B A S=\measuredangle A G N $$ Hence, $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle M G A+\measuredangle A G N=\measuredangle M G N=\measuredangle B G C . $$
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 2 using similar triangles. As before, $\triangle M G C \sim \triangle M C R$ and $\triangle N G B \sim$ $\triangle N B S$. We obtain $$ \frac{|A C|}{|C R|}=\frac{2|M C|}{|C R|}=\frac{2|M G|}{|G C|}=\frac{|G B|}{2|N G|}=\frac{|B S|}{2|B N|}=\frac{|B S|}{|A B|} $$ which together with $\angle A C R=\angle A B S$ yields $$ \triangle A C R \sim \triangle S B A \Longrightarrow \measuredangle B A S=\measuredangle C R A $$ Hence $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle R A C+\measuredangle C R A=-\measuredangle A C R=\measuredangle B G C, $$ which proves the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 2 using similar triangles. As before, $\triangle M G C \sim \triangle M C R$ and $\triangle N G B \sim$ $\triangle N B S$. We obtain $$ \frac{|A C|}{|C R|}=\frac{2|M C|}{|C R|}=\frac{2|M G|}{|G C|}=\frac{|G B|}{2|N G|}=\frac{|B S|}{2|B N|}=\frac{|B S|}{|A B|} $$ which together with $\angle A C R=\angle A B S$ yields $$ \triangle A C R \sim \triangle S B A \Longrightarrow \measuredangle B A S=\measuredangle C R A $$ Hence $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle R A C+\measuredangle C R A=-\measuredangle A C R=\measuredangle B G C, $$ which proves the statement.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms.  Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic. Thus from $\overline{P C} \| \overline{G A}$ we get $$ \measuredangle R A C=\measuredangle R P C=\measuredangle G P C=\measuredangle P G A $$ and similarly $$ \measuredangle B A S=\measuredangle B Q S=\measuredangle B Q G=\measuredangle A G Q $$ We conclude that $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle P G A+\measuredangle A G Q=\measuredangle P G Q=\measuredangle B G C $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms.  Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic. Thus from $\overline{P C} \| \overline{G A}$ we get $$ \measuredangle R A C=\measuredangle R P C=\measuredangle G P C=\measuredangle P G A $$ and similarly $$ \measuredangle B A S=\measuredangle B Q S=\measuredangle B Q G=\measuredangle A G Q $$ We conclude that $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle P G A+\measuredangle A G Q=\measuredangle P G Q=\measuredangle B G C $$
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since $$ \measuredangle C A K=\measuredangle A C R=\measuredangle C G B=\measuredangle C G K, $$ it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic.  Finally, observe that $$ \begin{aligned} \angle R A S+\angle B A C & =\measuredangle B A S+\measuredangle R A C \\ & =\measuredangle A B L+\measuredangle K C A \\ & =\measuredangle A G L+\measuredangle K G A \\ & =\measuredangle K G L \\ & =\angle B G C \end{aligned} $$ as requested.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since $$ \measuredangle C A K=\measuredangle A C R=\measuredangle C G B=\measuredangle C G K, $$ it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic.  Finally, observe that $$ \begin{aligned} \angle R A S+\angle B A C & =\measuredangle B A S+\measuredangle R A C \\ & =\measuredangle A B L+\measuredangle K C A \\ & =\measuredangle A G L+\measuredangle K G A \\ & =\measuredangle K G L \\ & =\angle B G C \end{aligned} $$ as requested.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 『 Solution 5 using complex numbers, by Milan Haiman. Note that $\angle R A S+\angle B A C=$ $\angle B A S+\angle R A C$. We compute $\angle B A S$ in complex numbers; then $\angle R A C$ will then be known by symmetry. Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$. ## Claim - We have $$ \frac{s-a}{b-a}=\frac{a b-2 b c+c a}{2 a b-b c-c a} . $$ $$ s=\frac{a+b}{2}+t(c-g) $$ for some $t \in \mathbb{R}$. By the given angle condition, we have that $$ \frac{(s-b) /(b-a)}{(c-g) /(g-b)} \in \mathbb{R} $$ Note that $$ \frac{s-b}{b-a}=t \frac{c-g}{b-a}-\frac{1}{2} $$ So, $$ t \frac{g-b}{b-a}-\frac{g-b}{2(c-g)} \in \mathbb{R} $$ Thus $$ t=\frac{\operatorname{Im}\left(\frac{g-b}{2(c-g)}\right)}{\operatorname{Im}\left(\frac{g-b}{b-a}\right)}=\frac{1}{2} \cdot \frac{\left(\frac{g-b}{c-g}\right)-\overline{\left(\frac{g-b}{c-g}\right)}}{\left(\frac{g-b}{b-a}\right)-\overline{\left(\frac{g-b}{b-a}\right)}} $$ Let $N$ and $D$ be the numerator and denominator of the second factor above. We want to compute $$ \frac{s-a}{b-a}=\frac{1}{2}+t \frac{c-g}{b-a}=\frac{(b-a)+2 t(c-g)}{2(b-a)}=\frac{(b-a) D+(c-g) N}{2(b-a) D} $$ We have $$ \begin{aligned} (c-g) N & =g-b-(c-g) \overline{\left(\frac{g-b}{c-g}\right)} \\ & =\frac{a+b+c}{3}-b-\left(c-\frac{a+b+c}{3}\right) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{c}-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}} \\ & =\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\ & =\frac{3\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\right)}{3(2 a b-b c-c a)} \\ & =\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a} \end{aligned} $$ We also compute $$ \begin{aligned} (b-a) D & =g-b-(b-a) \overline{\left(\frac{g-b}{b-a}\right)} \\ & =\frac{a+b+c}{3}-b-(b-a) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{b}-\frac{3}{a}} \\ & =\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\ & =\frac{a b-b c-c a+c^{2}}{3 c} \\ & =\frac{(a-c)(b-c)}{3 c} \end{aligned} $$ So, we obtain $$ \frac{s-a}{b-a}=\frac{\frac{1}{3 c}+\frac{a-b}{2 a b-b c-c a}}{\frac{2}{3 c}}=\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\frac{a b-2 b c+c a}{2 a b-b c-c a} $$ By symmetry, $$ \frac{r-a}{c-a}=\frac{a b-2 b c+c a}{2 c a-a b-b c} $$ Hence their ratio $$ \frac{s-a}{b-a} \div \frac{r-a}{c-a}=\frac{2 a b-b c-c a}{2 c a-a b-b c} $$ has argument $\angle R A C+\angle B A S$. We also have that $\angle B G C$ is the argument of $$ \frac{b-g}{c-g}=\frac{2 b-a-c}{2 c-a-b} $$ Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 『 Solution 5 using complex numbers, by Milan Haiman. Note that $\angle R A S+\angle B A C=$ $\angle B A S+\angle R A C$. We compute $\angle B A S$ in complex numbers; then $\angle R A C$ will then be known by symmetry. Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$. ## Claim - We have $$ \frac{s-a}{b-a}=\frac{a b-2 b c+c a}{2 a b-b c-c a} . $$ $$ s=\frac{a+b}{2}+t(c-g) $$ for some $t \in \mathbb{R}$. By the given angle condition, we have that $$ \frac{(s-b) /(b-a)}{(c-g) /(g-b)} \in \mathbb{R} $$ Note that $$ \frac{s-b}{b-a}=t \frac{c-g}{b-a}-\frac{1}{2} $$ So, $$ t \frac{g-b}{b-a}-\frac{g-b}{2(c-g)} \in \mathbb{R} $$ Thus $$ t=\frac{\operatorname{Im}\left(\frac{g-b}{2(c-g)}\right)}{\operatorname{Im}\left(\frac{g-b}{b-a}\right)}=\frac{1}{2} \cdot \frac{\left(\frac{g-b}{c-g}\right)-\overline{\left(\frac{g-b}{c-g}\right)}}{\left(\frac{g-b}{b-a}\right)-\overline{\left(\frac{g-b}{b-a}\right)}} $$ Let $N$ and $D$ be the numerator and denominator of the second factor above. We want to compute $$ \frac{s-a}{b-a}=\frac{1}{2}+t \frac{c-g}{b-a}=\frac{(b-a)+2 t(c-g)}{2(b-a)}=\frac{(b-a) D+(c-g) N}{2(b-a) D} $$ We have $$ \begin{aligned} (c-g) N & =g-b-(c-g) \overline{\left(\frac{g-b}{c-g}\right)} \\ & =\frac{a+b+c}{3}-b-\left(c-\frac{a+b+c}{3}\right) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{c}-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}} \\ & =\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\ & =\frac{3\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\right)}{3(2 a b-b c-c a)} \\ & =\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a} \end{aligned} $$ We also compute $$ \begin{aligned} (b-a) D & =g-b-(b-a) \overline{\left(\frac{g-b}{b-a}\right)} \\ & =\frac{a+b+c}{3}-b-(b-a) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{b}-\frac{3}{a}} \\ & =\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\ & =\frac{a b-b c-c a+c^{2}}{3 c} \\ & =\frac{(a-c)(b-c)}{3 c} \end{aligned} $$ So, we obtain $$ \frac{s-a}{b-a}=\frac{\frac{1}{3 c}+\frac{a-b}{2 a b-b c-c a}}{\frac{2}{3 c}}=\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\frac{a b-2 b c+c a}{2 a b-b c-c a} $$ By symmetry, $$ \frac{r-a}{c-a}=\frac{a b-2 b c+c a}{2 c a-a b-b c} $$ Hence their ratio $$ \frac{s-a}{b-a} \div \frac{r-a}{c-a}=\frac{2 a b-b c-c a}{2 c a-a b-b c} $$ has argument $\angle R A C+\angle B A S$. We also have that $\angle B G C$ is the argument of $$ \frac{b-g}{c-g}=\frac{2 b-a-c}{2 c-a-b} $$ Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 First solution (authors). By Cauchy-Schwarz, we have $$ \begin{aligned} \sum_{k=m}^{n} \frac{k+1}{k^{3}} & =\sum_{k=m}^{n} \frac{\left(\frac{1}{k^{2}}\right)^{2}}{\frac{1}{k(k+1)}} \\ & \geq \frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m(m+1)}+\frac{1}{(m+1)(m+2)}+\cdots+\frac{1}{n(n+1)}} \\ & =\frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m}-\frac{1}{n+1}} \\ & >\frac{\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}}{\frac{1}{m}} \end{aligned} $$ as desired. Remark (Bound on error). Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get $$ A+B-m A^{2}=m \cdot \sum_{m \leq a<b} \frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)} $$ We can upper bound this error by $$ \leq m \cdot \sum_{m \leq a<b} \frac{1}{a^{3}(a+1) b(b+1)}=m \cdot \sum_{m \leq a} \frac{1}{a^{3}(a+1)^{2}} \approx m \cdot \frac{1}{m^{4}}=\frac{1}{m^{3}}, $$ which is still generous as $(a-b)^{2} \ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\frac{1}{10 \mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies $$ m A^{2}+O(B / m)>A+B $$ Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial anyways. My first attempt was the not-so-amazing inequality $$ \frac{n^{2}+3 n}{2}=\sum_{1}^{n} i+1=\sum_{1}^{n} \frac{\frac{1}{i}}{\frac{1}{i(i+1)}}>\left(\sum_{1}^{n} \frac{1}{\sqrt{i}}\right)^{2} $$ which is really not surprising given that $\sum \frac{1}{\sqrt{i}} \ll \frac{n}{\sqrt{2}}$. The key here is that we need "near-equality" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators. This motivates using $\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem. The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\frac{1}{i^{2}} \approx \frac{1}{i(i+1)}$ to be fully exploited.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 First solution (authors). By Cauchy-Schwarz, we have $$ \begin{aligned} \sum_{k=m}^{n} \frac{k+1}{k^{3}} & =\sum_{k=m}^{n} \frac{\left(\frac{1}{k^{2}}\right)^{2}}{\frac{1}{k(k+1)}} \\ & \geq \frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m(m+1)}+\frac{1}{(m+1)(m+2)}+\cdots+\frac{1}{n(n+1)}} \\ & =\frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m}-\frac{1}{n+1}} \\ & >\frac{\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}}{\frac{1}{m}} \end{aligned} $$ as desired. Remark (Bound on error). Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get $$ A+B-m A^{2}=m \cdot \sum_{m \leq a<b} \frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)} $$ We can upper bound this error by $$ \leq m \cdot \sum_{m \leq a<b} \frac{1}{a^{3}(a+1) b(b+1)}=m \cdot \sum_{m \leq a} \frac{1}{a^{3}(a+1)^{2}} \approx m \cdot \frac{1}{m^{4}}=\frac{1}{m^{3}}, $$ which is still generous as $(a-b)^{2} \ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\frac{1}{10 \mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies $$ m A^{2}+O(B / m)>A+B $$ Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial anyways. My first attempt was the not-so-amazing inequality $$ \frac{n^{2}+3 n}{2}=\sum_{1}^{n} i+1=\sum_{1}^{n} \frac{\frac{1}{i}}{\frac{1}{i(i+1)}}>\left(\sum_{1}^{n} \frac{1}{\sqrt{i}}\right)^{2} $$ which is really not surprising given that $\sum \frac{1}{\sqrt{i}} \ll \frac{n}{\sqrt{2}}$. The key here is that we need "near-equality" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators. This motivates using $\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem. The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\frac{1}{i^{2}} \approx \frac{1}{i(i+1)}$ to be fully exploited.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\frac{m+1}{m^{3}}$ and the right side is $\frac{m}{m^{4}}=\frac{1}{m^{3}}$. For the inductive step, suppose we have shown the result for $m+1$. Let $$ A=\sum_{k=m+1}^{n} \frac{1}{k^{2}} \quad \text { and } \quad B=\sum_{k=m+1}^{n} \frac{1}{k^{3}} $$ We know $A+B \geq(m+1) A^{2}$, and we want to show $$ \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right) \geq m\left(A+\frac{1}{m^{2}}\right)^{2} $$ Indeed, $$ \begin{aligned} \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right)-m\left(A+\frac{1}{m^{2}}\right)^{2} & =A+B+\frac{m+1}{m^{3}}-m A^{2}-\frac{2 A}{m}-\frac{1}{m^{3}} \\ & =\left(A+B-(m+1) A^{2}\right)+\left(A-\frac{1}{m}\right)^{2} \geq 0 \end{aligned} $$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\frac{m+1}{m^{3}}$ and the right side is $\frac{m}{m^{4}}=\frac{1}{m^{3}}$. For the inductive step, suppose we have shown the result for $m+1$. Let $$ A=\sum_{k=m+1}^{n} \frac{1}{k^{2}} \quad \text { and } \quad B=\sum_{k=m+1}^{n} \frac{1}{k^{3}} $$ We know $A+B \geq(m+1) A^{2}$, and we want to show $$ \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right) \geq m\left(A+\frac{1}{m^{2}}\right)^{2} $$ Indeed, $$ \begin{aligned} \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right)-m\left(A+\frac{1}{m^{2}}\right)^{2} & =A+B+\frac{m+1}{m^{3}}-m A^{2}-\frac{2 A}{m}-\frac{1}{m^{3}} \\ & =\left(A+B-(m+1) A^{2}\right)+\left(A-\frac{1}{m}\right)^{2} \geq 0 \end{aligned} $$ and we are done.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
I Third approach by reducing $n \rightarrow \infty$, Michael Ren and Carl Schildkraut. First, we give: Claim (Reduction to $n \rightarrow \infty$ ) - If the problem is true when $n \rightarrow \infty$, it is true for all $n$. However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\left(\frac{1}{m^{2}}, \frac{1}{m^{3}}\right),\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}, \frac{1}{m^{3}}+\frac{1}{(m+1)^{3}}\right), \ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \rightarrow \infty$. Set $n=\infty$ henceforth. Let $$ A=\sum_{k=m}^{\infty} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{\infty} \frac{1}{k^{3}} $$ we want to show $B \geq m A^{2}-A$, which rearranges to $$ 1+4 m B \geq(2 m A-1)^{2} $$ Write $$ C=\sum_{k=m}^{\infty} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{\infty} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ Then $$ \frac{2}{2 k-1}-\frac{2}{2 k+1}=\frac{1}{k^{2}}+\frac{1}{k^{2}(2 k-1)(2 k+1)} $$ and $$ \frac{2}{(2 k-1)^{2}}-\frac{2}{(2 k+1)^{2}}=\frac{1}{k^{3}}+\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}, $$ so that $$ A=\frac{2}{2 m-1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-D $$ Our inequality we wish to show becomes $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ We in fact show two claims: Claim - We have $$ \frac{2 m+1 / 2}{2 m-1} C \geq D $$ $$ \frac{2 m+1 / 2}{2 m-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ for $k \geq m$. It suffices to show $$ \frac{2 k+1 / 2}{2 k-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ which is equivalent to $k(2 k+1 / 2)(2 k+1) \geq 8 k^{2}-1$. This holds for all $k \geq 1$. ## Claim - We have $$ \frac{1 / 2}{2 m-1} C \geq m C^{2} $$ $$ \frac{1}{2 m(2 m-1)}=\sum_{k=m}^{\infty}\left(\frac{1}{2 k(2 k-1)}-\frac{1}{2(k+1)(2 k+1)}\right)=\sum_{k=m}^{\infty} \frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)} $$ comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \geq 2(k+1)$ for $k \geq 1$ gives the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
I Third approach by reducing $n \rightarrow \infty$, Michael Ren and Carl Schildkraut. First, we give: Claim (Reduction to $n \rightarrow \infty$ ) - If the problem is true when $n \rightarrow \infty$, it is true for all $n$. However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\left(\frac{1}{m^{2}}, \frac{1}{m^{3}}\right),\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}, \frac{1}{m^{3}}+\frac{1}{(m+1)^{3}}\right), \ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \rightarrow \infty$. Set $n=\infty$ henceforth. Let $$ A=\sum_{k=m}^{\infty} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{\infty} \frac{1}{k^{3}} $$ we want to show $B \geq m A^{2}-A$, which rearranges to $$ 1+4 m B \geq(2 m A-1)^{2} $$ Write $$ C=\sum_{k=m}^{\infty} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{\infty} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ Then $$ \frac{2}{2 k-1}-\frac{2}{2 k+1}=\frac{1}{k^{2}}+\frac{1}{k^{2}(2 k-1)(2 k+1)} $$ and $$ \frac{2}{(2 k-1)^{2}}-\frac{2}{(2 k+1)^{2}}=\frac{1}{k^{3}}+\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}, $$ so that $$ A=\frac{2}{2 m-1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-D $$ Our inequality we wish to show becomes $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ We in fact show two claims: Claim - We have $$ \frac{2 m+1 / 2}{2 m-1} C \geq D $$ $$ \frac{2 m+1 / 2}{2 m-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ for $k \geq m$. It suffices to show $$ \frac{2 k+1 / 2}{2 k-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ which is equivalent to $k(2 k+1 / 2)(2 k+1) \geq 8 k^{2}-1$. This holds for all $k \geq 1$. ## Claim - We have $$ \frac{1 / 2}{2 m-1} C \geq m C^{2} $$ $$ \frac{1}{2 m(2 m-1)}=\sum_{k=m}^{\infty}\left(\frac{1}{2 k(2 k-1)}-\frac{1}{2(k+1)(2 k+1)}\right)=\sum_{k=m}^{\infty} \frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)} $$ comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \geq 2(k+1)$ for $k \geq 1$ gives the desired result.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \rightarrow \infty$ reduction. Similarly to before, define $$ A=\sum_{k=m}^{n} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{n} \frac{1}{k^{3}} $$ we want to show $1+4 m B \geq(2 m A-1)^{2}$. Writing $$ C=\sum_{k=m}^{n} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{n} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ We compute $$ A=\frac{2}{2 m-1}-\frac{2}{2 n+1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-\frac{2}{(2 n+1)^{2}}-D . $$ Then, the inequality we wish to show reduces (as in the previous solution) to $$ \frac{2 m+1}{2 m-1} C+\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq D+m C^{2}+\frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ We deal first with the terms not containing the variable $n$, i.e. we show that $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ For this part, the two claims from the previous solution go through exactly as written above, and we have $C \leq 1 /(2 m(2 m-1))$. We now need to show $$ \frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq \frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ (this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving $$ \frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \geq \frac{2}{(2 m-1)(2 n+1)} $$ Expanding and writing in terms of $n$, this is equivalent to $$ n \geq \frac{1+2(m-1)(2 m+1)}{4 m}=m-\frac{2 m+1}{4 m} $$ which holds for all $n \geq m$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \rightarrow \infty$ reduction. Similarly to before, define $$ A=\sum_{k=m}^{n} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{n} \frac{1}{k^{3}} $$ we want to show $1+4 m B \geq(2 m A-1)^{2}$. Writing $$ C=\sum_{k=m}^{n} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{n} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ We compute $$ A=\frac{2}{2 m-1}-\frac{2}{2 n+1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-\frac{2}{(2 n+1)^{2}}-D . $$ Then, the inequality we wish to show reduces (as in the previous solution) to $$ \frac{2 m+1}{2 m-1} C+\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq D+m C^{2}+\frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ We deal first with the terms not containing the variable $n$, i.e. we show that $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ For this part, the two claims from the previous solution go through exactly as written above, and we have $C \leq 1 /(2 m(2 m-1))$. We now need to show $$ \frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq \frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ (this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving $$ \frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \geq \frac{2}{(2 m-1)(2 n+1)} $$ Expanding and writing in terms of $n$, this is equivalent to $$ n \geq \frac{1+2(m-1)(2 m+1)}{4 m}=m-\frac{2 m+1}{4 m} $$ which holds for all $n \geq m$.
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Find all positive integers $n$ for which it is possible to color some cells of an infinite grid of unit squares red, such that each rectangle consisting of exactly $n$ cells (and whose edges lie along the lines of the grid) contains an odd number of red cells.
|
We claim that this is possible for all positive integers $n$. Call a positive integer for which such a coloring is possible good. To show that all positive integers $n$ are good we prove the following: (i) If $n$ is good and $p$ is an odd prime, then $p n$ is good; (ii) For every $k \geq 0$, the number $n=2^{k}$ is good. Together, (i) and (ii) imply that all positive integers are good. Thus every coloring that works for $n$ automatically also works for $p n$. Claim - For each of these $k+1$ shapes, there exists a coloring with two properties: - Every rectangle with $n$ cells and shape $2^{m} \times 2^{k-m}$ contains an odd number of red cells. - Every rectangle with $n$ cells and a different shape contains an even number of red cells.  A $2^{m} \times 2^{k-m}$ rectangle contains every possible pair $\left(x \bmod 2^{m}, y \bmod 2^{k-m}\right)$ exactly once, so such a rectangle will contain one red cell (an odd number). On the other hand, consider a $2^{\ell} \times 2^{k-\ell}$ rectangle with $\ell>m$. The set of cells this covers is $(x, y)$ where $x$ covers a range of size $2^{\ell}$ and $y$ covers a range of size $2^{k-\ell}$. The number of red cells is the count of $x$ with $x \equiv 0 \bmod 2^{m}$ multiplied by the count of $y$ with $y \equiv 0 \bmod 2^{k-m}$. The former number is exactly $2^{\ell-k}$ because $2^{k}$ divides $2^{\ell}$ (while the latter is 0 or 1) so the number of red cells is even. The $\ell<m$ case is similar. Finally, given these $k+1$ colorings, we can add them up modulo 2, i.e. a cell will be colored red if it is red in an odd number of these $k+1$ coloring. We illustrate $n=4$ as an example; the coloring is 4 -periodic in both axes so we only show one $4 \times 4$ cell.  This solves the problem. Remark. The final coloring can be described as follows: color $(x, y)$ red if $$ \max \left(0, \min \left(\nu_{2}(x), k\right)+\min \left(\nu_{2}(y), k\right)-k+1\right) $$ is odd. Remark (Luke Robitaille). Alternatively for (i), if $n=2^{e} k$ for odd $k$ then one may dissect an $a \times b$ rectangle with area $n$ into $k$ rectangles of area $2^{e}$, each $2^{\nu_{2}(a)} \times 2^{\nu_{2}(b)}$. This gives a way to deduce the problem from (ii) without having to consider odd prime numbers. $$ f(x, y)=\sum_{i=0}^{2^{k}-1} \sum_{j=0}^{2^{k}-1} \lambda_{i, j} x^{i} y^{j} $$ denote its generating function, where $f \in \mathbb{F}_{2}[x, y]$. For this to be valid, we need that for any $2^{p} \times 2^{q}$ rectangle with area $n$, the sum of the coefficients of $f$ over it should be one, modulo $x^{2^{k}}=y^{2^{k}}=1$. In other words, whenever $p+q=k$, we must have $$ f(x, y)\left(1+\cdots+x^{2^{p}-1}\right)\left(1+\cdots+y^{2^{q}-1}\right)=\left(1+\cdots+x^{2^{k}-1}\right)\left(1+\cdots+y^{2^{k}-1}\right) $$ taken modulo $x^{2^{k}}=y^{2^{k}}=1$. The idea is to rewrite these expressions: because we're in characteristic 2, the given assertion is $(x+1)^{2^{k}}=(y+1)^{2^{k}}=0$, and the requested property is $$ f(x, y)(x+1)^{2^{p}-1}(y+1)^{2^{q}-1}=(x+1)^{2^{k}-1}(y+1)^{2^{k}-1} . $$ This suggests the substitution $g(x, y)=f(x+1, y+1)$ : then we can replace $(x+1, y+1) \mapsto$ $(x, y)$ to simplify the requested property significantly: Whenever $p+q=k$, we must have $$ g(x, y) x^{2^{p}-1} y^{2^{q}-1}=x^{2^{k}-1} y^{2^{k}-1} $$ modulo $x^{2^{k}}$ and $y^{2^{k}}$. However, now the construction of $g$ is very simple: for example, the choice $$ g(x, y)=\sum_{p+q=k} x^{2^{k}-2^{p}} y^{2^{k}-2^{q}} $$ works. The end. Remark. Unraveling the substitutions seen here, it's possible to show that this is actually the same construction provided in the first solution.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find all positive integers $n$ for which it is possible to color some cells of an infinite grid of unit squares red, such that each rectangle consisting of exactly $n$ cells (and whose edges lie along the lines of the grid) contains an odd number of red cells.
|
We claim that this is possible for all positive integers $n$. Call a positive integer for which such a coloring is possible good. To show that all positive integers $n$ are good we prove the following: (i) If $n$ is good and $p$ is an odd prime, then $p n$ is good; (ii) For every $k \geq 0$, the number $n=2^{k}$ is good. Together, (i) and (ii) imply that all positive integers are good. Thus every coloring that works for $n$ automatically also works for $p n$. Claim - For each of these $k+1$ shapes, there exists a coloring with two properties: - Every rectangle with $n$ cells and shape $2^{m} \times 2^{k-m}$ contains an odd number of red cells. - Every rectangle with $n$ cells and a different shape contains an even number of red cells.  A $2^{m} \times 2^{k-m}$ rectangle contains every possible pair $\left(x \bmod 2^{m}, y \bmod 2^{k-m}\right)$ exactly once, so such a rectangle will contain one red cell (an odd number). On the other hand, consider a $2^{\ell} \times 2^{k-\ell}$ rectangle with $\ell>m$. The set of cells this covers is $(x, y)$ where $x$ covers a range of size $2^{\ell}$ and $y$ covers a range of size $2^{k-\ell}$. The number of red cells is the count of $x$ with $x \equiv 0 \bmod 2^{m}$ multiplied by the count of $y$ with $y \equiv 0 \bmod 2^{k-m}$. The former number is exactly $2^{\ell-k}$ because $2^{k}$ divides $2^{\ell}$ (while the latter is 0 or 1) so the number of red cells is even. The $\ell<m$ case is similar. Finally, given these $k+1$ colorings, we can add them up modulo 2, i.e. a cell will be colored red if it is red in an odd number of these $k+1$ coloring. We illustrate $n=4$ as an example; the coloring is 4 -periodic in both axes so we only show one $4 \times 4$ cell.  This solves the problem. Remark. The final coloring can be described as follows: color $(x, y)$ red if $$ \max \left(0, \min \left(\nu_{2}(x), k\right)+\min \left(\nu_{2}(y), k\right)-k+1\right) $$ is odd. Remark (Luke Robitaille). Alternatively for (i), if $n=2^{e} k$ for odd $k$ then one may dissect an $a \times b$ rectangle with area $n$ into $k$ rectangles of area $2^{e}$, each $2^{\nu_{2}(a)} \times 2^{\nu_{2}(b)}$. This gives a way to deduce the problem from (ii) without having to consider odd prime numbers. $$ f(x, y)=\sum_{i=0}^{2^{k}-1} \sum_{j=0}^{2^{k}-1} \lambda_{i, j} x^{i} y^{j} $$ denote its generating function, where $f \in \mathbb{F}_{2}[x, y]$. For this to be valid, we need that for any $2^{p} \times 2^{q}$ rectangle with area $n$, the sum of the coefficients of $f$ over it should be one, modulo $x^{2^{k}}=y^{2^{k}}=1$. In other words, whenever $p+q=k$, we must have $$ f(x, y)\left(1+\cdots+x^{2^{p}-1}\right)\left(1+\cdots+y^{2^{q}-1}\right)=\left(1+\cdots+x^{2^{k}-1}\right)\left(1+\cdots+y^{2^{k}-1}\right) $$ taken modulo $x^{2^{k}}=y^{2^{k}}=1$. The idea is to rewrite these expressions: because we're in characteristic 2, the given assertion is $(x+1)^{2^{k}}=(y+1)^{2^{k}}=0$, and the requested property is $$ f(x, y)(x+1)^{2^{p}-1}(y+1)^{2^{q}-1}=(x+1)^{2^{k}-1}(y+1)^{2^{k}-1} . $$ This suggests the substitution $g(x, y)=f(x+1, y+1)$ : then we can replace $(x+1, y+1) \mapsto$ $(x, y)$ to simplify the requested property significantly: Whenever $p+q=k$, we must have $$ g(x, y) x^{2^{p}-1} y^{2^{q}-1}=x^{2^{k}-1} y^{2^{k}-1} $$ modulo $x^{2^{k}}$ and $y^{2^{k}}$. However, now the construction of $g$ is very simple: for example, the choice $$ g(x, y)=\sum_{p+q=k} x^{2^{k}-2^{p}} y^{2^{k}-2^{q}} $$ works. The end. Remark. Unraveling the substitutions seen here, it's possible to show that this is actually the same construction provided in the first solution.
|
{
"exam": "USA_TSTST",
"problem_label": "3",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $n \geq 3$ be an integer and let $K_{n}$ be the complete graph on $n$ vertices. Each edge of $K_{n}$ is colored either red, green, or blue. Let $A$ denote the number of triangles in $K_{n}$ with all edges of the same color, and let $B$ denote the number of triangles in $K_{n}$ with all edges of different colors. Prove that $$ B \leq 2 A+\frac{n(n-1)}{3} . $$
|
$ Consider all unordered pairs of different edges which share exactly one vertex (call these vees for convenience). Assign each vee a charge of +2 if its edge colors are the same, and a charge of -1 otherwise. We compute the total charge in two ways. ## 【 Total charge by summing over triangles. Note that - each monochromatic triangle has a charge of +6 , - each bichromatic triangle has a charge of 0 , and - each trichromatic triangle has a charge of -3 . Since each vee contributes to exactly one triangle, we obtain that the total charge is $6 A-3 B$. 【 Total charge by summing over vertices. We can also calculate the total charge by examining the centers of the vees. If a vertex has $a$ red edges, $b$ green edges, and $c$ blue edges, the vees centered at that vertex contribute a total charge of $$ \begin{aligned} & 2\left[\binom{a}{2}+\binom{b}{2}+\binom{c}{2}\right]-(a b+a c+b c) \\ = & \left(a^{2}-a+b^{2}-b+c^{2}-c\right)-(a b+a c+b c) \\ = & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(a+b+c) \\ = & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(n-1) \\ \geq & -(n-1) . \end{aligned} $$ In particular, the total charge is at least $-n(n-1)$. đ Conclusion. Thus, we obtain $$ 6 A-3 B \geq-n(n-1) \Longleftrightarrow B \leq 2 A+\frac{n(n-1)}{3} $$ as desired.
|
B \leq 2 A+\frac{n(n-1)}{3}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 3$ be an integer and let $K_{n}$ be the complete graph on $n$ vertices. Each edge of $K_{n}$ is colored either red, green, or blue. Let $A$ denote the number of triangles in $K_{n}$ with all edges of the same color, and let $B$ denote the number of triangles in $K_{n}$ with all edges of different colors. Prove that $$ B \leq 2 A+\frac{n(n-1)}{3} . $$
|
$ Consider all unordered pairs of different edges which share exactly one vertex (call these vees for convenience). Assign each vee a charge of +2 if its edge colors are the same, and a charge of -1 otherwise. We compute the total charge in two ways. ## 【 Total charge by summing over triangles. Note that - each monochromatic triangle has a charge of +6 , - each bichromatic triangle has a charge of 0 , and - each trichromatic triangle has a charge of -3 . Since each vee contributes to exactly one triangle, we obtain that the total charge is $6 A-3 B$. 【 Total charge by summing over vertices. We can also calculate the total charge by examining the centers of the vees. If a vertex has $a$ red edges, $b$ green edges, and $c$ blue edges, the vees centered at that vertex contribute a total charge of $$ \begin{aligned} & 2\left[\binom{a}{2}+\binom{b}{2}+\binom{c}{2}\right]-(a b+a c+b c) \\ = & \left(a^{2}-a+b^{2}-b+c^{2}-c\right)-(a b+a c+b c) \\ = & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(a+b+c) \\ = & \left(a^{2}+b^{2}+c^{2}-a b-a c-b c\right)-(n-1) \\ \geq & -(n-1) . \end{aligned} $$ In particular, the total charge is at least $-n(n-1)$. đ Conclusion. Thus, we obtain $$ 6 A-3 B \geq-n(n-1) \Longleftrightarrow B \leq 2 A+\frac{n(n-1)}{3} $$ as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "4",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. ## 【T First solution. $$ \begin{aligned} p+3 & =3+\sum_{\text {cyc }}\left(\frac{x}{y}+\frac{y}{x}\right)=3+\frac{x^{2}(y+z)+y^{2}(z+x)+z^{2}(x+y)}{x y z} \\ & =\frac{(x+y+z)(x y+y z+z x)}{x y z} \\ q-3 & =-3+\sum_{\text {cyc }} \frac{y^{2}}{z x}=\frac{x^{3}+y^{3}+z^{3}-3 x y z}{x y z} \\ & =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)}{x y z} . \end{aligned} $$ It follows that $$ \begin{aligned} \mathbb{R} & \ni 3(p+3)+(q-3) \\ & =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}+2(x y+y z+z x)\right)}{x y z} \\ & =\frac{(x+y+z)^{3}}{x y z} \end{aligned} $$ Now, note that if $x+y+z=0$, then $p=-3, q=3$ so we are done. Scale $x, y, z$ in such a way that $x+y+z$ is nonzero and real; hence so is $x y z$. Thus, as $p+3 \in \mathbb{R}$, we conclude $x y+y z+z x \in \mathbb{R}$ as well. Hence, $x, y, z$ are the roots of a cubic with real coefficients. Thus, - either all three of $\{x, y, z\}$ are real (which implies $a, b, c \in \mathbb{R}$ ), - or two of $\{x, y, z\}$ are a complex conjugate pair (which implies one of $a, b, c$ has absolute value 1). Both of these were forbidden by hypothesis. Construction As we saw in the setup, $(p, q)=(-3,3)$ will occur as long as $x+y+z=0$, and no two of $x, y, z$ to share the same magnitude or are collinear with the origin. This is easy to do; for example, we could choose $(x, y, z)=(3,4 i,-(3+4 i))$. Hence $a=\frac{3}{4 i}$, $b=-\frac{4 i}{3+4 i}, c=-\frac{3+4 i}{3}$ satisfies the hypotheses of the problem statement.
|
(-3,3)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. ## 【T First solution. $$ \begin{aligned} p+3 & =3+\sum_{\text {cyc }}\left(\frac{x}{y}+\frac{y}{x}\right)=3+\frac{x^{2}(y+z)+y^{2}(z+x)+z^{2}(x+y)}{x y z} \\ & =\frac{(x+y+z)(x y+y z+z x)}{x y z} \\ q-3 & =-3+\sum_{\text {cyc }} \frac{y^{2}}{z x}=\frac{x^{3}+y^{3}+z^{3}-3 x y z}{x y z} \\ & =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)}{x y z} . \end{aligned} $$ It follows that $$ \begin{aligned} \mathbb{R} & \ni 3(p+3)+(q-3) \\ & =\frac{(x+y+z)\left(x^{2}+y^{2}+z^{2}+2(x y+y z+z x)\right)}{x y z} \\ & =\frac{(x+y+z)^{3}}{x y z} \end{aligned} $$ Now, note that if $x+y+z=0$, then $p=-3, q=3$ so we are done. Scale $x, y, z$ in such a way that $x+y+z$ is nonzero and real; hence so is $x y z$. Thus, as $p+3 \in \mathbb{R}$, we conclude $x y+y z+z x \in \mathbb{R}$ as well. Hence, $x, y, z$ are the roots of a cubic with real coefficients. Thus, - either all three of $\{x, y, z\}$ are real (which implies $a, b, c \in \mathbb{R}$ ), - or two of $\{x, y, z\}$ are a complex conjugate pair (which implies one of $a, b, c$ has absolute value 1). Both of these were forbidden by hypothesis. Construction As we saw in the setup, $(p, q)=(-3,3)$ will occur as long as $x+y+z=0$, and no two of $x, y, z$ to share the same magnitude or are collinear with the origin. This is easy to do; for example, we could choose $(x, y, z)=(3,4 i,-(3+4 i))$. Hence $a=\frac{3}{4 i}$, $b=-\frac{4 i}{3+4 i}, c=-\frac{3+4 i}{3}$ satisfies the hypotheses of the problem statement.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. I Second solution, found by contestants. The main idea is to make the substitution $$ x=a+\frac{1}{c}, \quad y=b+\frac{1}{a}, \quad z=c+\frac{1}{b} . $$ Then we can check that $$ \begin{aligned} x+y+z & =p \\ x y+y z+z x & =p+q+3 \\ x y z & =p+2 . \end{aligned} $$ Therefore $x, y, z$ are the roots of a cubic with real coefficients. As in the previous solution, we note that this cubic must either have all real roots, or a complex conjugate pair of roots. We also have the relation $a(y+1)=a b+a+1=x+1$, and likewise $b(z+1)=y+1, c(x+1)=z+1$. This means that if any of $x, y, z$ are equal to -1, then all are equal to -1 . Assume for the sake of contradiction that none are equal to -1 . In the case where the cubic has three real roots, $a=\frac{x+1}{y+1}$ would be real. On the other hand, if there is a complex conjugate pair (without loss of generality, $x$ and $y$ ) then $a$ has magnitude 1. Therefore this cannot occur. We conclude that $x=y=z=-1$, so $p=-3$ and $q=3$. The solutions $(a, b, c)$ can then be parameterized as $\left(a,-1-\frac{1}{a},-\frac{1}{1+a}\right)$. To construct a solution, we need to choose a specific value of $a$ such that none of the wrong conditions hold; when $a=2 i$, say, we obtain the solution $\left(2 i,-1+\frac{i}{2}, \frac{-1+2 i}{5}\right)$.
|
(-3, 3)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. I Second solution, found by contestants. The main idea is to make the substitution $$ x=a+\frac{1}{c}, \quad y=b+\frac{1}{a}, \quad z=c+\frac{1}{b} . $$ Then we can check that $$ \begin{aligned} x+y+z & =p \\ x y+y z+z x & =p+q+3 \\ x y z & =p+2 . \end{aligned} $$ Therefore $x, y, z$ are the roots of a cubic with real coefficients. As in the previous solution, we note that this cubic must either have all real roots, or a complex conjugate pair of roots. We also have the relation $a(y+1)=a b+a+1=x+1$, and likewise $b(z+1)=y+1, c(x+1)=z+1$. This means that if any of $x, y, z$ are equal to -1, then all are equal to -1 . Assume for the sake of contradiction that none are equal to -1 . In the case where the cubic has three real roots, $a=\frac{x+1}{y+1}$ would be real. On the other hand, if there is a complex conjugate pair (without loss of generality, $x$ and $y$ ) then $a$ has magnitude 1. Therefore this cannot occur. We conclude that $x=y=z=-1$, so $p=-3$ and $q=3$. The solutions $(a, b, c)$ can then be parameterized as $\left(a,-1-\frac{1}{a},-\frac{1}{1+a}\right)$. To construct a solution, we need to choose a specific value of $a$ such that none of the wrong conditions hold; when $a=2 i$, say, we obtain the solution $\left(2 i,-1+\frac{i}{2}, \frac{-1+2 i}{5}\right)$.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. 【 Third solution by Luke Robitaille and Daniel Zhu. The answer is $p=-3$ and $q=3$. Let's first prove that no other $(p, q)$ work. Let $e_{1}=a+b+c$ and $e_{2}=a^{-1}+b^{-1}+c^{-1}=a b+a c+b c$. Also, let $f=e_{1} e_{2}$. Note that $p=e_{1}+e_{2}$. Our main insight is to consider the quantity $q^{\prime}=\frac{b}{a}+\frac{c}{b}+\frac{a}{c}$. Note that $f=q+q^{\prime}+3$. Also, $$ \begin{aligned} q q^{\prime} & =3+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}+\frac{b c}{a^{2}}+\frac{a c}{b^{2}}+\frac{a b}{c^{2}} \\ & =3+a^{3}+b^{3}+c^{3}+a^{-3}+b^{-3}+c^{-3} \\ & =9+a^{3}+b^{3}+c^{3}-3 a b c+a^{-3}+b^{-3}+c^{-3}-3 a^{-1} b^{-1} c^{-1} \\ & =9+e_{1}\left(e_{1}^{2}-3 e_{2}\right)+e_{2}\left(e_{2}^{2}-3 e_{1}\right) \\ & =9+e_{1}^{3}+e_{2}^{3}-6 e_{1} e_{2} \\ & =9+p\left(p^{2}-3 f\right)-6 f \\ & =p^{3}-(3 p+6) f+9 . \end{aligned} $$ As a result, the quadratic with roots $q$ and $q^{\prime}$ is $x^{2}-(f-3) x+\left(p^{3}-(3 p+6) f+9\right)$, which implies that $$ q^{2}-q f+3 q+p^{3}-(3 p+6) f+9=0 \Longleftrightarrow(3 p+q+6) f=p^{3}+q^{2}+3 q+9 $$ At this point, two miracles occur. The first is the following claim: Claim - $f$ is not real. - $e_{1}$ and $e_{2}$ are real. Then, $a, b$, and $c$ are the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$, and since every cubic with real coefficients has at least one real root, at least one of $a, b$, and $c$ is real, contradiction. - $e_{1}$ and $e_{2}$ are conjugates. Then, the polynomial $x^{3}-\bar{e}_{2} x^{2}+\bar{e}_{1} x-1$, which has roots $\bar{a}^{-1}, \bar{b}^{-1}$, and $\bar{c}^{-1}$, is the same as the polynomial with $a, b, c$ as roots. We conclude that the multiset $\{a, b, c\}$ is invariant under inversion about the unit circle, so one of $a, b$, and $c$ must lie on the unit circle. This is yet another contradiction. As a result, we know that $3 p+q+6=p^{3}+q^{2}+3 q+9=0$. The second miracle is that substituting $q=-3 p-6$ into $q^{2}+3 q+p^{3}+9=0$, we get $$ 0=p^{3}+9 p^{2}+27 p+27=(p+3)^{3} $$ so $p=-3$. Thus $q=3$. It remains to construct valid $a, b$, and $c$. To do this, let's pick some $e_{1}$, let $e_{2}=-3-e_{1}$, and let $a, b$, and $c$ be the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$. It is clear that this guarantees $p=-3$. By our above calculations, $q$ and $q^{\prime}$ are the roots of the quadratic $x^{2}-(f-3) x+(3 f-18)$, so one of $q$ and $q^{\prime}$ must be 3 ; by changing the order of $a, b$, and $c$ if needed, we can guarantee this to be $q$. It suffices to show that for some choice of $e_{1}$, none of $a, b$, or $c$ are real or lie on the unit circle. To do this, note that we can rewrite $x^{3}-e_{1} x^{2}+\left(-3-e_{1}\right) x-1=0$ as $$ e_{1}=\frac{x^{3}-3 x-1}{x^{2}+x} $$ so all we need is a value of $e_{1}$ that is not $\frac{x^{3}-3 x-1}{x^{2}+x}$ for any real $x$ or $x$ on the unit circle. One way to do this is to choose any nonreal $e_{1}$ with $\left|e_{1}\right|<1 / 2$. This clearly rules out any real $x$. Also, if $|x|=1$, by the triangle inequality $\left|x^{3}-3 x-1\right| \geq|3 x|-\left|x^{3}\right|-|1|=1$ and $\left|x^{2}+x\right| \leq 2$, so $\left|\frac{x^{3}-3 x-1}{x^{2}+x}\right| \geq \frac{1}{2}$.
|
p=-3, q=3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $a, b$, and $c$ are three complex numbers with product 1 . Assume that none of $a, b$, and $c$ are real or have absolute value 1 . Define $$ p=(a+b+c)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \quad \text { and } \quad q=\frac{a}{b}+\frac{b}{c}+\frac{c}{a} . $$ Given that both $p$ and $q$ are real numbers, find all possible values of the ordered pair $(p, q)$.
|
We show $(p, q)=(-3,3)$ is the only possible ordered pair. 【 Third solution by Luke Robitaille and Daniel Zhu. The answer is $p=-3$ and $q=3$. Let's first prove that no other $(p, q)$ work. Let $e_{1}=a+b+c$ and $e_{2}=a^{-1}+b^{-1}+c^{-1}=a b+a c+b c$. Also, let $f=e_{1} e_{2}$. Note that $p=e_{1}+e_{2}$. Our main insight is to consider the quantity $q^{\prime}=\frac{b}{a}+\frac{c}{b}+\frac{a}{c}$. Note that $f=q+q^{\prime}+3$. Also, $$ \begin{aligned} q q^{\prime} & =3+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}+\frac{b c}{a^{2}}+\frac{a c}{b^{2}}+\frac{a b}{c^{2}} \\ & =3+a^{3}+b^{3}+c^{3}+a^{-3}+b^{-3}+c^{-3} \\ & =9+a^{3}+b^{3}+c^{3}-3 a b c+a^{-3}+b^{-3}+c^{-3}-3 a^{-1} b^{-1} c^{-1} \\ & =9+e_{1}\left(e_{1}^{2}-3 e_{2}\right)+e_{2}\left(e_{2}^{2}-3 e_{1}\right) \\ & =9+e_{1}^{3}+e_{2}^{3}-6 e_{1} e_{2} \\ & =9+p\left(p^{2}-3 f\right)-6 f \\ & =p^{3}-(3 p+6) f+9 . \end{aligned} $$ As a result, the quadratic with roots $q$ and $q^{\prime}$ is $x^{2}-(f-3) x+\left(p^{3}-(3 p+6) f+9\right)$, which implies that $$ q^{2}-q f+3 q+p^{3}-(3 p+6) f+9=0 \Longleftrightarrow(3 p+q+6) f=p^{3}+q^{2}+3 q+9 $$ At this point, two miracles occur. The first is the following claim: Claim - $f$ is not real. - $e_{1}$ and $e_{2}$ are real. Then, $a, b$, and $c$ are the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$, and since every cubic with real coefficients has at least one real root, at least one of $a, b$, and $c$ is real, contradiction. - $e_{1}$ and $e_{2}$ are conjugates. Then, the polynomial $x^{3}-\bar{e}_{2} x^{2}+\bar{e}_{1} x-1$, which has roots $\bar{a}^{-1}, \bar{b}^{-1}$, and $\bar{c}^{-1}$, is the same as the polynomial with $a, b, c$ as roots. We conclude that the multiset $\{a, b, c\}$ is invariant under inversion about the unit circle, so one of $a, b$, and $c$ must lie on the unit circle. This is yet another contradiction. As a result, we know that $3 p+q+6=p^{3}+q^{2}+3 q+9=0$. The second miracle is that substituting $q=-3 p-6$ into $q^{2}+3 q+p^{3}+9=0$, we get $$ 0=p^{3}+9 p^{2}+27 p+27=(p+3)^{3} $$ so $p=-3$. Thus $q=3$. It remains to construct valid $a, b$, and $c$. To do this, let's pick some $e_{1}$, let $e_{2}=-3-e_{1}$, and let $a, b$, and $c$ be the roots of $x^{3}-e_{1} x^{2}+e_{2} x-1$. It is clear that this guarantees $p=-3$. By our above calculations, $q$ and $q^{\prime}$ are the roots of the quadratic $x^{2}-(f-3) x+(3 f-18)$, so one of $q$ and $q^{\prime}$ must be 3 ; by changing the order of $a, b$, and $c$ if needed, we can guarantee this to be $q$. It suffices to show that for some choice of $e_{1}$, none of $a, b$, or $c$ are real or lie on the unit circle. To do this, note that we can rewrite $x^{3}-e_{1} x^{2}+\left(-3-e_{1}\right) x-1=0$ as $$ e_{1}=\frac{x^{3}-3 x-1}{x^{2}+x} $$ so all we need is a value of $e_{1}$ that is not $\frac{x^{3}-3 x-1}{x^{2}+x}$ for any real $x$ or $x$ on the unit circle. One way to do this is to choose any nonreal $e_{1}$ with $\left|e_{1}\right|<1 / 2$. This clearly rules out any real $x$. Also, if $|x|=1$, by the triangle inequality $\left|x^{3}-3 x-1\right| \geq|3 x|-\left|x^{3}\right|-|1|=1$ and $\left|x^{2}+x\right| \leq 2$, so $\left|\frac{x^{3}-3 x-1}{x^{2}+x}\right| \geq \frac{1}{2}$.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\prime}$ using the following claim. Claim - There is a point $P^{\prime}$ for which $$ \measuredangle A P H+\measuredangle A P^{\prime} H=\measuredangle B P H+\measuredangle B P^{\prime} H=\measuredangle C P H+\measuredangle C P^{\prime} H=0 . $$ Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\overline{A H}, \overline{B H}$, and $\overline{C H}$ respectively. Additionally, let $Q^{\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ).  $$ \text { Claim }-A B C P^{\prime} \approx X Y Z Q^{\prime} $$ $$ \measuredangle Y X Z=\measuredangle Y P Z=\measuredangle(\overline{B H}, \overline{C H})=-\measuredangle B A C $$ and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally, $$ \measuredangle H Q^{\prime} X=-\measuredangle H X Q=-\measuredangle H X A=\measuredangle H P A=-\measuredangle H P^{\prime} A $$ and cyclic variants, so summing in pairs gives $\measuredangle Y Q^{\prime} Z=-\measuredangle B P^{\prime} C$ and cyclic variants; this implies the similarity. Claim - $Q^{\prime}$ lies on the Euler line of triangle $X Y Z$. To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas, $$ \begin{aligned} {\left[G_{1} H P\right]+\left[G_{1} H Q\right] } & =\frac{[A H P]+[B H P]+[C H P]}{3}+\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\ & =\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\ & =\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\ & =\left[Q G_{2} H\right] \\ & =0 \end{aligned} $$ where the last line follows from the last claim. Therefore $\overline{G_{1} H}$ bisects $\overline{P Q}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\prime}$ using the following claim. Claim - There is a point $P^{\prime}$ for which $$ \measuredangle A P H+\measuredangle A P^{\prime} H=\measuredangle B P H+\measuredangle B P^{\prime} H=\measuredangle C P H+\measuredangle C P^{\prime} H=0 . $$ Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\overline{A H}, \overline{B H}$, and $\overline{C H}$ respectively. Additionally, let $Q^{\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ).  $$ \text { Claim }-A B C P^{\prime} \approx X Y Z Q^{\prime} $$ $$ \measuredangle Y X Z=\measuredangle Y P Z=\measuredangle(\overline{B H}, \overline{C H})=-\measuredangle B A C $$ and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally, $$ \measuredangle H Q^{\prime} X=-\measuredangle H X Q=-\measuredangle H X A=\measuredangle H P A=-\measuredangle H P^{\prime} A $$ and cyclic variants, so summing in pairs gives $\measuredangle Y Q^{\prime} Z=-\measuredangle B P^{\prime} C$ and cyclic variants; this implies the similarity. Claim - $Q^{\prime}$ lies on the Euler line of triangle $X Y Z$. To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas, $$ \begin{aligned} {\left[G_{1} H P\right]+\left[G_{1} H Q\right] } & =\frac{[A H P]+[B H P]+[C H P]}{3}+\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\ & =\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\ & =\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\ & =\left[Q G_{2} H\right] \\ & =0 \end{aligned} $$ where the last line follows from the last claim. Therefore $\overline{G_{1} H}$ bisects $\overline{P Q}$, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively. The first step is to translate the given geometric conditions into a single usable equation: Claim - We have the equation $$ (p+q) \sum_{\mathrm{cyc}} a^{3}\left(b^{2}-c^{2}\right)=(\bar{p}+\bar{q}) a b c \sum_{\mathrm{cyc}}\left(b c\left(b^{2}-c^{2}\right)\right) $$ $$ \begin{aligned} & \frac{(p-a)(q-a)}{(h-a)^{2}}=\frac{(p-a)(q-a)}{(b+c)^{2}} \in \mathbb{R} \\ \Longrightarrow & \frac{(p-a)(q-a)}{(b+c)^{2}}=\frac{\left(\frac{(p-a)(q-a)}{(b+c)^{2}}\right)}{}=\frac{(a \bar{p}-1)(a \bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\ \Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \bar{p}-1)(a \bar{q}-1) \\ \Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) . \end{aligned} $$ Writing the symmetric conditions that $\overline{B H}$ and $\overline{C H}$ bisect $\angle P B Q$ and $\angle P C Q$ gives three equations: $$ \begin{aligned} & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) \\ & b^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(b^{4}-c^{2} a^{2}\right)=b^{3}(p+q)-b c^{2} a^{2}(\bar{p}+\bar{q}) \end{aligned} $$ $$ c^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(c^{4}-a^{2} b^{2}\right)=c^{3}(p+q)-c a^{2} b^{2}(\bar{p}+\bar{q}) $$ Now, sum $\left(b^{2}-c^{2}\right)$ times the first equation, $\left(c^{2}-a^{2}\right)$ times the second equation, and $\left(a^{2}-b^{2}\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since $$ \sum_{\mathrm{cyc}}\left(a^{4}-b^{2} c^{2}\right)\left(b^{2}-c^{2}\right)=\sum_{\mathrm{cyc}}\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\right) $$ This gives (1) as desired. We can then factor (1): Claim - The left-hand side of (1) factors as $$ -(p+q)(a-b)(b-c)(c-a)(a b+b c+c a) $$ while the right-hand side factors as $$ -(\bar{p}+\bar{q})(a-b)(b-c)(c-a)(a+b+c) $$ Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\left(a^{2}-c^{2}\right)+a^{3}\left(c^{2}-a^{2}\right)+c^{3}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$. Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\left(a^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)+a^{2}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\left(b^{2}-c^{2}\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$. Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain $$ (p+q)(a b+b c+c a)=(\bar{p}+\bar{q}) a b c(a+b+c) \Longrightarrow(p+q) \bar{h}=(\bar{p}+\bar{q}) h $$ This implies that $\frac{\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\overline{P Q}$ lies on line $\overline{O H}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively. The first step is to translate the given geometric conditions into a single usable equation: Claim - We have the equation $$ (p+q) \sum_{\mathrm{cyc}} a^{3}\left(b^{2}-c^{2}\right)=(\bar{p}+\bar{q}) a b c \sum_{\mathrm{cyc}}\left(b c\left(b^{2}-c^{2}\right)\right) $$ $$ \begin{aligned} & \frac{(p-a)(q-a)}{(h-a)^{2}}=\frac{(p-a)(q-a)}{(b+c)^{2}} \in \mathbb{R} \\ \Longrightarrow & \frac{(p-a)(q-a)}{(b+c)^{2}}=\frac{\left(\frac{(p-a)(q-a)}{(b+c)^{2}}\right)}{}=\frac{(a \bar{p}-1)(a \bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\ \Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \bar{p}-1)(a \bar{q}-1) \\ \Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) . \end{aligned} $$ Writing the symmetric conditions that $\overline{B H}$ and $\overline{C H}$ bisect $\angle P B Q$ and $\angle P C Q$ gives three equations: $$ \begin{aligned} & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) \\ & b^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(b^{4}-c^{2} a^{2}\right)=b^{3}(p+q)-b c^{2} a^{2}(\bar{p}+\bar{q}) \end{aligned} $$ $$ c^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(c^{4}-a^{2} b^{2}\right)=c^{3}(p+q)-c a^{2} b^{2}(\bar{p}+\bar{q}) $$ Now, sum $\left(b^{2}-c^{2}\right)$ times the first equation, $\left(c^{2}-a^{2}\right)$ times the second equation, and $\left(a^{2}-b^{2}\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since $$ \sum_{\mathrm{cyc}}\left(a^{4}-b^{2} c^{2}\right)\left(b^{2}-c^{2}\right)=\sum_{\mathrm{cyc}}\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\right) $$ This gives (1) as desired. We can then factor (1): Claim - The left-hand side of (1) factors as $$ -(p+q)(a-b)(b-c)(c-a)(a b+b c+c a) $$ while the right-hand side factors as $$ -(\bar{p}+\bar{q})(a-b)(b-c)(c-a)(a+b+c) $$ Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\left(a^{2}-c^{2}\right)+a^{3}\left(c^{2}-a^{2}\right)+c^{3}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$. Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\left(a^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)+a^{2}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\left(b^{2}-c^{2}\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$. Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain $$ (p+q)(a b+b c+c a)=(\bar{p}+\bar{q}) a b c(a+b+c) \Longrightarrow(p+q) \bar{h}=(\bar{p}+\bar{q}) h $$ This implies that $\frac{\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\overline{P Q}$ lies on line $\overline{O H}$.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\frac{(a-p)(a-q)}{(b-c)^{2}}, \frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain $$ \begin{aligned} & {\left[\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right] p q } \\ - & {\left[\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}\right](p+q) } \end{aligned} $$ $$ +\left[\frac{a^{2} X}{(b-c)^{2}}+\frac{b^{2} Y}{(c-a)^{2}}+\frac{c^{2} Z}{(a-b)^{2}}\right] $$ which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma. ## Lemma There exist real $X, Y, Z$ for which $$ \begin{aligned} & \frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}=0 \text { and } \\ & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}} \neq 0 . \end{aligned} $$ $$ \begin{aligned} & \frac{(b-a) Y}{(c-a)^{2}}+\frac{(c-a) Z}{(a-b)^{2}} \\ = & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}-a\left(\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right) \\ = & 0 \end{aligned} $$ We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\frac{(b-a)^{3}}{(c-a)^{3}}=-\frac{Z}{Y}$ is real. This means $\angle B A C=60^{\circ}$ or $120^{\circ}$. By symmetry, the same is true of $\angle C B A$ and $\angle A C B$. This is impossible because $A B C$ is scalene. With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\alpha$ and $\beta$, depending only on $a, b$, and $c$, such that $\alpha \neq 0$ and $\alpha(p+q)+\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\frac{(a-p)(a-q)}{(b-c)^{2}}, \frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain $$ \begin{aligned} & {\left[\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right] p q } \\ - & {\left[\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}\right](p+q) } \end{aligned} $$ $$ +\left[\frac{a^{2} X}{(b-c)^{2}}+\frac{b^{2} Y}{(c-a)^{2}}+\frac{c^{2} Z}{(a-b)^{2}}\right] $$ which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma. ## Lemma There exist real $X, Y, Z$ for which $$ \begin{aligned} & \frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}=0 \text { and } \\ & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}} \neq 0 . \end{aligned} $$ $$ \begin{aligned} & \frac{(b-a) Y}{(c-a)^{2}}+\frac{(c-a) Z}{(a-b)^{2}} \\ = & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}-a\left(\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right) \\ = & 0 \end{aligned} $$ We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\frac{(b-a)^{3}}{(c-a)^{3}}=-\frac{Z}{Y}$ is real. This means $\angle B A C=60^{\circ}$ or $120^{\circ}$. By symmetry, the same is true of $\angle C B A$ and $\angle A C B$. This is impossible because $A B C$ is scalene. With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\alpha$ and $\beta$, depending only on $a, b$, and $c$, such that $\alpha \neq 0$ and $\alpha(p+q)+\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up. In a move, Vera may flip over one of the coins in the row, subject to the following rules: - On the first move, Vera may flip over any of the 2023 coins. - On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.) Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$. Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times. The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all. 【 Construction. For $k=0,1, \ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.  It is easy to check this works, and there are 4044 flips, as desired.
|
4044
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up. In a move, Vera may flip over one of the coins in the row, subject to the following rules: - On the first move, Vera may flip over any of the 2023 coins. - On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.) Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$. Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times. The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all. 【 Construction. For $k=0,1, \ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.  It is easy to check this works, and there are 4044 flips, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 【 Synthetic approach (from author). We prove the converse of the problem first: Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}$, and $\overline{A_{1} B_{2}}$ are concurrent.  Hence the result follows by Brianchon's theorem. Now suppose $p \neq 1$. Let $\overline{B_{2}^{\prime} C_{1}^{\prime}}$ be the dilation of $\overline{B_{2} C_{1}}$ with ratio $\frac{1}{p}$ at center $A$, and define $C_{2}^{\prime}, A_{1}^{\prime}, A_{2}^{\prime}, B_{1}^{\prime}$ similarly. The following diagram showcases the situation $p<1$.  By the reasoning in the $p=1$ case, note that $\overline{B_{1}^{\prime} C_{2}^{\prime}}, \overline{C_{1}^{\prime} A_{2}^{\prime}}$, and $\overline{A_{1}^{\prime} B_{2}^{\prime}}$ are concurrent. However, $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}, \overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\prime} C_{2}^{\prime}, C A C_{1}^{\prime} A_{2}^{\prime}$, and $A B A_{1}^{\prime} B_{2}^{\prime}$, and these quadrilaterals do not share an interior point, a contradiction. Thus $p \geq 1$. Similarly, we can show $p \leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).
|
1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 【 Synthetic approach (from author). We prove the converse of the problem first: Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}$, and $\overline{A_{1} B_{2}}$ are concurrent.  Hence the result follows by Brianchon's theorem. Now suppose $p \neq 1$. Let $\overline{B_{2}^{\prime} C_{1}^{\prime}}$ be the dilation of $\overline{B_{2} C_{1}}$ with ratio $\frac{1}{p}$ at center $A$, and define $C_{2}^{\prime}, A_{1}^{\prime}, A_{2}^{\prime}, B_{1}^{\prime}$ similarly. The following diagram showcases the situation $p<1$.  By the reasoning in the $p=1$ case, note that $\overline{B_{1}^{\prime} C_{2}^{\prime}}, \overline{C_{1}^{\prime} A_{2}^{\prime}}$, and $\overline{A_{1}^{\prime} B_{2}^{\prime}}$ are concurrent. However, $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}, \overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\prime} C_{2}^{\prime}, C A C_{1}^{\prime} A_{2}^{\prime}$, and $A B A_{1}^{\prime} B_{2}^{\prime}$, and these quadrilaterals do not share an interior point, a contradiction. Thus $p \geq 1$. Similarly, we can show $p \leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 『 Barycentric solution (by Carl, Krit, Milan). We show that, if the common perimeter is 1 , then the lines concur. To do this, we use barycentric coordinates. Let $A=(1: 0: 0)$, $B=(0: 1: 0)$, and $C=(0: 0: 1)$. Let $A_{1}=\left(0: 1-a_{1}: a_{1}\right), A_{2}=\left(0: a_{2}: 1-a_{2}\right)$, $B_{1}=\left(b_{1}: 0: 1-b_{1}\right), B_{2}=\left(1-b_{2}: 0: b_{2}\right), C_{1}=\left(1-c_{1}: c_{1}: 0\right)$, and $C_{2}=\left(c_{2}: 1-c_{2}: 0\right)$. The line $B_{1} C_{2}$ is defined by the equation $$ \operatorname{det}\left[\begin{array}{ccc} x & y & z \\ b_{1} & 0 & 1-b_{1} \\ c_{2} & 1-c_{2} & 0 \end{array}\right]=0 \text {; } $$ i.e. $$ x\left(-\left(1-b_{1}\right)\left(1-c_{2}\right)\right)+y\left(\left(1-b_{1}\right) c_{2}\right)+z\left(b_{1}\left(1-c_{2}\right)\right)=0 . $$ Computing the equations for the other lines cyclically, we get that the lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ concur if and only if $$ \operatorname{det}\left[\begin{array}{ccc} -\left(1-b_{1}\right)\left(1-c_{2}\right) & \left(1-b_{1}\right) c_{2} & b_{1}\left(1-c_{2}\right) \\ c_{1}\left(1-a_{2}\right) & -\left(1-c_{1}\right)\left(1-a_{2}\right) & \left(1-c_{1}\right) a_{2} \\ \left(1-a_{1}\right) b_{2} & a_{1}\left(1-b_{2}\right) & -\left(1-a_{1}\right)\left(1-b_{2}\right) \end{array}\right]=0 . $$ Let this matrix be $M$. We also define the similar matrix $$ N=\left[\begin{array}{ccc} -\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\ c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\ \left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right) \end{array}\right] . $$ Geometrically, det $N=0$ if and only if $B_{2}^{\prime} C_{1}^{\prime}, C_{2}^{\prime} A_{1}^{\prime}$, and $A_{2}^{\prime} B_{1}^{\prime}$ concur, where for a point $P$ on a side of triangle $A B C, P^{\prime}$ denotes its reflection over that side's midpoint. Claim - We have $\operatorname{det} M=\operatorname{det} N$. We use the definition of the determinant as a sum over permutations. The even permutations give us the following three terms: $$ \begin{aligned} -\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right)\left(1-a_{2}\right)\left(1-a_{1}\right)\left(1-b_{2}\right) & =-\prod_{i=1}^{2}\left(\left(1-a_{i}\right)\left(1-b_{i}\right)\left(1-c_{i}\right)\right) \\ \left(1-a_{1}\right) b_{2}\left(1-b_{1}\right) c_{2}\left(1-c_{1}\right) a_{2} & =\left(\left(1-a_{1}\right)\left(1-b_{1}\right)\left(1-c_{1}\right)\right)\left(a_{2} b_{2} c_{2}\right) \\ c_{1}\left(1-a_{2}\right) a_{1}\left(1-b_{2}\right) b_{1}\left(1-c_{2}\right) & =\left(\left(1-a_{2}\right)\left(1-b_{2}\right)\left(1-c_{2}\right)\right)\left(a_{1} b_{1} c_{1}\right) . \end{aligned} $$ The first term is invariant under $\Psi$, while the second and third terms are swapped under $\Psi$. For the odd permutations, we have a contribution to the determinant of $$ \sum_{\mathrm{cyc}}\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right) a_{2} a_{1}\left(1-b_{2}\right) $$ each summand is invariant under $\Psi$. This finishes the proof of our claim. Now, it suffices to show that, if $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ each have perimeter 1, then $$ \operatorname{det}\left[\begin{array}{ccc} -\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\ c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\ \left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right) . \end{array}\right]=0 $$ Indeed, we have $A B_{2}=b_{2}$ and $A C_{1}=c_{1}$, so by the law of cosines, $$ 1-b_{2}-c_{1}=1-A B_{2}-A C_{1}=B_{2} C_{1}=\sqrt{b_{2}^{2}+c_{1}^{2}-b_{2} c_{1}} $$ This gives $$ \left(1-b_{2}-c_{1}\right)^{2}=b_{2}^{2}+c_{1}^{2}-b_{2} c_{1} \Longrightarrow 1-2 b_{2}-2 c_{1}+3 b_{2} c_{1}=0 $$ Similarly, $1-2 c_{2}-2 a_{1}+3 c_{2} a_{1}=0$ and $1-2 a_{2}-2 b_{1}+3 a_{2} b_{1}=0$. Now, $$ \begin{aligned} N\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] & =\left[\begin{array}{l} -\left(1-b_{2}\right)\left(1-c_{1}\right)+\left(1-b_{2}\right) c_{1}+b_{2}\left(1-c_{1}\right) \\ -\left(1-c_{2}\right)\left(1-a_{1}\right)+\left(1-c_{2}\right) a_{1}+c_{2}\left(1-a_{1}\right) \\ -\left(1-a_{2}\right)\left(1-b_{1}\right)+\left(1-a_{2}\right) b_{1}+a_{2}\left(1-b_{1}\right) \end{array}\right] \\ & =\left[\begin{array}{l} -1+2 b_{2}+2 c_{1}-3 b_{2} c_{1} \\ -1+2 c_{2}+2 a_{1}-3 c_{2} a_{1} \\ -1+2 a_{2}+2 b_{1}-2 a_{2} b_{1} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right] . \end{aligned} $$ So it follows $\operatorname{det} N=0$, as desired.
|
1
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 『 Barycentric solution (by Carl, Krit, Milan). We show that, if the common perimeter is 1 , then the lines concur. To do this, we use barycentric coordinates. Let $A=(1: 0: 0)$, $B=(0: 1: 0)$, and $C=(0: 0: 1)$. Let $A_{1}=\left(0: 1-a_{1}: a_{1}\right), A_{2}=\left(0: a_{2}: 1-a_{2}\right)$, $B_{1}=\left(b_{1}: 0: 1-b_{1}\right), B_{2}=\left(1-b_{2}: 0: b_{2}\right), C_{1}=\left(1-c_{1}: c_{1}: 0\right)$, and $C_{2}=\left(c_{2}: 1-c_{2}: 0\right)$. The line $B_{1} C_{2}$ is defined by the equation $$ \operatorname{det}\left[\begin{array}{ccc} x & y & z \\ b_{1} & 0 & 1-b_{1} \\ c_{2} & 1-c_{2} & 0 \end{array}\right]=0 \text {; } $$ i.e. $$ x\left(-\left(1-b_{1}\right)\left(1-c_{2}\right)\right)+y\left(\left(1-b_{1}\right) c_{2}\right)+z\left(b_{1}\left(1-c_{2}\right)\right)=0 . $$ Computing the equations for the other lines cyclically, we get that the lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ concur if and only if $$ \operatorname{det}\left[\begin{array}{ccc} -\left(1-b_{1}\right)\left(1-c_{2}\right) & \left(1-b_{1}\right) c_{2} & b_{1}\left(1-c_{2}\right) \\ c_{1}\left(1-a_{2}\right) & -\left(1-c_{1}\right)\left(1-a_{2}\right) & \left(1-c_{1}\right) a_{2} \\ \left(1-a_{1}\right) b_{2} & a_{1}\left(1-b_{2}\right) & -\left(1-a_{1}\right)\left(1-b_{2}\right) \end{array}\right]=0 . $$ Let this matrix be $M$. We also define the similar matrix $$ N=\left[\begin{array}{ccc} -\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\ c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\ \left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right) \end{array}\right] . $$ Geometrically, det $N=0$ if and only if $B_{2}^{\prime} C_{1}^{\prime}, C_{2}^{\prime} A_{1}^{\prime}$, and $A_{2}^{\prime} B_{1}^{\prime}$ concur, where for a point $P$ on a side of triangle $A B C, P^{\prime}$ denotes its reflection over that side's midpoint. Claim - We have $\operatorname{det} M=\operatorname{det} N$. We use the definition of the determinant as a sum over permutations. The even permutations give us the following three terms: $$ \begin{aligned} -\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right)\left(1-a_{2}\right)\left(1-a_{1}\right)\left(1-b_{2}\right) & =-\prod_{i=1}^{2}\left(\left(1-a_{i}\right)\left(1-b_{i}\right)\left(1-c_{i}\right)\right) \\ \left(1-a_{1}\right) b_{2}\left(1-b_{1}\right) c_{2}\left(1-c_{1}\right) a_{2} & =\left(\left(1-a_{1}\right)\left(1-b_{1}\right)\left(1-c_{1}\right)\right)\left(a_{2} b_{2} c_{2}\right) \\ c_{1}\left(1-a_{2}\right) a_{1}\left(1-b_{2}\right) b_{1}\left(1-c_{2}\right) & =\left(\left(1-a_{2}\right)\left(1-b_{2}\right)\left(1-c_{2}\right)\right)\left(a_{1} b_{1} c_{1}\right) . \end{aligned} $$ The first term is invariant under $\Psi$, while the second and third terms are swapped under $\Psi$. For the odd permutations, we have a contribution to the determinant of $$ \sum_{\mathrm{cyc}}\left(1-b_{1}\right)\left(1-c_{2}\right)\left(1-c_{1}\right) a_{2} a_{1}\left(1-b_{2}\right) $$ each summand is invariant under $\Psi$. This finishes the proof of our claim. Now, it suffices to show that, if $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ each have perimeter 1, then $$ \operatorname{det}\left[\begin{array}{ccc} -\left(1-b_{2}\right)\left(1-c_{1}\right) & \left(1-b_{2}\right) c_{1} & b_{2}\left(1-c_{1}\right) \\ c_{2}\left(1-a_{1}\right) & -\left(1-c_{2}\right)\left(1-a_{1}\right) & \left(1-c_{2}\right) a_{1} \\ \left(1-a_{2}\right) b_{1} & a_{2}\left(1-b_{1}\right) & -\left(1-a_{2}\right)\left(1-b_{1}\right) . \end{array}\right]=0 $$ Indeed, we have $A B_{2}=b_{2}$ and $A C_{1}=c_{1}$, so by the law of cosines, $$ 1-b_{2}-c_{1}=1-A B_{2}-A C_{1}=B_{2} C_{1}=\sqrt{b_{2}^{2}+c_{1}^{2}-b_{2} c_{1}} $$ This gives $$ \left(1-b_{2}-c_{1}\right)^{2}=b_{2}^{2}+c_{1}^{2}-b_{2} c_{1} \Longrightarrow 1-2 b_{2}-2 c_{1}+3 b_{2} c_{1}=0 $$ Similarly, $1-2 c_{2}-2 a_{1}+3 c_{2} a_{1}=0$ and $1-2 a_{2}-2 b_{1}+3 a_{2} b_{1}=0$. Now, $$ \begin{aligned} N\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] & =\left[\begin{array}{l} -\left(1-b_{2}\right)\left(1-c_{1}\right)+\left(1-b_{2}\right) c_{1}+b_{2}\left(1-c_{1}\right) \\ -\left(1-c_{2}\right)\left(1-a_{1}\right)+\left(1-c_{2}\right) a_{1}+c_{2}\left(1-a_{1}\right) \\ -\left(1-a_{2}\right)\left(1-b_{1}\right)+\left(1-a_{2}\right) b_{1}+a_{2}\left(1-b_{1}\right) \end{array}\right] \\ & =\left[\begin{array}{l} -1+2 b_{2}+2 c_{1}-3 b_{2} c_{1} \\ -1+2 c_{2}+2 a_{1}-3 c_{2} a_{1} \\ -1+2 a_{2}+2 b_{1}-2 a_{2} b_{1} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right] . \end{aligned} $$ So it follows $\operatorname{det} N=0$, as desired.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ 【 First solution by author. For convenience in what follows, set $d=\nu_{p}(a)$, let $a=p^{d} \cdot b$, and let a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be essential if it equals one of its iterated finite differences. The key claim is the following. Claim (Characterization of essential functions) - A function $f$ is essential if and only if $$ f(x)+f\left(x+p^{d}\right)+\cdots+f\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. ## Lemma Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \equiv 0 \quad(\bmod p) $$ for all $x$. $$ h(x)=\Delta^{p^{d}} g(x)=\sum_{k=0}^{p^{d}}(-1)^{k}\binom{p^{d}}{k} g\left(x+p^{d}-k\right) $$ However, it is known that $\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \leq k \leq p^{d}-1$, so $$ h(x) \equiv g\left(x+p^{d}\right)+(-1)^{p^{d}} g(x) \quad(\bmod p) . $$ Using this, we easily obtain $$ \begin{aligned} & h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \\ \equiv & \begin{cases}0 & p>2 \\ 2\left(g(x)+g\left(x+p^{d}\right)+\cdots+g\left(x+(b-1) p^{d}\right)\right) & p=2\end{cases} \\ \equiv & 0 \quad(\bmod p) \end{aligned} $$ as desired. ## Corollary Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{e p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. $$ h_{1}(x)=\frac{h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)}{p} . $$ Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$. This immediately settles this direction, since $f$ is in the image of $\Delta^{e p^{d}}$. We will show that $\Delta$ is injective on $\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\mathcal{S}$ with $\Delta f=\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\lambda$. However, then $$ \begin{aligned} & g(0)+g\left(p^{e}\right)+\cdots+g\left((b-1) p^{e}\right) \\ = & (f(0)+\lambda)+\left(f\left(p^{e}\right)+\lambda\right)+\cdots+\left(f\left((b-1) p^{e}\right)+\lambda\right) \\ = & b \lambda \end{aligned} $$ This should also be zero. Since $p \nmid b$, we obtain $\lambda=0$, as desired. Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of $$ \left(p^{e}\right)^{a-p^{d}}=p^{e\left(a-p^{\nu_{p}(a)}\right)}, $$ as promised.
|
p^{e\left(a-p^{\nu_{p}(a)}\right)}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ 【 First solution by author. For convenience in what follows, set $d=\nu_{p}(a)$, let $a=p^{d} \cdot b$, and let a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be essential if it equals one of its iterated finite differences. The key claim is the following. Claim (Characterization of essential functions) - A function $f$ is essential if and only if $$ f(x)+f\left(x+p^{d}\right)+\cdots+f\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. ## Lemma Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \equiv 0 \quad(\bmod p) $$ for all $x$. $$ h(x)=\Delta^{p^{d}} g(x)=\sum_{k=0}^{p^{d}}(-1)^{k}\binom{p^{d}}{k} g\left(x+p^{d}-k\right) $$ However, it is known that $\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \leq k \leq p^{d}-1$, so $$ h(x) \equiv g\left(x+p^{d}\right)+(-1)^{p^{d}} g(x) \quad(\bmod p) . $$ Using this, we easily obtain $$ \begin{aligned} & h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \\ \equiv & \begin{cases}0 & p>2 \\ 2\left(g(x)+g\left(x+p^{d}\right)+\cdots+g\left(x+(b-1) p^{d}\right)\right) & p=2\end{cases} \\ \equiv & 0 \quad(\bmod p) \end{aligned} $$ as desired. ## Corollary Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{e p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. $$ h_{1}(x)=\frac{h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)}{p} . $$ Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$. This immediately settles this direction, since $f$ is in the image of $\Delta^{e p^{d}}$. We will show that $\Delta$ is injective on $\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\mathcal{S}$ with $\Delta f=\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\lambda$. However, then $$ \begin{aligned} & g(0)+g\left(p^{e}\right)+\cdots+g\left((b-1) p^{e}\right) \\ = & (f(0)+\lambda)+\left(f\left(p^{e}\right)+\lambda\right)+\cdots+\left(f\left((b-1) p^{e}\right)+\lambda\right) \\ = & b \lambda \end{aligned} $$ This should also be zero. Since $p \nmid b$, we obtain $\lambda=0$, as desired. Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of $$ \left(p^{e}\right)^{a-p^{d}}=p^{e\left(a-p^{\nu_{p}(a)}\right)}, $$ as promised.
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ II Second solution by Daniel Zhu. There are two parts to the proof: solving the $e=1$ case, and using the $e=1$ result to solve the general problem by induction on $e$. These parts are independent of each other. The case $e=1 \quad$ Represent functions $f$ as elements $$ \alpha_{f}:=\sum_{k \in \mathbb{Z} / a \mathbb{Z}} f(-k) x^{k} \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right) $$ Then, since $\alpha_{\Delta f}=(x-1) \alpha_{f}$, we wish to find the number of $\alpha \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right)$ such that $(x-1)^{m} \alpha=\alpha$ for some $m$. Now, make the substitution $y=x-1$ and let $P(y)=(y+1)^{a}-1$; we want to find $\alpha \in \mathbb{F}_{p}[y] /(P(y))$ such that $y^{m} \alpha=\alpha$ for some $m$. If we write $P(y)=y^{d} Q(y)$ with $Q(0) \neq 0$, then by the Chinese Remainder Theorem we have the ring isomorphism $$ \mathbb{F}_{p}[y] /(P(y)) \cong \mathbb{F}_{p}[y] /\left(y^{d}\right) \times \mathbb{F}_{p}[y] /(Q(y)) $$ Note that $y$ is nilpotent in the first factor, while it is a unit in the second factor. So the $\alpha$ that work are exactly those that are zero in the first factor; thus there are $p^{a-d}$ such $\alpha$. We can calculate $d=p^{v_{p}(a)}$ (via, say, Lucas's Theorem), so we are done. The general problem The general idea is as follows: call a $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z} e$-good if $\Delta^{m} f=f$ for some $m$. Our result above allows us to count the 1-good functions. Then, if $e \geq 1$, every $(e+1)$-good function, when reduced $\bmod p^{e}$, yields an $e$-good function, so we count $(e+1)$-good functions by counting how many reduce to any given $e$-good function. Formally, we use induction on $e$, with the $e=1$ case being treated above. Suppose now we have solved the problem for a given $e \geq 1$, and we now wish to solve it for $e+1$. For any function $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, let $\bar{g}: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be its reduction $\bmod p^{e}$. For a given $e$-good $f$, let $n(f)$ be the number of $(e+1)$-good $g$ with $\bar{g}=f$. The following two claims now finish the problem: Claim - If $f$ is $e$-good, then $n(f)>0$. $$ g, \Delta^{m} g, \Delta^{2 m} g, \ldots $$ Since there are finitely many functions $\mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, there must exist $a<b$ such that $\Delta^{a m} g=\Delta^{b m} g$. We claim $\Delta^{a m} g$ is the desired $(e+1)$ good function. To see this, first note that since $\overline{\Delta^{k} g}=\Delta^{k} \bar{g}$, we must have $\overline{\Delta^{a m} g}=\Delta^{a m} f=f$. Moreover, $$ \Delta^{(b-a) m}\left(\Delta^{a m} g\right)=\Delta^{b m} g=\Delta^{a m} g $$ so $\Delta^{a m} g$ is $(e+1)$-good. Claim - If $f$ is $e$-good, and $n(f)>0$, then $n(f)$ is exactly the number of 1-good functions, i.e. $p^{a-p^{v_{p}(a)}}$. To show that this condition is sufficient, note that $\overline{g+p^{e} h}=\bar{g}=f$. Moreover, if $\Delta^{m} g=g$ and $\Delta^{m^{\prime}} h=h$, then $$ \Delta^{m m^{\prime}}\left(g+p^{e} h\right)=\Delta^{m m^{\prime}} g+p^{e} \Delta^{m m^{\prime}} h=g+p^{e} h . $$ To show that this condition is necessary, let $g_{1}$ be any $(e+1)$-good function such that $\bar{g}_{1}=f$. Then $g_{1}-g$ is also $(e+1)$-good, since if $\Delta^{m} g=g, \Delta^{m^{\prime}} g_{1}=g_{1}$, we have $$ \Delta^{m m^{\prime}}\left(g_{1}-g\right)=\Delta^{m m^{\prime}} g_{1}-\Delta^{m m^{\prime}} g=g_{1}-g . $$ On the other hand, we also know that $g_{1}-g$ is divisible by $p^{e}$. This means that it must be $p^{e} h$ for some function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p \mathbb{Z}$, and it is not hard to show that $g_{1}-g$ being $(e+1)$-good means that $h$ is 1 -good.
|
p^{e\left(a-p^{\nu_{p}(a)}\right)}
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ II Second solution by Daniel Zhu. There are two parts to the proof: solving the $e=1$ case, and using the $e=1$ result to solve the general problem by induction on $e$. These parts are independent of each other. The case $e=1 \quad$ Represent functions $f$ as elements $$ \alpha_{f}:=\sum_{k \in \mathbb{Z} / a \mathbb{Z}} f(-k) x^{k} \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right) $$ Then, since $\alpha_{\Delta f}=(x-1) \alpha_{f}$, we wish to find the number of $\alpha \in \mathbb{F}_{p}[x] /\left(x^{a}-1\right)$ such that $(x-1)^{m} \alpha=\alpha$ for some $m$. Now, make the substitution $y=x-1$ and let $P(y)=(y+1)^{a}-1$; we want to find $\alpha \in \mathbb{F}_{p}[y] /(P(y))$ such that $y^{m} \alpha=\alpha$ for some $m$. If we write $P(y)=y^{d} Q(y)$ with $Q(0) \neq 0$, then by the Chinese Remainder Theorem we have the ring isomorphism $$ \mathbb{F}_{p}[y] /(P(y)) \cong \mathbb{F}_{p}[y] /\left(y^{d}\right) \times \mathbb{F}_{p}[y] /(Q(y)) $$ Note that $y$ is nilpotent in the first factor, while it is a unit in the second factor. So the $\alpha$ that work are exactly those that are zero in the first factor; thus there are $p^{a-d}$ such $\alpha$. We can calculate $d=p^{v_{p}(a)}$ (via, say, Lucas's Theorem), so we are done. The general problem The general idea is as follows: call a $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z} e$-good if $\Delta^{m} f=f$ for some $m$. Our result above allows us to count the 1-good functions. Then, if $e \geq 1$, every $(e+1)$-good function, when reduced $\bmod p^{e}$, yields an $e$-good function, so we count $(e+1)$-good functions by counting how many reduce to any given $e$-good function. Formally, we use induction on $e$, with the $e=1$ case being treated above. Suppose now we have solved the problem for a given $e \geq 1$, and we now wish to solve it for $e+1$. For any function $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, let $\bar{g}: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be its reduction $\bmod p^{e}$. For a given $e$-good $f$, let $n(f)$ be the number of $(e+1)$-good $g$ with $\bar{g}=f$. The following two claims now finish the problem: Claim - If $f$ is $e$-good, then $n(f)>0$. $$ g, \Delta^{m} g, \Delta^{2 m} g, \ldots $$ Since there are finitely many functions $\mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e+1} \mathbb{Z}$, there must exist $a<b$ such that $\Delta^{a m} g=\Delta^{b m} g$. We claim $\Delta^{a m} g$ is the desired $(e+1)$ good function. To see this, first note that since $\overline{\Delta^{k} g}=\Delta^{k} \bar{g}$, we must have $\overline{\Delta^{a m} g}=\Delta^{a m} f=f$. Moreover, $$ \Delta^{(b-a) m}\left(\Delta^{a m} g\right)=\Delta^{b m} g=\Delta^{a m} g $$ so $\Delta^{a m} g$ is $(e+1)$-good. Claim - If $f$ is $e$-good, and $n(f)>0$, then $n(f)$ is exactly the number of 1-good functions, i.e. $p^{a-p^{v_{p}(a)}}$. To show that this condition is sufficient, note that $\overline{g+p^{e} h}=\bar{g}=f$. Moreover, if $\Delta^{m} g=g$ and $\Delta^{m^{\prime}} h=h$, then $$ \Delta^{m m^{\prime}}\left(g+p^{e} h\right)=\Delta^{m m^{\prime}} g+p^{e} \Delta^{m m^{\prime}} h=g+p^{e} h . $$ To show that this condition is necessary, let $g_{1}$ be any $(e+1)$-good function such that $\bar{g}_{1}=f$. Then $g_{1}-g$ is also $(e+1)$-good, since if $\Delta^{m} g=g, \Delta^{m^{\prime}} g_{1}=g_{1}$, we have $$ \Delta^{m m^{\prime}}\left(g_{1}-g\right)=\Delta^{m m^{\prime}} g_{1}-\Delta^{m m^{\prime}} g=g_{1}-g . $$ On the other hand, we also know that $g_{1}-g$ is divisible by $p^{e}$. This means that it must be $p^{e} h$ for some function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p \mathbb{Z}$, and it is not hard to show that $g_{1}-g$ being $(e+1)$-good means that $h$ is 1 -good.
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": null,
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"solution_match": null,
"tier": "T0",
"year": "2023"
}
|
For every ordered pair of integers \((i,j)\) , not necessarily positive, we wish to select a point \(P_{i,j}\) in the Cartesian plane whose coordinates lie inside the unit square defined by
\[i< x< i + 1,\qquad j< y< j + 1.\]
Find all real numbers \(c > 0\) for which it's possible to choose these points such that for all integers \(i\) and \(j\) , the (possibly concave or degenerate) quadrilateral \(P_{i,j}P_{i + 1,j}P_{i + 1,j + 1}P_{i,j + 1}\) has perimeter strictly less than \(c\) .
|
Answer. \(c\geq 4\)
Proof \(c< 4\) is not possible. Let \(n\) be an arbitrary positive integer. We take an \(n\times n\) subgrid of unit squares (i.e. \(P_{i,j}\) for \(1\leq i,j\leq n\) ), and compute a lower bound on the average of all possible quadrilaterals from this subgrid.
Consider the average length of the "top side" of all possible quadrilaterals in this grid. Note that this is equal to:
\[\frac{1}{(n - 1)^2}\sum_{i = 1}^{n - 1}\sum_{j = 1}^{n - 1}P_{i,j}P_{i + 1,j}\geq \frac{1}{(n - 1)^2}\sum_{j = 1}^{n - 1}P_{1,j}P_{n,j} > \frac{n - 2}{n - 1}.\]
We can apply this bound to all four sides of the quadrilateral (the left, right, bottom, and top sides) to find that the average perimeter of all possible quadrilaterals is greater than
\[\frac{4(n - 2)}{n - 1} = 4 - \frac{4}{n - 1}.\]
This means we can always find a quadrilateral whose perimeter is at least \(4 - \frac{4}{n - 1}\) . By taking sufficiently large \(n\) , this lower bound will exceed \(c\) .
Proof \(c = 4\) is possible. We'll place point \(P_{i,j}\) at the coordinates \((f(i),f(j))\) for some function \(f:\mathbb{Z}\to \mathbb{R}\) . The perimeter of \(P_{i,j}P_{i + 1,j}P_{i + 1,j + 1}P_{i,j + 1}\) is then
\[2\big(|f(i + 1) - f(i)| + |f(j + 1) - f(j)|\big).\]
Therefore we have a valid construction for \(c = 4\) if \(f\) satisfies \(n< f(n)< n + 1\) and \(|f(n + 1) - f(n)|< 1\) for all \(n\) . This is achieved by
\[f(n) = n + 0.5 + \left\{ \begin{array}{ll} - \sum_{i = 1}^{n}\frac{1}{10^{i}} & \mathrm{if~}n\geq 0,\\ \sum_{i = 1}^{-n}\frac{1}{10^{i}} & \mathrm{if~}n< 0. \end{array} \right.\]
Let's check the conditions. The sum is bounded by \(\sum_{i = 1}^{\infty}\frac{1}{10^{i}} = \frac{1}{9}\) in magnitude, so \(n< f(n)< n + 1\) . Furthermore, we can verify that
\[f(n + 1) - f(n) = 1 - \left\{ \begin{array}{ll}\frac{1}{10^{n + 1}} & \mathrm{if~}n\geq 0,\\ \frac{1}{10^{-n}} & \mathrm{if~}n< 0 \end{array} \right.< 1.\]
|
c \geq 4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For every ordered pair of integers \((i,j)\) , not necessarily positive, we wish to select a point \(P_{i,j}\) in the Cartesian plane whose coordinates lie inside the unit square defined by
\[i< x< i + 1,\qquad j< y< j + 1.\]
Find all real numbers \(c > 0\) for which it's possible to choose these points such that for all integers \(i\) and \(j\) , the (possibly concave or degenerate) quadrilateral \(P_{i,j}P_{i + 1,j}P_{i + 1,j + 1}P_{i,j + 1}\) has perimeter strictly less than \(c\) .
|
Answer. \(c\geq 4\)
Proof \(c< 4\) is not possible. Let \(n\) be an arbitrary positive integer. We take an \(n\times n\) subgrid of unit squares (i.e. \(P_{i,j}\) for \(1\leq i,j\leq n\) ), and compute a lower bound on the average of all possible quadrilaterals from this subgrid.
Consider the average length of the "top side" of all possible quadrilaterals in this grid. Note that this is equal to:
\[\frac{1}{(n - 1)^2}\sum_{i = 1}^{n - 1}\sum_{j = 1}^{n - 1}P_{i,j}P_{i + 1,j}\geq \frac{1}{(n - 1)^2}\sum_{j = 1}^{n - 1}P_{1,j}P_{n,j} > \frac{n - 2}{n - 1}.\]
We can apply this bound to all four sides of the quadrilateral (the left, right, bottom, and top sides) to find that the average perimeter of all possible quadrilaterals is greater than
\[\frac{4(n - 2)}{n - 1} = 4 - \frac{4}{n - 1}.\]
This means we can always find a quadrilateral whose perimeter is at least \(4 - \frac{4}{n - 1}\) . By taking sufficiently large \(n\) , this lower bound will exceed \(c\) .
Proof \(c = 4\) is possible. We'll place point \(P_{i,j}\) at the coordinates \((f(i),f(j))\) for some function \(f:\mathbb{Z}\to \mathbb{R}\) . The perimeter of \(P_{i,j}P_{i + 1,j}P_{i + 1,j + 1}P_{i,j + 1}\) is then
\[2\big(|f(i + 1) - f(i)| + |f(j + 1) - f(j)|\big).\]
Therefore we have a valid construction for \(c = 4\) if \(f\) satisfies \(n< f(n)< n + 1\) and \(|f(n + 1) - f(n)|< 1\) for all \(n\) . This is achieved by
\[f(n) = n + 0.5 + \left\{ \begin{array}{ll} - \sum_{i = 1}^{n}\frac{1}{10^{i}} & \mathrm{if~}n\geq 0,\\ \sum_{i = 1}^{-n}\frac{1}{10^{i}} & \mathrm{if~}n< 0. \end{array} \right.\]
Let's check the conditions. The sum is bounded by \(\sum_{i = 1}^{\infty}\frac{1}{10^{i}} = \frac{1}{9}\) in magnitude, so \(n< f(n)< n + 1\) . Furthermore, we can verify that
\[f(n + 1) - f(n) = 1 - \left\{ \begin{array}{ll}\frac{1}{10^{n + 1}} & \mathrm{if~}n\geq 0,\\ \frac{1}{10^{-n}} & \mathrm{if~}n< 0 \end{array} \right.< 1.\]
|
{
"exam": "USA_TSTST",
"problem_label": "1",
"problem_match": "1. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 1.1\\) TSTST 2024/1, proposed by Karthik Vedula \n",
"tier": "T0",
"year": "2024"
}
|
Let \(p\) be an odd prime number. Suppose \(P\) and \(Q\) are polynomials with integer coefficients such that \(P(0) = Q(0) = 1\) , there is no nonconstant polynomial dividing both \(P\) and \(Q\) , and
\[1 + \frac{x}{1 + \frac{2x}{1 + \frac{\cdots}{1 + (p - 1)x}}} = \frac{P(x)}{Q(x)}.\]
Show that all coefficients of \(P\) except for the constant coefficient are divisible by \(p\) , and all coefficients of \(Q\) are not divisible by \(p\) .
|
\(\P\) Solution 1. We first make some general observations about rational functions represented through continued fractions.
Claim — Let \(a_{1}, a_{2}, \ldots\) , be a sequence of nonzero integers. Define the sequence of polynomials \(P_{1}(x) = 1\) , \(P_{2}(x) = 1 + a_{1}x\) , and
\[P_{k + 1}(x) = P_{k}(x) + a_{k}x P_{k - 1}(x)\]
for \(k \geq 1\) . Then the following properties hold for all \(k \geq 0\) :
- \(P_{k}(0) = 1\) ,
- \(\gcd (P_{k + 1}, P_{k}) = 1\) , and
- \(\deg P_{k} = \lfloor k / 2 \rfloor\) .
\[1 + \frac{a_{k}x}{1 + \frac{a_{k - 1}x}{\ddots}} = \frac{P_{k + 1}(x)}{P_{k}(x)}.\] \[1 + \frac{\ddots}{1 + a_{1}x}\]
Proof. These all follow by induction.
With the setup of the claim, the polynomials \(P\) and \(Q\) in the problem are exactly \(P_{p}\) and \(P_{p}\) for the sequence \(a_{1} = p - 1\) , \(a_{2} = p - 2\) , ..., \(a_{p - 1} = 1\) . From here, we will define \(P\) and \(Q\) in terms of this recurrence and make two transformations on the \(a_{i}\) .
First, subtract \(p\) from each \(a_{i}\) so we now have \(a_{1} = - 1\) , \(a_{2} = - 2\) , ..., \(a_{p - 1} = -(p - 1)\) . The coefficients of \(P\) and \(Q\) only have changed by a multiple of \(p\) . The claim also shows that \(P(0) = Q(0) = 1\) , \(\gcd (P, Q) = 1\) , and the degrees of \(P\) and \(Q\) have not changed, i.e. no leading terms have been added or removed. Therefore it is equivalent to work with this sequence instead.
Similarly, we can multiply \(a_{i}\) by \(- 1\) to get \(a_{1} = 1\) , \(a_{2} = 2\) , ..., \(a_{p - 1} = p - 1\) . This is equivalent to replacing \(x\) with \(- x\) , so some coefficients of \(P\) and \(Q\) are negated by this. The key conditions still remain unchanged.
Remark. For rigor, it's important to prove the facts about continued fractions first rather than going straight to the coefficient replacement as the requirements imposed by the problem statement on \(P\) and \(Q\) are not always preserved modulo \(p\) .
At this point, we are ready to directly calculate the polynomials \(P_{n}\) .
Claim — For all \(n\) , we have
\[P_{n}(x) = \sum_{k\geq 0}\frac{n!}{2^{k}k!(n - 2k)!} x^{k}.\]
Here, we define \(\frac{n!}{(n - 2k)!} = n(n - 1)\ldots (n - 2k + 1)\) so the sum actually stops at \(k = \lfloor n / 2\rfloor\) .
Proof. We use induction. The base cases are clear, and
\[P_{n} + n x P_{n - 1} = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + n x\sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{(n - 1)!}{(n - 2k - 1)!} x^{k}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k - 1)!} x^{k + 1}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + \sum_{k\geq 1}\frac{1}{2^{k - 1}(k - 1)!}\frac{n!}{(n - 2k + 1)!} x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\left[\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} +\frac{1}{2^{k - 1}(k - 1)!}\frac{n!}{(n - 2k + 1)!}\right]x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k + 1)!}\left[(n - 2k + 1) + 2k\right]x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\frac{1}{2^{k}k!}\frac{(n + 1)!}{(n - 2k + 1)!} x^{k}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{(n + 1)!}{(n - 2k + 1)!} x^{k}\] \[\qquad = P_{n + 1}.\]
At this point we can directly check the coefficients of \(P\) and \(Q\) . We have
\[P(x) = P_{p}(x) = \sum_{k\geq 0}\frac{p!}{2^{k}k!(p - 2k)!} x^{k}.\]
For \(k = 0\) , we get a coefficient of 1. For \(k \geq 1\) , the denominator is not a multiple of \(p\) , so the remaining coefficients are multiples of \(p\) . Meanwhile, the coefficients for \(Q\) are \(\frac{(p - 1)!}{2^{k}k!(p - 1 - 2k)!}\) . None of these are divisible by \(p\) because \((p - 1)!\) is not divisible by \(p\) .
Remark. This problem was created from the identity
\[\frac{1}{1 - \frac{x}{1 - \frac{2x}{1 - \frac{3x}{1 - \cdots}}}}\]
You can use this to solve the problem. However, the proof of the identity as well as the details to convert this into the given problem are very lengthy so this is only left as a remark.
## Solution 2.
## Lemma
Define a series of polynomials \(A_{n}\) , \(B_{n}\) , \(C_{n}\) , \(D_{n}\) by letting \(A_{1} = 1\) , \(B_{1} = x\) , \(C_{1} = 1\) , and \(D_{1} = 0\) , and for \(n \geq 2\) ,
\[A_{n} = A_{n - 1} + B_{n - 1} B_{n} = nxA_{n - 1\] \[C_{n} = C_{n - 1} + D_{n - 1} D_{n} = nxC_{n - 1}.\]
Then, if we define \(f_{k}(t) = 1 + \frac{kx}{t}\) , then
\[(f_{1}\circ f_{2}\circ \cdot \cdot \cdot \circ f_{n})(t) = \frac{A_{n}t + B_{n}}{C_{n}t + D_{n}}.\]
Proof. Straightforward by induction: the \(n = 1\) case is true and for \(n \geq 2\) ,
\[\frac{A_{n - 1}f_{n}(t) + B_{n - 1}}{C_{n - 1}f_{n}(t) + D_{n - 1}} = \frac{A_{n - 1}(t + nx) + B_{n - 1}t}{C_{n - 1}(t + nx) + D_{n - 1}t} = \frac{(A_{n - 1} + B_{n - 1})t + nxA_{n - 1}}{(C_{n - 1} + D_{n - 1})t + nxD_{n - 1}}.\]
It is possible to solve these recurrences algebraically, but there is in fact a nice combinatorial interpretation of these polynomials:
## Lemma
Let \(\mathcal{T}_{n}\) be the set of involutions on \(\{1,2,\ldots ,n\}\) and for \(\pi \in \mathcal{T}_{n}\) , let \(a(\pi)\) denote the number of transpositions in \(\pi\) . Let \(\mathcal{J}_{n} \subseteq \mathcal{T}_{n}\) be the set of involutions \(\pi\) where the minimal fixed point is less than the minimal \(x\) with \(\pi (x) < x\) . Then, for all \(k \geq 1\) , we have
\[A_{n} = \sum_{\pi \in \mathcal{T}_{n}}x^{a(\pi)} B_{n} = \sum_{\pi \in \mathcal{T}_{n + 1}\atop \pi (n + 1)\neq n + 1}x^{a(\pi)}\] \[C_{n} = \sum_{\pi \in \mathcal{J}_{n}}x^{a(\pi)} D_{n} = \sum_{\pi \in \mathcal{J}_{n + 1}\atop \pi (n + 1)\neq n + 1}x^{a(\pi)}.\]
Proof. We use induction on \(n\) , with the case \(n = 1\) being easily verified. For \(n \geq 2\) , note that
\[A_{n} - B_{n - 1} = \sum_{\substack{\pi \in \mathcal{I}_{k + 1} \\ \pi (k + 1) = k + 1}}x^{a(\pi)} = A_{n - 1}.\]
Moreover, every \(\pi \in \mathcal{I}_{n + 1}\) swapping \(n + 1\) with something else can be characterized by one of \(n\) choices for \(\pi (n + 1)\) and an involution on the remaining \(n - 1\) elements. Therefore \(B_{n} = n x A_{n - 1}\) . A similar proof holds for the \(C_{n}\) and \(D_{n}\) . \(\square\)
We now note that
\[\frac{P(x)}{Q(x)} = (f_{1}\circ f_{2}\circ \cdot \cdot \cdot \circ f_{p - 1})(1) = \frac{A_{p - 1} + B_{p - 1}}{C_{p - 1} + D_{p - 1}} = \frac{A_{p}}{C_{p}}.\]
It suffices to show that all nonconstant coefficients of \(A_{p}\) are divisible by \(p\) and that all coefficients of \(C_{p}\) are not divisible by \(p\) . If we show this, then any nonconstant factor dividing \(A_{p}\) must have a leading coefficient divisible by \(p\) (proof: reduce the factorization mod \(p\) ), then any nonconstant factor dividing \(C_{p}\) cannot have a leading coefficient divisible by \(p\) . Moreover, since \(A_{p}\) and \(C_{p}\) have constant terms of 1, they are relatively prime and thus \(P = A_{p}\) and \(Q = C_{p}\) (up to sign).
We now evaluate the coefficients of \(A_{p}\) and \(C_{p}\) . We observe that
\[A_{p} = \sum_{k = 0}^{\frac{p - 1}{2}}\binom{p}{2k}(2k - 1)!!x^{k},\]
and it is easy to see that \(A_{p} \equiv 1\) (mod \(p\) ). Computing the coefficients of \(C_{n}\) is a bit harder. Consider elements of \(\mathcal{J}_{p}\) with \(0 \leq k \leq \frac{p - 1}{2}\) swaps and a minimal fixed point of \(a + 1\) (for \(0 \leq a \leq k\) ). Everything in \(\{1, \ldots , a\}\) must be paired with something greater than \(a + 1\) , and there are \(k - a\) swaps among the remaining elements. It follows that
\[C_{p} = \sum_{k = 0}^{\frac{p - 1}{2}}\sum_{a = 0}^{k}\frac{(p - a - 1)!}{(p - 2a - 1)!}\binom{p - 2a - 1}{2k - 2a}(2k - 2a - 1)!!\cdot x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\sum_{a = 0}^{k}\frac{(p - a - 1)!}{(p - 2k - 1)!2^{k - a}(k - a)!}x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!}\left(\sum_{a = 0}^{k}\frac{1}{2^{k - a}(k - a)!}\prod_{j = 1}^{a}(p - j)\right)x^{k}\] \[\quad \equiv \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!}\left(\sum_{a = 0}^{k}\frac{(-1)^{a}}{2^{k - a}(k - a)!a!}\right)x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!k!}\left(\sum_{a = 0}^{k}\binom{k}{a}\frac{(-1)^{a}}{2^{k - a}}\right)x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!k!}\left(-1 + \frac{1}{2}\right)^{k}x^{k}.\]
The result follows.
Remark. It is not hard to see that \(C_{p}\) simplifies further mod \(p\) to
\[\sum_{k = 0}^{\frac{p - 1}{2}}(-1)^{k}(2k - 1)!!x^{k}.\]
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Let \(p\) be an odd prime number. Suppose \(P\) and \(Q\) are polynomials with integer coefficients such that \(P(0) = Q(0) = 1\) , there is no nonconstant polynomial dividing both \(P\) and \(Q\) , and
\[1 + \frac{x}{1 + \frac{2x}{1 + \frac{\cdots}{1 + (p - 1)x}}} = \frac{P(x)}{Q(x)}.\]
Show that all coefficients of \(P\) except for the constant coefficient are divisible by \(p\) , and all coefficients of \(Q\) are not divisible by \(p\) .
|
\(\P\) Solution 1. We first make some general observations about rational functions represented through continued fractions.
Claim — Let \(a_{1}, a_{2}, \ldots\) , be a sequence of nonzero integers. Define the sequence of polynomials \(P_{1}(x) = 1\) , \(P_{2}(x) = 1 + a_{1}x\) , and
\[P_{k + 1}(x) = P_{k}(x) + a_{k}x P_{k - 1}(x)\]
for \(k \geq 1\) . Then the following properties hold for all \(k \geq 0\) :
- \(P_{k}(0) = 1\) ,
- \(\gcd (P_{k + 1}, P_{k}) = 1\) , and
- \(\deg P_{k} = \lfloor k / 2 \rfloor\) .
\[1 + \frac{a_{k}x}{1 + \frac{a_{k - 1}x}{\ddots}} = \frac{P_{k + 1}(x)}{P_{k}(x)}.\] \[1 + \frac{\ddots}{1 + a_{1}x}\]
Proof. These all follow by induction.
With the setup of the claim, the polynomials \(P\) and \(Q\) in the problem are exactly \(P_{p}\) and \(P_{p}\) for the sequence \(a_{1} = p - 1\) , \(a_{2} = p - 2\) , ..., \(a_{p - 1} = 1\) . From here, we will define \(P\) and \(Q\) in terms of this recurrence and make two transformations on the \(a_{i}\) .
First, subtract \(p\) from each \(a_{i}\) so we now have \(a_{1} = - 1\) , \(a_{2} = - 2\) , ..., \(a_{p - 1} = -(p - 1)\) . The coefficients of \(P\) and \(Q\) only have changed by a multiple of \(p\) . The claim also shows that \(P(0) = Q(0) = 1\) , \(\gcd (P, Q) = 1\) , and the degrees of \(P\) and \(Q\) have not changed, i.e. no leading terms have been added or removed. Therefore it is equivalent to work with this sequence instead.
Similarly, we can multiply \(a_{i}\) by \(- 1\) to get \(a_{1} = 1\) , \(a_{2} = 2\) , ..., \(a_{p - 1} = p - 1\) . This is equivalent to replacing \(x\) with \(- x\) , so some coefficients of \(P\) and \(Q\) are negated by this. The key conditions still remain unchanged.
Remark. For rigor, it's important to prove the facts about continued fractions first rather than going straight to the coefficient replacement as the requirements imposed by the problem statement on \(P\) and \(Q\) are not always preserved modulo \(p\) .
At this point, we are ready to directly calculate the polynomials \(P_{n}\) .
Claim — For all \(n\) , we have
\[P_{n}(x) = \sum_{k\geq 0}\frac{n!}{2^{k}k!(n - 2k)!} x^{k}.\]
Here, we define \(\frac{n!}{(n - 2k)!} = n(n - 1)\ldots (n - 2k + 1)\) so the sum actually stops at \(k = \lfloor n / 2\rfloor\) .
Proof. We use induction. The base cases are clear, and
\[P_{n} + n x P_{n - 1} = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + n x\sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{(n - 1)!}{(n - 2k - 1)!} x^{k}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k - 1)!} x^{k + 1}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} x^{k} + \sum_{k\geq 1}\frac{1}{2^{k - 1}(k - 1)!}\frac{n!}{(n - 2k + 1)!} x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\left[\frac{1}{2^{k}k!}\frac{n!}{(n - 2k)!} +\frac{1}{2^{k - 1}(k - 1)!}\frac{n!}{(n - 2k + 1)!}\right]x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\frac{1}{2^{k}k!}\frac{n!}{(n - 2k + 1)!}\left[(n - 2k + 1) + 2k\right]x^{k}\] \[\qquad = 1 + \sum_{k\geq 1}\frac{1}{2^{k}k!}\frac{(n + 1)!}{(n - 2k + 1)!} x^{k}\] \[\qquad = \sum_{k\geq 0}\frac{1}{2^{k}k!}\frac{(n + 1)!}{(n - 2k + 1)!} x^{k}\] \[\qquad = P_{n + 1}.\]
At this point we can directly check the coefficients of \(P\) and \(Q\) . We have
\[P(x) = P_{p}(x) = \sum_{k\geq 0}\frac{p!}{2^{k}k!(p - 2k)!} x^{k}.\]
For \(k = 0\) , we get a coefficient of 1. For \(k \geq 1\) , the denominator is not a multiple of \(p\) , so the remaining coefficients are multiples of \(p\) . Meanwhile, the coefficients for \(Q\) are \(\frac{(p - 1)!}{2^{k}k!(p - 1 - 2k)!}\) . None of these are divisible by \(p\) because \((p - 1)!\) is not divisible by \(p\) .
Remark. This problem was created from the identity
\[\frac{1}{1 - \frac{x}{1 - \frac{2x}{1 - \frac{3x}{1 - \cdots}}}}\]
You can use this to solve the problem. However, the proof of the identity as well as the details to convert this into the given problem are very lengthy so this is only left as a remark.
## Solution 2.
## Lemma
Define a series of polynomials \(A_{n}\) , \(B_{n}\) , \(C_{n}\) , \(D_{n}\) by letting \(A_{1} = 1\) , \(B_{1} = x\) , \(C_{1} = 1\) , and \(D_{1} = 0\) , and for \(n \geq 2\) ,
\[A_{n} = A_{n - 1} + B_{n - 1} B_{n} = nxA_{n - 1\] \[C_{n} = C_{n - 1} + D_{n - 1} D_{n} = nxC_{n - 1}.\]
Then, if we define \(f_{k}(t) = 1 + \frac{kx}{t}\) , then
\[(f_{1}\circ f_{2}\circ \cdot \cdot \cdot \circ f_{n})(t) = \frac{A_{n}t + B_{n}}{C_{n}t + D_{n}}.\]
Proof. Straightforward by induction: the \(n = 1\) case is true and for \(n \geq 2\) ,
\[\frac{A_{n - 1}f_{n}(t) + B_{n - 1}}{C_{n - 1}f_{n}(t) + D_{n - 1}} = \frac{A_{n - 1}(t + nx) + B_{n - 1}t}{C_{n - 1}(t + nx) + D_{n - 1}t} = \frac{(A_{n - 1} + B_{n - 1})t + nxA_{n - 1}}{(C_{n - 1} + D_{n - 1})t + nxD_{n - 1}}.\]
It is possible to solve these recurrences algebraically, but there is in fact a nice combinatorial interpretation of these polynomials:
## Lemma
Let \(\mathcal{T}_{n}\) be the set of involutions on \(\{1,2,\ldots ,n\}\) and for \(\pi \in \mathcal{T}_{n}\) , let \(a(\pi)\) denote the number of transpositions in \(\pi\) . Let \(\mathcal{J}_{n} \subseteq \mathcal{T}_{n}\) be the set of involutions \(\pi\) where the minimal fixed point is less than the minimal \(x\) with \(\pi (x) < x\) . Then, for all \(k \geq 1\) , we have
\[A_{n} = \sum_{\pi \in \mathcal{T}_{n}}x^{a(\pi)} B_{n} = \sum_{\pi \in \mathcal{T}_{n + 1}\atop \pi (n + 1)\neq n + 1}x^{a(\pi)}\] \[C_{n} = \sum_{\pi \in \mathcal{J}_{n}}x^{a(\pi)} D_{n} = \sum_{\pi \in \mathcal{J}_{n + 1}\atop \pi (n + 1)\neq n + 1}x^{a(\pi)}.\]
Proof. We use induction on \(n\) , with the case \(n = 1\) being easily verified. For \(n \geq 2\) , note that
\[A_{n} - B_{n - 1} = \sum_{\substack{\pi \in \mathcal{I}_{k + 1} \\ \pi (k + 1) = k + 1}}x^{a(\pi)} = A_{n - 1}.\]
Moreover, every \(\pi \in \mathcal{I}_{n + 1}\) swapping \(n + 1\) with something else can be characterized by one of \(n\) choices for \(\pi (n + 1)\) and an involution on the remaining \(n - 1\) elements. Therefore \(B_{n} = n x A_{n - 1}\) . A similar proof holds for the \(C_{n}\) and \(D_{n}\) . \(\square\)
We now note that
\[\frac{P(x)}{Q(x)} = (f_{1}\circ f_{2}\circ \cdot \cdot \cdot \circ f_{p - 1})(1) = \frac{A_{p - 1} + B_{p - 1}}{C_{p - 1} + D_{p - 1}} = \frac{A_{p}}{C_{p}}.\]
It suffices to show that all nonconstant coefficients of \(A_{p}\) are divisible by \(p\) and that all coefficients of \(C_{p}\) are not divisible by \(p\) . If we show this, then any nonconstant factor dividing \(A_{p}\) must have a leading coefficient divisible by \(p\) (proof: reduce the factorization mod \(p\) ), then any nonconstant factor dividing \(C_{p}\) cannot have a leading coefficient divisible by \(p\) . Moreover, since \(A_{p}\) and \(C_{p}\) have constant terms of 1, they are relatively prime and thus \(P = A_{p}\) and \(Q = C_{p}\) (up to sign).
We now evaluate the coefficients of \(A_{p}\) and \(C_{p}\) . We observe that
\[A_{p} = \sum_{k = 0}^{\frac{p - 1}{2}}\binom{p}{2k}(2k - 1)!!x^{k},\]
and it is easy to see that \(A_{p} \equiv 1\) (mod \(p\) ). Computing the coefficients of \(C_{n}\) is a bit harder. Consider elements of \(\mathcal{J}_{p}\) with \(0 \leq k \leq \frac{p - 1}{2}\) swaps and a minimal fixed point of \(a + 1\) (for \(0 \leq a \leq k\) ). Everything in \(\{1, \ldots , a\}\) must be paired with something greater than \(a + 1\) , and there are \(k - a\) swaps among the remaining elements. It follows that
\[C_{p} = \sum_{k = 0}^{\frac{p - 1}{2}}\sum_{a = 0}^{k}\frac{(p - a - 1)!}{(p - 2a - 1)!}\binom{p - 2a - 1}{2k - 2a}(2k - 2a - 1)!!\cdot x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\sum_{a = 0}^{k}\frac{(p - a - 1)!}{(p - 2k - 1)!2^{k - a}(k - a)!}x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!}\left(\sum_{a = 0}^{k}\frac{1}{2^{k - a}(k - a)!}\prod_{j = 1}^{a}(p - j)\right)x^{k}\] \[\quad \equiv \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!}\left(\sum_{a = 0}^{k}\frac{(-1)^{a}}{2^{k - a}(k - a)!a!}\right)x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!k!}\left(\sum_{a = 0}^{k}\binom{k}{a}\frac{(-1)^{a}}{2^{k - a}}\right)x^{k}\] \[\quad = \sum_{k = 0}^{\frac{p - 1}{2}}\frac{(p - 1)!}{(p - 2k - 1)!k!}\left(-1 + \frac{1}{2}\right)^{k}x^{k}.\]
The result follows.
Remark. It is not hard to see that \(C_{p}\) simplifies further mod \(p\) to
\[\sum_{k = 0}^{\frac{p - 1}{2}}(-1)^{k}(2k - 1)!!x^{k}.\]
|
{
"exam": "USA_TSTST",
"problem_label": "2",
"problem_match": "2. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 1.2\\) TSTST 2024/2, proposed by Andrew Gu \n",
"tier": "T0",
"year": "2024"
}
|
Let \(A = \{a_{1},\ldots ,a_{2024}\}\) be a set of 2024 pairwise distinct real numbers. Assume that there exist positive integers \(b_{1},b_{2},\ldots ,b_{2024}\) such that
\[a_{1}b_{1} + a_{2}b_{2} + \cdot \cdot \cdot +a_{2024}b_{2024} = 0.\]
Prove that one can choose \(a_{2025},a_{2026},a_{2027},\ldots\) such that \(a_{k}\in A\) for all \(k\geq 2025\) and, for every positive integer \(d\) , there exist infinitely many positive integers \(n\) satisfying
\[\sum_{k = 1}^{n}a_{k}k^{d} = 0.\]
|
It will be convenient to use 0- based indexing here, i.e. \(A = \{a_{0},\ldots ,a_{2023}\}\) and so on. Let \(m = \sum_{i = 0}^{2023}b_{i}\) . By appending \(b_{i} - 1\) copies of \(a_{i}\) for each \(i\) , we may extend the sequence to \(a_{0},\ldots ,a_{m - 1}\) such that \(a_{0} + \cdot \cdot \cdot +a_{m - 1} = 0\) .
\(\P\) Solution by direct construction. Let \(s_{m}(n)\) be the sum of the base- \(m\) digits of \(n\) , reduced modulo \(m\) . We now claim that \(a_{k} = a_{s_{m}(k)}\) works. It is clear that this extends the original sequence in a valid way.
Claim — Fix \(d\) . Then the sum
\[\sum_{k = 0}^{n - 1}a_{k}(k + 1)^{d}\]
is zero when \(n = cm^{d + 1}\) for any positive integer \(c\) .
If we prove this, then the problem is solved as there are infinitely many possible \(c\) . We have two proofs of this.
Proof of claim by expansion (Andrew Gu). We only need to show that each block of \(m^{d + 1}\) terms sums to zero. Each block takes the form
\[S = \sum_{k = cm^{d + 1}}^{(c + 1)m^{d + 1} - 1}a_{s_{m}(k)}(k + 1)^{d}.\]
We group terms based on the value of \(s_{m}(k)\) . The values of \(k\) in this sum are given by
\[\left\{cm^{d + 1} + \sum_{i = 0}^{d}e_{i}m^{i}\mid (e_{0},\ldots ,e_{d})\in \{0,\ldots ,m - 1\}^{d + 1}\right\} .\]
In this form, the sum of the base- \(m\) digits is \(s_{m}(c) + e_{0} + \dots +e_{d}\) . Therefore we can write
\[S = \sum_{i = 0}^{m - 1}a_{i}\left(\underbrace{\sum_{(e_{0},\dots,e_{d})\in\{0,\dots,m - 1\}^{d + 1}}}_{e_{0} + \dots +e_{d}\equiv i - s_{m}(c)}\underbrace{\left(cm^{d + 1} + 1 + \sum_{j = 0}^{d}e_{j}m^{j}\right)^{d}}_{(2)}\right).\]
Since \(\sum a_{i} = 0\) , it suffices to show that the value of the coefficient given by (1) is independent of \(i\) .
Expand the term (2) with the multinomial theorem. Each monomial in the expansion is a product of terms \(c\) , \(m\) , \(e_{j}\) . Since the exponent is \(d\) , no monomial is divisible by the whole product \(e_{0}e_{1}\dots e_{d}\) . Since the tuples \((e_{0},\ldots ,e_{d})\) are uniformly distributed over all possible tuples when one or more coordinates are removed, that means that the sum of each monomial term is independent of \(i\) . We conclude that the sum (1) is independent of \(i\) as well. \(\square\)
Proof of claim by Fourier transform. Let \(\omega \neq 1\) be an \(m^{\mathrm{th}}\) root of unity. Then, define the operator
\[\Delta_{a}^{(\omega)}f(x) = \sum_{i = 0}^{m - 1}\omega^{i}f(x + ia).\]
By looking at the leading coefficients, one can see that \(\Delta_{a}^{(\omega)}\) lowers the degree of a polynomial by at least \(1\) . As a consequence, by letting \(f(x) = (x + 1)^{d}\) we conclude that
\[\sum_{k\in [0,m_{e})}\omega^{s_{m}(k)}(k + 1)^{d} = (\Delta_{m^{e - 1}}^{(\omega)}\cdot \cdot \cdot \Delta_{m}^{(\omega)}\Delta_{1}^{(\omega)}f)(0) = 0.\]
Since \(a_{1} + \dots +a_{m} = 0\) , by a discrete Fourier transform we may write \(a_{i} = \sum_{j = 1}^{m - 1}c_{j}e^{2\pi ij / m}\) for some \(c_{1},\ldots ,c_{m - 1}\in \mathbb{C}\) . Therefore
\[\sum_{k = 0}^{m^{e} - 1}a_{k}(k + 1)^{d} = \sum_{j = 1}^{m - 1}c_{j}\sum_{k = 0}^{m^{e} - 1}(e^{2\pi ij / m})^{s_{m}(k)}(k + 1)^{d} = 0.\]
Inductive solution. Define \(m\) and extend the sequence to \(a_{m - 1}\) as before. For \(d\geq 0\) , let \(\Sigma_{d}(S)\) denote \(\textstyle \sum_{k\in S}k^{d}\) . Also, for \(d\geq 0\) call a tuple of sets \((S_{0},\ldots ,S_{m - 1})\) to be \(d\) - uniform if for all \(0\leq d^{\prime}\leq d\) we have \(\Sigma_{d^{\prime}}(S_{0}) = \Sigma_{d^{\prime}}(S_{1}) = \dots = \Sigma_{d^{\prime}}(S_{m - 1})\)
## Lemma 1.1
Suppose \((S_{0},\ldots ,S_{m - 1})\) is \(d\) - uniform. Then for all \(0\leq d^{\prime}\leq d + 1\) , \(x\in \mathbb{R}\) , and \(0\leq i,j< m\) , the quantity \(\Sigma_{d^{\prime}}(S_{i} + x) - \Sigma_{d^{\prime}}(S_{j} + x)\) is independent of \(x\) .
Proof. We may expand
\[\Sigma_{d^{\prime}}(S_{i} + x) = \sum_{k = 0}^{d^{\prime}}\binom{d^{\prime}}{k} x^{d^{\prime} - k}\Sigma_{k}(S_{i}).\]
By \(d\) - uniformity, the terms with \(k\leq d\) are independent of \(i\) and go away in the subtraction. The only term left is when \(k = d^{\prime} = d + 1\) . However, this term is independent of \(x\) , as desired. \(\square\)
## Lemma 1.2
Suppose \((S_{0},\ldots ,S_{m - 1})\) is a \(d\) - uniform partition of \([0,n)\) . Then there exists a \((d + 1)\) uniform partition \((S_{0}^{\prime},\ldots ,S_{m - 1}^{\prime})\) of \([0,mn)\) such that \(S_{i}\subseteq S_{i}^{\prime}\) for all \(i\)
Proof. We let \(S_{i}^{\prime} = \bigcup_{k = 0}^{m - 1}(S_{(i + k)\bmod m} + kn)\) . Then, for every \(0\leq d^{\prime}\leq d + 1\) and \(0\leq i,j< m\) , we have
\[\Sigma_{d^{\prime}}(S_{i}^{\prime}) - \Sigma_{d^{\prime}}(S_{j}^{\prime}) = \sum_{k = 0}^{m - 1}\Sigma_{d^{\prime}}(S_{(i + k)\bmod m} + kn) - \Sigma_{d^{\prime}}(S_{(j + k)\bmod m} + kn)\] \[\qquad = \sum_{k = 0}^{m - 1}\Sigma_{d^{\prime}}(S_{(i + k)\bmod m}) - \Sigma_{d^{\prime}}(S_{(j + k)\bmod m})\] \[\qquad = 0.\]
Consider the 0- uniform partition of \([0,m)\) given by \((\{0\} ,\{1\} ,\ldots ,\{m - 1\})\) . By repeatedly applying Lemma 1.2, we get \(d\) - uniform partitions \((S_{0}^{(d)},\ldots ,S_{m - 1}^{(d)})\) of \([0,m^{d + 1})\) such that \(S_{i}^{(d)}\subseteq S_{i}^{(d + 1)}\) for all \(d\) and \(i\) . For every \(k\) , let \(i\) be the unique index such that \(k\in S_{i}^{(d)}\) for some \(d\) , and let \(a_{k} = a_{i}\) . (This doesn't redefine \(a_{0}\) , ..., \(a_{m - 1}\) as for \(k< m\) , we have \(k\in S_{k}^{(0)}\) .) Then, for each \(e\geq d\) , we find that
\[\sum_{k = 0}^{m^{e + 1} - 1}a_{k}(k + 1)^{d} = \sum_{i = 0}^{m - 1}a_{i}\sum_{k\in S_{i}^{(e)}}(k + 1)^{d} = \sum_{i = 0}^{m - 1}a_{i}\sum_{j = 1}^{d}\binom{d}{j}\Sigma_{j}(S_{i}^{(e)}) = 0.\]
Remark. The construction here is essentially the same as the sum- of- digits construction (in fact it would be exactly the same if we replace \((i + k)\) mod \(m\) in the proof of Lemma 1.2 with \((i - k)\) mod \(m\) ). However, it hints at some flexibility in the construction which is less apparent with other approaches. For example, if \(G\) is any transitive subgroup of permutations on \([0,m)\) and \(\pi_{0} = \mathrm{id}\) , \(\pi_{1},\ldots ,\pi_{|G| - 1}\) is an enumeration of the elements of \(G\) , one can turn a \(d\) - uniform partition \((S_{0},\ldots ,S_{m - 1})\) of \([0,n)\) into a \((d + 1)\) - uniform partition \((S_{0}^{\prime},\ldots ,S_{m - 1}^{\prime})\) of \([0,|G|n)\) by letting \(S_{i}^{\prime} = \bigcup_{k = 0}^{|G| - 1}(S_{\pi_{k}(i)} + kn)\) . Here we used the special case \(\pi_{k}(i) = (i + k)\) mod \(m\) ; it may also be natural to let \(G\) be the set of all \(m!\) permutations.
Remark. The construction in the solution has appeared a number of times in the literature; see
- D. H. Lehmer, The Tarry-Escott problem, Scripta Math. 13, 37-41, 1947;
- E. Prouhet, Mémoire sur quelques relations entre les puissances des nombres, C. R. Acad. Sci. Paris 33, 225, 1851;
- E. M. Wright, Equal sums of like powers, Proc. Edinburgh Math. Soc. 2nd series 8, 138-142, 1949;
- E. M. Wright, Prouhet's 1851 solution of the Tarry-Escott problem of 1910, Amer. Math. Monthly 66, 199-201, 1959.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Let \(A = \{a_{1},\ldots ,a_{2024}\}\) be a set of 2024 pairwise distinct real numbers. Assume that there exist positive integers \(b_{1},b_{2},\ldots ,b_{2024}\) such that
\[a_{1}b_{1} + a_{2}b_{2} + \cdot \cdot \cdot +a_{2024}b_{2024} = 0.\]
Prove that one can choose \(a_{2025},a_{2026},a_{2027},\ldots\) such that \(a_{k}\in A\) for all \(k\geq 2025\) and, for every positive integer \(d\) , there exist infinitely many positive integers \(n\) satisfying
\[\sum_{k = 1}^{n}a_{k}k^{d} = 0.\]
|
It will be convenient to use 0- based indexing here, i.e. \(A = \{a_{0},\ldots ,a_{2023}\}\) and so on. Let \(m = \sum_{i = 0}^{2023}b_{i}\) . By appending \(b_{i} - 1\) copies of \(a_{i}\) for each \(i\) , we may extend the sequence to \(a_{0},\ldots ,a_{m - 1}\) such that \(a_{0} + \cdot \cdot \cdot +a_{m - 1} = 0\) .
\(\P\) Solution by direct construction. Let \(s_{m}(n)\) be the sum of the base- \(m\) digits of \(n\) , reduced modulo \(m\) . We now claim that \(a_{k} = a_{s_{m}(k)}\) works. It is clear that this extends the original sequence in a valid way.
Claim — Fix \(d\) . Then the sum
\[\sum_{k = 0}^{n - 1}a_{k}(k + 1)^{d}\]
is zero when \(n = cm^{d + 1}\) for any positive integer \(c\) .
If we prove this, then the problem is solved as there are infinitely many possible \(c\) . We have two proofs of this.
Proof of claim by expansion (Andrew Gu). We only need to show that each block of \(m^{d + 1}\) terms sums to zero. Each block takes the form
\[S = \sum_{k = cm^{d + 1}}^{(c + 1)m^{d + 1} - 1}a_{s_{m}(k)}(k + 1)^{d}.\]
We group terms based on the value of \(s_{m}(k)\) . The values of \(k\) in this sum are given by
\[\left\{cm^{d + 1} + \sum_{i = 0}^{d}e_{i}m^{i}\mid (e_{0},\ldots ,e_{d})\in \{0,\ldots ,m - 1\}^{d + 1}\right\} .\]
In this form, the sum of the base- \(m\) digits is \(s_{m}(c) + e_{0} + \dots +e_{d}\) . Therefore we can write
\[S = \sum_{i = 0}^{m - 1}a_{i}\left(\underbrace{\sum_{(e_{0},\dots,e_{d})\in\{0,\dots,m - 1\}^{d + 1}}}_{e_{0} + \dots +e_{d}\equiv i - s_{m}(c)}\underbrace{\left(cm^{d + 1} + 1 + \sum_{j = 0}^{d}e_{j}m^{j}\right)^{d}}_{(2)}\right).\]
Since \(\sum a_{i} = 0\) , it suffices to show that the value of the coefficient given by (1) is independent of \(i\) .
Expand the term (2) with the multinomial theorem. Each monomial in the expansion is a product of terms \(c\) , \(m\) , \(e_{j}\) . Since the exponent is \(d\) , no monomial is divisible by the whole product \(e_{0}e_{1}\dots e_{d}\) . Since the tuples \((e_{0},\ldots ,e_{d})\) are uniformly distributed over all possible tuples when one or more coordinates are removed, that means that the sum of each monomial term is independent of \(i\) . We conclude that the sum (1) is independent of \(i\) as well. \(\square\)
Proof of claim by Fourier transform. Let \(\omega \neq 1\) be an \(m^{\mathrm{th}}\) root of unity. Then, define the operator
\[\Delta_{a}^{(\omega)}f(x) = \sum_{i = 0}^{m - 1}\omega^{i}f(x + ia).\]
By looking at the leading coefficients, one can see that \(\Delta_{a}^{(\omega)}\) lowers the degree of a polynomial by at least \(1\) . As a consequence, by letting \(f(x) = (x + 1)^{d}\) we conclude that
\[\sum_{k\in [0,m_{e})}\omega^{s_{m}(k)}(k + 1)^{d} = (\Delta_{m^{e - 1}}^{(\omega)}\cdot \cdot \cdot \Delta_{m}^{(\omega)}\Delta_{1}^{(\omega)}f)(0) = 0.\]
Since \(a_{1} + \dots +a_{m} = 0\) , by a discrete Fourier transform we may write \(a_{i} = \sum_{j = 1}^{m - 1}c_{j}e^{2\pi ij / m}\) for some \(c_{1},\ldots ,c_{m - 1}\in \mathbb{C}\) . Therefore
\[\sum_{k = 0}^{m^{e} - 1}a_{k}(k + 1)^{d} = \sum_{j = 1}^{m - 1}c_{j}\sum_{k = 0}^{m^{e} - 1}(e^{2\pi ij / m})^{s_{m}(k)}(k + 1)^{d} = 0.\]
Inductive solution. Define \(m\) and extend the sequence to \(a_{m - 1}\) as before. For \(d\geq 0\) , let \(\Sigma_{d}(S)\) denote \(\textstyle \sum_{k\in S}k^{d}\) . Also, for \(d\geq 0\) call a tuple of sets \((S_{0},\ldots ,S_{m - 1})\) to be \(d\) - uniform if for all \(0\leq d^{\prime}\leq d\) we have \(\Sigma_{d^{\prime}}(S_{0}) = \Sigma_{d^{\prime}}(S_{1}) = \dots = \Sigma_{d^{\prime}}(S_{m - 1})\)
## Lemma 1.1
Suppose \((S_{0},\ldots ,S_{m - 1})\) is \(d\) - uniform. Then for all \(0\leq d^{\prime}\leq d + 1\) , \(x\in \mathbb{R}\) , and \(0\leq i,j< m\) , the quantity \(\Sigma_{d^{\prime}}(S_{i} + x) - \Sigma_{d^{\prime}}(S_{j} + x)\) is independent of \(x\) .
Proof. We may expand
\[\Sigma_{d^{\prime}}(S_{i} + x) = \sum_{k = 0}^{d^{\prime}}\binom{d^{\prime}}{k} x^{d^{\prime} - k}\Sigma_{k}(S_{i}).\]
By \(d\) - uniformity, the terms with \(k\leq d\) are independent of \(i\) and go away in the subtraction. The only term left is when \(k = d^{\prime} = d + 1\) . However, this term is independent of \(x\) , as desired. \(\square\)
## Lemma 1.2
Suppose \((S_{0},\ldots ,S_{m - 1})\) is a \(d\) - uniform partition of \([0,n)\) . Then there exists a \((d + 1)\) uniform partition \((S_{0}^{\prime},\ldots ,S_{m - 1}^{\prime})\) of \([0,mn)\) such that \(S_{i}\subseteq S_{i}^{\prime}\) for all \(i\)
Proof. We let \(S_{i}^{\prime} = \bigcup_{k = 0}^{m - 1}(S_{(i + k)\bmod m} + kn)\) . Then, for every \(0\leq d^{\prime}\leq d + 1\) and \(0\leq i,j< m\) , we have
\[\Sigma_{d^{\prime}}(S_{i}^{\prime}) - \Sigma_{d^{\prime}}(S_{j}^{\prime}) = \sum_{k = 0}^{m - 1}\Sigma_{d^{\prime}}(S_{(i + k)\bmod m} + kn) - \Sigma_{d^{\prime}}(S_{(j + k)\bmod m} + kn)\] \[\qquad = \sum_{k = 0}^{m - 1}\Sigma_{d^{\prime}}(S_{(i + k)\bmod m}) - \Sigma_{d^{\prime}}(S_{(j + k)\bmod m})\] \[\qquad = 0.\]
Consider the 0- uniform partition of \([0,m)\) given by \((\{0\} ,\{1\} ,\ldots ,\{m - 1\})\) . By repeatedly applying Lemma 1.2, we get \(d\) - uniform partitions \((S_{0}^{(d)},\ldots ,S_{m - 1}^{(d)})\) of \([0,m^{d + 1})\) such that \(S_{i}^{(d)}\subseteq S_{i}^{(d + 1)}\) for all \(d\) and \(i\) . For every \(k\) , let \(i\) be the unique index such that \(k\in S_{i}^{(d)}\) for some \(d\) , and let \(a_{k} = a_{i}\) . (This doesn't redefine \(a_{0}\) , ..., \(a_{m - 1}\) as for \(k< m\) , we have \(k\in S_{k}^{(0)}\) .) Then, for each \(e\geq d\) , we find that
\[\sum_{k = 0}^{m^{e + 1} - 1}a_{k}(k + 1)^{d} = \sum_{i = 0}^{m - 1}a_{i}\sum_{k\in S_{i}^{(e)}}(k + 1)^{d} = \sum_{i = 0}^{m - 1}a_{i}\sum_{j = 1}^{d}\binom{d}{j}\Sigma_{j}(S_{i}^{(e)}) = 0.\]
Remark. The construction here is essentially the same as the sum- of- digits construction (in fact it would be exactly the same if we replace \((i + k)\) mod \(m\) in the proof of Lemma 1.2 with \((i - k)\) mod \(m\) ). However, it hints at some flexibility in the construction which is less apparent with other approaches. For example, if \(G\) is any transitive subgroup of permutations on \([0,m)\) and \(\pi_{0} = \mathrm{id}\) , \(\pi_{1},\ldots ,\pi_{|G| - 1}\) is an enumeration of the elements of \(G\) , one can turn a \(d\) - uniform partition \((S_{0},\ldots ,S_{m - 1})\) of \([0,n)\) into a \((d + 1)\) - uniform partition \((S_{0}^{\prime},\ldots ,S_{m - 1}^{\prime})\) of \([0,|G|n)\) by letting \(S_{i}^{\prime} = \bigcup_{k = 0}^{|G| - 1}(S_{\pi_{k}(i)} + kn)\) . Here we used the special case \(\pi_{k}(i) = (i + k)\) mod \(m\) ; it may also be natural to let \(G\) be the set of all \(m!\) permutations.
Remark. The construction in the solution has appeared a number of times in the literature; see
- D. H. Lehmer, The Tarry-Escott problem, Scripta Math. 13, 37-41, 1947;
- E. Prouhet, Mémoire sur quelques relations entre les puissances des nombres, C. R. Acad. Sci. Paris 33, 225, 1851;
- E. M. Wright, Equal sums of like powers, Proc. Edinburgh Math. Soc. 2nd series 8, 138-142, 1949;
- E. M. Wright, Prouhet's 1851 solution of the Tarry-Escott problem of 1910, Amer. Math. Monthly 66, 199-201, 1959.
|
{
"exam": "USA_TSTST",
"problem_label": "3",
"problem_match": "3. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 1.3\\) TSTST 2024/3, proposed by Daniel Zhu \n",
"tier": "T0",
"year": "2024"
}
|
Let \(ABCD\) be a quadrilateral inscribed in a circle with center \(O\) and \(E\) be the intersection of segments \(AC\) and \(BD\) . Let \(\omega_{1}\) be the circumcircle of \(ADE\) and \(\omega_{2}\) be the circumcircle of \(BCE\) . The tangent to \(\omega_{1}\) at \(A\) and the tangent to \(\omega_{2}\) at \(C\) meet at \(P\) . The tangent to \(\omega_{1}\) at \(D\) and the tangent to \(\omega_{2}\) at \(B\) meet at \(Q\) . Show that \(OP = OQ\) .
|
\(\P\) Solution 1. Let \(R = \overline{AD} \cap \overline{BC}\) (possibly at infinity, but we'll see it's an Euclidean point later).

Claim — \(ACRP\) is an isosceles trapezoid with \(\overline{AC} \parallel \overline{PR}\) . Consequently, \(R\) is an Euclidean point, and \(OP = OR\) .
Proof. It is equivalent to show that \(\triangle PAC \cong \triangle RCA\) , or without using \(R\) , that
\[\angle PAC = \angle ACR = \angle ACB, \quad \text{and} \quad \angle PCA = \angle CAR = \angle CAD.\]
Indeed, we have
\[\angle PAC = \angle ADE = \angle ADB = \angle ACB\]
and likewise \(\angle PCA = \angle CAD\) , as requested.
Similarly \(OQ = OR\) , so we're done.
Solution 2.

Let \(PA\) intersect (ABCD) again at \(A^{\prime}\) and let \(QB\) intersect (ABCD) again at \(B^{\prime}\) The problem follows from the following claim.
Claim — \(OA^{\prime}PC \cong ODQB^{\prime}\) .
Proof. We use directed angles mod \(\pi\) . Note that
\[\angle ODQ = \angle ODA + \angle ADQ = \angle DAO + \angle PAD = \angle PAO = \angle OA^{\prime}P,\]
and similarly \(\angle OCP = \angle OB^{\prime}Q\) . Furthermore,
\[\angle A^{\prime}AD = \angle AED = \angle CEB = \angle CBB^{\prime},\]
so \(A^{\prime}D = CB^{\prime}\) , i.e. \(A^{\prime}CDB^{\prime}\) is an isosceles trapezoid. This means \(\angle A^{\prime}OC = \angle DOB^{\prime}\) . Combined with \(OA^{\prime} = OB^{\prime} = OD = DC\) , these three angle equalities imply the congruency. \(\square\)
Solution 3 using complex numbers (Noah Walsh). Use complex numbers with (ABCD) as the unit circle. Because \(PA\) is tangent to (ADE), we have \(\angle PAC = \angle ADB = \frac{1}{2}\angle AOB\) , and therefore
\[\frac{\frac{p - a}{c - a}}{\frac{p - a - 1}{c - a - 1}} = \frac{a}{b\] \[\Rightarrow b\frac{p - a}{c - a} = a\frac{ac\overline{p} - c}{a - c\] \[\Rightarrow bp + a^2 c\overline{p} = ab + ac.\]
The condition that \(PC\) is tangent to (BCE) can be expressed by swapping \(a\) with \(c\) and \(b\) with \(d\) , so we get
\[b p + a^{2}c\overline{{p}} = a b + a c\] \[d p + a c^{2}\overline{{p}} = c d + a c\] \[\Rightarrow p(a d - b c) = a c d + a^{2}c - a b c - a c^{2}\] \[\Rightarrow p = \frac{a c(a + d - b - c)}{a d - b c}.\]
Similarly,
\[q = \frac{bd(a + d - b - c)}{ad - bc}.\]
It is now obvious that \(p\) and \(q\) have the same magnitude.
Remark. One possible trick one might use to compute \(p\) is to compute the coordinates of the points \(A^{\prime},C^{\prime}\in (ABCD)\) such that \(A A^{\prime}\) and \(C C^{\prime}\) are tangent to \((A D E)\) and \((B C E)\) respectively, and then use the chords intersection formula.
If one does this, one gets \(a^{\prime} = a c / b\) and \(c^{\prime} = a c / d\) . At this point, one can simply recognize that \(A^{\prime}\) and \(C^{\prime}\) are the reflection of \(B\) and \(D\) over the perpendicular bisector of \(A C\) , reflect everything over said perpendicular bisector, and suddenly realize that one has solved the problem synthetically.
\(\boxed{ \begin{array}{r l} \end{array} }\) Solution 4 by linearity (Noah Walsh). If \(A E = D E\) the problem is true by symmetry, so we assume \(A E\neq D E\)
Fix \(A\) \(D\) , and \(E\) , and move \(B\) linearly along line \(D E\) . By e.g. Reim's theorem, \(C\) moves linearly as well.
How do we compute \(O\) ? It lies on the perpendicular bisector of \(A D\) , which is fixed. It also lies on the perpendicular bisector of \(B C\) , which is parallel to a fixed line, and passes through the midpoint of \(B C\) , which moves linearly. Therefore, \(O\) moves linearly as well.
Point \(P\) is the intersection of the tangent to \((A D E)\) at \(A\) , which is fixed, and the tangent to \((B C E)\) at \(C\) , which moves linearly, and therefore is linear. Similarly, \(Q\) moves linearly. Therefore, to verify that \(\overrightarrow{O P}\times \overrightarrow{O P} = \overrightarrow{O Q}\times \overrightarrow{O Q}\) , it suffices to check three cases.
The two cases where \(E A = E B\) are trivial by symmetry. We can also check that \(\lim_{B\to \infty_{D E}}\frac{\overrightarrow{O P}\times\overrightarrow{O P}}{\overrightarrow{O Q}\times\overrightarrow{O Q}} = 1\)
Indeed, obviously \(\lim_{B\to \infty_{D E}}\frac{|O P|}{|A P|} = \lim_{B\to \infty_{D E}}\frac{|O Q|}{|D Q|} = 1\) . In addition,
\[\frac{d A P}{d D Q} = \frac{d A P}{d A C}\times \frac{d A C}{d B D}\times \frac{d B D}{d B Q}\] \[\qquad = \frac{\sin\angle A C P}{\sin\angle A P C}\times \frac{d E C}{d E B}\times \frac{\sin\angle B Q D}{\sin\angle B D Q}\] \[\qquad = \frac{\sin\angle A C P}{\sin(\angle A C P + \angle C A P)}\times \frac{\sin\angle E B C}{\sin\angle E C B}\times \frac{\sin(\angle B D Q + \angle D B Q)}{\sin\angle B D Q}\] \[\qquad = \frac{\sin\angle B C E}{\sin(\angle B C E + \angle A D E)}\times \frac{\sin\angle D A E}{\sin\angle A D E}\times \frac{\sin(\angle D A E + \angle E C B)}{\sin\angle E A D}\] \[\qquad = \frac{\sin(\angle D A E + \angle E C B)}{\sin(\angle B C E + \angle A D E)}\] \[\qquad = 1.\]
It follows that \(\lim_{B\to \infty_{D E}}\frac{|A P|}{|D Q|} = 1\) . Therefore,
\[\lim_{B\to \infty_{D E}}\frac{|O P|}{|O Q|} = \lim_{B\to \infty_{D E}}\frac{|O P|}{|A P|}\times \lim_{B\to \infty_{D E}}\frac{|A P|}{|D Q|}\times \lim_{B\to \infty_{D E}}\frac{|D Q|}{|O Q|}\] \[\qquad = 1,\]
which completes the \(B\to \infty_{D E}\) case, and we are done.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let \(ABCD\) be a quadrilateral inscribed in a circle with center \(O\) and \(E\) be the intersection of segments \(AC\) and \(BD\) . Let \(\omega_{1}\) be the circumcircle of \(ADE\) and \(\omega_{2}\) be the circumcircle of \(BCE\) . The tangent to \(\omega_{1}\) at \(A\) and the tangent to \(\omega_{2}\) at \(C\) meet at \(P\) . The tangent to \(\omega_{1}\) at \(D\) and the tangent to \(\omega_{2}\) at \(B\) meet at \(Q\) . Show that \(OP = OQ\) .
|
\(\P\) Solution 1. Let \(R = \overline{AD} \cap \overline{BC}\) (possibly at infinity, but we'll see it's an Euclidean point later).

Claim — \(ACRP\) is an isosceles trapezoid with \(\overline{AC} \parallel \overline{PR}\) . Consequently, \(R\) is an Euclidean point, and \(OP = OR\) .
Proof. It is equivalent to show that \(\triangle PAC \cong \triangle RCA\) , or without using \(R\) , that
\[\angle PAC = \angle ACR = \angle ACB, \quad \text{and} \quad \angle PCA = \angle CAR = \angle CAD.\]
Indeed, we have
\[\angle PAC = \angle ADE = \angle ADB = \angle ACB\]
and likewise \(\angle PCA = \angle CAD\) , as requested.
Similarly \(OQ = OR\) , so we're done.
Solution 2.

Let \(PA\) intersect (ABCD) again at \(A^{\prime}\) and let \(QB\) intersect (ABCD) again at \(B^{\prime}\) The problem follows from the following claim.
Claim — \(OA^{\prime}PC \cong ODQB^{\prime}\) .
Proof. We use directed angles mod \(\pi\) . Note that
\[\angle ODQ = \angle ODA + \angle ADQ = \angle DAO + \angle PAD = \angle PAO = \angle OA^{\prime}P,\]
and similarly \(\angle OCP = \angle OB^{\prime}Q\) . Furthermore,
\[\angle A^{\prime}AD = \angle AED = \angle CEB = \angle CBB^{\prime},\]
so \(A^{\prime}D = CB^{\prime}\) , i.e. \(A^{\prime}CDB^{\prime}\) is an isosceles trapezoid. This means \(\angle A^{\prime}OC = \angle DOB^{\prime}\) . Combined with \(OA^{\prime} = OB^{\prime} = OD = DC\) , these three angle equalities imply the congruency. \(\square\)
Solution 3 using complex numbers (Noah Walsh). Use complex numbers with (ABCD) as the unit circle. Because \(PA\) is tangent to (ADE), we have \(\angle PAC = \angle ADB = \frac{1}{2}\angle AOB\) , and therefore
\[\frac{\frac{p - a}{c - a}}{\frac{p - a - 1}{c - a - 1}} = \frac{a}{b\] \[\Rightarrow b\frac{p - a}{c - a} = a\frac{ac\overline{p} - c}{a - c\] \[\Rightarrow bp + a^2 c\overline{p} = ab + ac.\]
The condition that \(PC\) is tangent to (BCE) can be expressed by swapping \(a\) with \(c\) and \(b\) with \(d\) , so we get
\[b p + a^{2}c\overline{{p}} = a b + a c\] \[d p + a c^{2}\overline{{p}} = c d + a c\] \[\Rightarrow p(a d - b c) = a c d + a^{2}c - a b c - a c^{2}\] \[\Rightarrow p = \frac{a c(a + d - b - c)}{a d - b c}.\]
Similarly,
\[q = \frac{bd(a + d - b - c)}{ad - bc}.\]
It is now obvious that \(p\) and \(q\) have the same magnitude.
Remark. One possible trick one might use to compute \(p\) is to compute the coordinates of the points \(A^{\prime},C^{\prime}\in (ABCD)\) such that \(A A^{\prime}\) and \(C C^{\prime}\) are tangent to \((A D E)\) and \((B C E)\) respectively, and then use the chords intersection formula.
If one does this, one gets \(a^{\prime} = a c / b\) and \(c^{\prime} = a c / d\) . At this point, one can simply recognize that \(A^{\prime}\) and \(C^{\prime}\) are the reflection of \(B\) and \(D\) over the perpendicular bisector of \(A C\) , reflect everything over said perpendicular bisector, and suddenly realize that one has solved the problem synthetically.
\(\boxed{ \begin{array}{r l} \end{array} }\) Solution 4 by linearity (Noah Walsh). If \(A E = D E\) the problem is true by symmetry, so we assume \(A E\neq D E\)
Fix \(A\) \(D\) , and \(E\) , and move \(B\) linearly along line \(D E\) . By e.g. Reim's theorem, \(C\) moves linearly as well.
How do we compute \(O\) ? It lies on the perpendicular bisector of \(A D\) , which is fixed. It also lies on the perpendicular bisector of \(B C\) , which is parallel to a fixed line, and passes through the midpoint of \(B C\) , which moves linearly. Therefore, \(O\) moves linearly as well.
Point \(P\) is the intersection of the tangent to \((A D E)\) at \(A\) , which is fixed, and the tangent to \((B C E)\) at \(C\) , which moves linearly, and therefore is linear. Similarly, \(Q\) moves linearly. Therefore, to verify that \(\overrightarrow{O P}\times \overrightarrow{O P} = \overrightarrow{O Q}\times \overrightarrow{O Q}\) , it suffices to check three cases.
The two cases where \(E A = E B\) are trivial by symmetry. We can also check that \(\lim_{B\to \infty_{D E}}\frac{\overrightarrow{O P}\times\overrightarrow{O P}}{\overrightarrow{O Q}\times\overrightarrow{O Q}} = 1\)
Indeed, obviously \(\lim_{B\to \infty_{D E}}\frac{|O P|}{|A P|} = \lim_{B\to \infty_{D E}}\frac{|O Q|}{|D Q|} = 1\) . In addition,
\[\frac{d A P}{d D Q} = \frac{d A P}{d A C}\times \frac{d A C}{d B D}\times \frac{d B D}{d B Q}\] \[\qquad = \frac{\sin\angle A C P}{\sin\angle A P C}\times \frac{d E C}{d E B}\times \frac{\sin\angle B Q D}{\sin\angle B D Q}\] \[\qquad = \frac{\sin\angle A C P}{\sin(\angle A C P + \angle C A P)}\times \frac{\sin\angle E B C}{\sin\angle E C B}\times \frac{\sin(\angle B D Q + \angle D B Q)}{\sin\angle B D Q}\] \[\qquad = \frac{\sin\angle B C E}{\sin(\angle B C E + \angle A D E)}\times \frac{\sin\angle D A E}{\sin\angle A D E}\times \frac{\sin(\angle D A E + \angle E C B)}{\sin\angle E A D}\] \[\qquad = \frac{\sin(\angle D A E + \angle E C B)}{\sin(\angle B C E + \angle A D E)}\] \[\qquad = 1.\]
It follows that \(\lim_{B\to \infty_{D E}}\frac{|A P|}{|D Q|} = 1\) . Therefore,
\[\lim_{B\to \infty_{D E}}\frac{|O P|}{|O Q|} = \lim_{B\to \infty_{D E}}\frac{|O P|}{|A P|}\times \lim_{B\to \infty_{D E}}\frac{|A P|}{|D Q|}\times \lim_{B\to \infty_{D E}}\frac{|D Q|}{|O Q|}\] \[\qquad = 1,\]
which completes the \(B\to \infty_{D E}\) case, and we are done.
|
{
"exam": "USA_TSTST",
"problem_label": "4",
"problem_match": "4. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 2.1\\) TSTST 2024/4, proposed by Merlijn Staps \n",
"tier": "T0",
"year": "2024"
}
|
For a positive integer \(k\) , let \(s(k)\) denote the number of 1s in the binary representation of \(k\) . Prove that for any positive integer \(n\) ,
\[\sum_{i = 1}^{n}(-1)^{s(3i)} > 0.\]
|
\(\P\) Solution 1. Given a set of positive integers \(S\) , define
\[f(S) = \sum_{k\in S}(-1)^{s(k)}.\]
We also define
\[S_{\mathrm{even}} = \{k\in S\mid k\mathrm{~is~even}\}\] \[S_{\mathrm{odd}} = \{k\in S\mid k\mathrm{~is~odd}\}\]
and apply functions on sets pointwise, e.g.
\[\frac{S - 1}{2} = \left\{\frac{k - 1}{2}\mid k\in S\right\} .\]
The problem follows from the first bullet of the following claim.
Claim — For every positive integer \(n\) ,
\[f(\{3,6,\ldots ,3n\}) > 0\] \[f(\{1,4,\ldots ,3n - 2\})< 0\] \[f(\{2,5,\ldots ,3n - 1\})\leq 0\]
Proof. Induct on \(n\) . The base case \(n = 1\) is easy to check.
For \(S = \{3,6,\ldots ,3n\}\)
\[f(S) = f(S_{\mathrm{even}}) + f(S_{\mathrm{odd}})\] \[\qquad = f(S_{\mathrm{even}} / 2) - f((S_{\mathrm{odd}} - 1) / 2) > 0\]
since the elements of \(S_{\mathrm{even}} / 2\) are 0 mod 3 and the elements of \((S_{\mathrm{odd}} - 1) / 2\) are 1 mod 3.
For \(S = \{1,4,\ldots ,3n - 2\}\)
\[f(S) = f(S_{\mathrm{even}}) + f(S_{\mathrm{odd}})\] \[\qquad = f(S_{\mathrm{even}} / 2) - f((S_{\mathrm{odd}} - 1) / 2)< 0\]
since the elements of \(S_{\mathrm{even}} / 2\) are 2 mod 3 and the elements of \((S_{\mathrm{odd}} - 1) / 2\) are 0 mod 3. (Note that \((S_{\mathrm{odd}} - 1) / 2\) has multiples of 3 starting at 0 rather than 3, but this is fine because \(f(\{3,\ldots ,3n\}) > 0\) clearly implies \(f(\{0,\ldots ,3n\}) > 0\) as well.)
- For \(S = \{2, 5, \ldots , 3n - 1\}\) , there are two cases.
- Case 1: \(2^{2k - 1} \leq 3n - 1 < 2^{2k}\) . Define
\[S_{\mathrm{small}} = \{s \in S \mid s < 2^{2k - 1}\}\] \[S_{\mathrm{big}} = \{s \in S \mid s \geq 2^{2k - 1}\} .\]
Then
\[f(S) = f(S_{\mathrm{small}}) + f(S_{\mathrm{big}})\] \[\qquad = f(S_{\mathrm{small}}) - f(S_{\mathrm{big}} - 2^{2k - 1})< 0\]
since \(S_{\mathrm{big}} - 2^{2k - 1} = \{0, \ldots , 3n - 1 - 2^{2k - 1}\}\) consists of a prefix of the 0 (mod 3) positive integers in addition to 0.
- Case 2: \(2^{2k} < 3n - 1 < 2^{2k + 1}\) . Note that if \(a + b = 2^{2k + 1} - 1\) , then \(f(\{a, b\}) = 0\) . If we use this to cancel out all pairs of numbers in \(S\) which add to \(2^{2k + 1} - 1\) , then we find
\[f(S) = f(\{2, 5, \ldots , 2^{2k + 1} - 3n - 2\}) \leq 0.\]
This completes the induction.
\(\P\) Solution 2. Let
\[f(n) = \sum_{i = 0}^{n}(-1)^{s(3i)},\qquad g(n) = \sum_{i = 0}^{n}(-1)^{s(i)}.\]
Note that the problem is equivalent to showing \(f(n) \geq 2\) for all \(n \geq 1\) .
## Lemma
\(|g(n)| \leq 1\) for all \(n\) .
Proof. Note that \(s(2i + 1) = - s(2i)\) , so \(g(2n + 1) = 0\) and \(g(2n) = (- 1)^{s(2n)}\) by pairing terms. \(\square\)
We will now prove that \(f(n) \geq 2\) for all \(n \geq 1\) by strong induction. We can manually verify \(n \leq 5\) as a base case. For the inductive step, let \(m = \left\lfloor \frac{3n - 3}{4} \right\rfloor\) so that \(4m + 3 \leq n\) . Let \(S = \{0, 3, \ldots , 3n\}\) . Given \(0 \leq k \leq m\) , we can append two digits to the binary representation of \(k\) (equivalently, \(4k + r\) for \(0 \leq r < 4\) ) to get a number in \(S\) . If \(k\) is a multiple of 3, we can append 00 or 11. Otherwise, we can append one of 01 or 10 depending on \(k\) (mod 3). Almost all elements of \(S\) can be covered uniquely in this way, except for at most one missing element. Note that appending 00 or 11 will preserve the parity of the number of 1s while appending 01 or 10 will change the parity. Therefore we can write
\[f(n) \geq 2 \sum_{\substack{0 \leq i \leq m \\ i \equiv 0 \pmod{3}}} (-1)^{s(i)} - \sum_{\substack{0 \leq i \leq m \\ i \not\equiv 0 \pmod{3}}} (-1)^{s(i)} - 1\]
(the \(- 1\) is to account for the possible missing element). Let
\[x = \sum_{\substack{0 \leq i \leq m \\ i \equiv 0 \pmod{3}}} (-1)^{s(i)}, \qquad y = \sum_{\substack{0 \leq i \leq m \\ i \not\equiv 0 \pmod{3}}} (-1)^{s(i)}.\]
According to the lemma, \(|x + y| \leq 1\) . By the inductive hypothesis, \(x \geq 2\) . Therefore
\[f(n) \geq 2x - y - 1 = 3x - (x + y) - 1 \geq 6 - 1 - 1 > 2\]
as desired.
\(\P\) Solution 3. For \(r \in \{0,1,2\}\) , define
\[S_{r}(a,b) = \sum_{\substack{i\in [a,b] \\ i\equiv r\bmod 3}}(-1)^{s(i)},\]
where \(s(i)\) denotes the number of 1s in \(i\) 's binary representation. The problem is equivalent to proving \(S_{0}(0,3n + 1) > 1\) for all \(n \geq 1\) .
## Lemma
For any integer \(d\) , \(S_{r}(0,2^{d})\) is given by:
\[d \mid S_{0}(0,2^{d}) S_{1}(0,2^{d}) S_{2}(0,2^{d})\] \[\mathrm{d o d d} 3^{\frac{d - 1}{2}} -3^{\frac{d - 1}{2}} 0\] \[\mathrm{d e v e n} 2\cdot 3^{\frac{d - 2}{2}} -3^{\frac{d - 2}{2}} -3^{\frac{d - 2}{3}}\]
Proof. Induction with \(d \leq 2\) being clear. For the inductive step, observe that
\[S_{0}(0,2^{d}) = S_{0}(0,2^{d - 1}) + S_{0}(2^{d - 1},2^{d}) = S_{0}(0,2^{d - 1}) - S_{2^{d - 1}}(0,2^{d - 1})\] \[S_{1}(0,2^{d}) = S_{1}(0,2^{d - 1}) + S_{1}(2^{d - 1},2^{d}) = S_{1}(0,2^{d - 1}) - S_{1 + 2^{d - 1}}(0,2^{d - 1})\] \[S_{2}(0,2^{d}) = S_{2}(0,2^{d - 1}) + S_{2}(2^{d - 1},2^{d}) = S_{2}(0,2^{d - 1}) - S_{2 + 2^{d - 1}}(0,2^{d - 1}).\]
Using
\[2^{d - 1} \equiv \begin{cases} 1 \bmod 3 & d \text{odd} \\ 2 \bmod 3 & d \text{even} \end{cases}\]
and applying the inductive hypothesis gives the desired result.
This proves the problem for powers of 2. To prove the problem for general \(n\) , split \([0,3n + 1)\) into blocks
\[[0,3n + 1) = [0,2^{d_{1}})\sqcup [2^{d_{1}},2^{d_{1}} + 2^{d_{2}})\sqcup [2^{d_{1}} + 2^{d_{2}},2^{d_{1}} + 2^{d_{2}} + 2^{d_{3}}),\dots\]
whose lengths are decreasing powers of 2. By the lemma,
\[S_{0}(0,2^{d_{1}}) \geq \begin{cases} 3^{\frac{d_{1} - 1}{2}} & d_{1} \text{odd} \\ 2 \cdot 3^{\frac{d_{1} - 2}{2}} & d_{1} \text{even} \end{cases}\]
\[S_{0}(2^{d_{1}},2^{d_{1}} + 2^{d_{2}}) = -S_{2^{d_{1}}}(0,2^{d_{2}}) \geq 0\]
and for all \(i\) ,
\[S_{0}(2^{d_{1}} + \dots +2^{d_{i - 1}},2^{d_{1}} + \dots +2^{d_{i}}) = (-1)^{i - 1}S_{2^{d_{1}} + \dots +2^{d_{i - 1}}}(0,2^{d_{i}})\] \[\qquad \geq \begin{cases} -2 \cdot 3^{\frac{d_{i} - 2}{2}} & d_{i} \text{even} \\ -1 \cdot 3^{\frac{d_{i} - 1}{2}} & d_{i} \text{odd}. \end{cases}\]
Let \(D = d_{1}\) ; assume \(D \geq 4\) since checking \(D \in \{1, 2, 3\}\) is easy. Summing over all intervals gives
\[S_{0}(0,3n + 1) \geq 2 \cdot 3^{\frac{D - 2}{2}} + 0 - \left(2 \cdot 3^{\frac{D - 4}{2}} + 3^{\frac{D - 4}{2}} + 2 \cdot 3^{\frac{D - 6}{2}} + 3^{\frac{D - 6}{2}} + \dots\right) = 3^{\frac{D - 2}{2}} > 1\]
when \(D\) is even, and
\[S_{0}(0,3n + 1) \geq 3^{\frac{D - 1}{2}} + 0 - \left(3^{\frac{D - 3}{2}} + 2 \cdot 3^{\frac{D - 5}{2}} + 3^{\frac{D - 5}{2}} + 2 \cdot 3^{\frac{D - 7}{2}} + \dots\right) = \frac{1}{2} \cdot 3^{\frac{D - 3}{2}} > 1\]
when \(D\) is odd.
Remark. The following Python code calculates \(\sum_{i = 0}^{n}(- 1)^{s(3i)}\) in \(O(\log n)\) time using digit DP (and in \(O(K \log n)\) time if 3 is replaced by \(K\) ):
import functools
K = 3
def sgn(n: int) - > int:
return - 1 if bin(n).count('1') % 2 else 1
@functools.lru_cache(maxsize=None)
def f(n: int) - > list[int]:
# Returns an array of size K where arr[i] = sum of sgn(j) over 0
<= j <= n with j % K = i
ans = [0] * K
if n == 0:
ans[0] += 1
return ans
x = f(n // 2)
for i in range(K):
ans[2 * i % K] += x[i]
ans[(2 * i + 1) % K] -= x[i]
if n % 2 == 0:
ans[(n + 1) % K] -= sgn(n + 1)
return ans
Remark. Define
\[f(n) = \sum_{i = 0}^{\lfloor n / 3\rfloor}(-1)^{s(3i)}.\]
Then there exist constants \(0 < c_{1} < c_{2}\) such that
\[\lim_{n\to \infty}\inf_{n\log_{4}(3)}\frac{f(n)}{n^{\log_{4}(3)}} = c_{1},\qquad \lim_{n\to \infty}\sup_{n^{\log_{4}(3)}}\frac{f(n)}{n^{\log_{4}(3)}} = c_{2}.\]
The upper constant is \(c_{2} = \frac{2}{3}\) , achieved when \(n\) is a power of 4.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer \(k\) , let \(s(k)\) denote the number of 1s in the binary representation of \(k\) . Prove that for any positive integer \(n\) ,
\[\sum_{i = 1}^{n}(-1)^{s(3i)} > 0.\]
|
\(\P\) Solution 1. Given a set of positive integers \(S\) , define
\[f(S) = \sum_{k\in S}(-1)^{s(k)}.\]
We also define
\[S_{\mathrm{even}} = \{k\in S\mid k\mathrm{~is~even}\}\] \[S_{\mathrm{odd}} = \{k\in S\mid k\mathrm{~is~odd}\}\]
and apply functions on sets pointwise, e.g.
\[\frac{S - 1}{2} = \left\{\frac{k - 1}{2}\mid k\in S\right\} .\]
The problem follows from the first bullet of the following claim.
Claim — For every positive integer \(n\) ,
\[f(\{3,6,\ldots ,3n\}) > 0\] \[f(\{1,4,\ldots ,3n - 2\})< 0\] \[f(\{2,5,\ldots ,3n - 1\})\leq 0\]
Proof. Induct on \(n\) . The base case \(n = 1\) is easy to check.
For \(S = \{3,6,\ldots ,3n\}\)
\[f(S) = f(S_{\mathrm{even}}) + f(S_{\mathrm{odd}})\] \[\qquad = f(S_{\mathrm{even}} / 2) - f((S_{\mathrm{odd}} - 1) / 2) > 0\]
since the elements of \(S_{\mathrm{even}} / 2\) are 0 mod 3 and the elements of \((S_{\mathrm{odd}} - 1) / 2\) are 1 mod 3.
For \(S = \{1,4,\ldots ,3n - 2\}\)
\[f(S) = f(S_{\mathrm{even}}) + f(S_{\mathrm{odd}})\] \[\qquad = f(S_{\mathrm{even}} / 2) - f((S_{\mathrm{odd}} - 1) / 2)< 0\]
since the elements of \(S_{\mathrm{even}} / 2\) are 2 mod 3 and the elements of \((S_{\mathrm{odd}} - 1) / 2\) are 0 mod 3. (Note that \((S_{\mathrm{odd}} - 1) / 2\) has multiples of 3 starting at 0 rather than 3, but this is fine because \(f(\{3,\ldots ,3n\}) > 0\) clearly implies \(f(\{0,\ldots ,3n\}) > 0\) as well.)
- For \(S = \{2, 5, \ldots , 3n - 1\}\) , there are two cases.
- Case 1: \(2^{2k - 1} \leq 3n - 1 < 2^{2k}\) . Define
\[S_{\mathrm{small}} = \{s \in S \mid s < 2^{2k - 1}\}\] \[S_{\mathrm{big}} = \{s \in S \mid s \geq 2^{2k - 1}\} .\]
Then
\[f(S) = f(S_{\mathrm{small}}) + f(S_{\mathrm{big}})\] \[\qquad = f(S_{\mathrm{small}}) - f(S_{\mathrm{big}} - 2^{2k - 1})< 0\]
since \(S_{\mathrm{big}} - 2^{2k - 1} = \{0, \ldots , 3n - 1 - 2^{2k - 1}\}\) consists of a prefix of the 0 (mod 3) positive integers in addition to 0.
- Case 2: \(2^{2k} < 3n - 1 < 2^{2k + 1}\) . Note that if \(a + b = 2^{2k + 1} - 1\) , then \(f(\{a, b\}) = 0\) . If we use this to cancel out all pairs of numbers in \(S\) which add to \(2^{2k + 1} - 1\) , then we find
\[f(S) = f(\{2, 5, \ldots , 2^{2k + 1} - 3n - 2\}) \leq 0.\]
This completes the induction.
\(\P\) Solution 2. Let
\[f(n) = \sum_{i = 0}^{n}(-1)^{s(3i)},\qquad g(n) = \sum_{i = 0}^{n}(-1)^{s(i)}.\]
Note that the problem is equivalent to showing \(f(n) \geq 2\) for all \(n \geq 1\) .
## Lemma
\(|g(n)| \leq 1\) for all \(n\) .
Proof. Note that \(s(2i + 1) = - s(2i)\) , so \(g(2n + 1) = 0\) and \(g(2n) = (- 1)^{s(2n)}\) by pairing terms. \(\square\)
We will now prove that \(f(n) \geq 2\) for all \(n \geq 1\) by strong induction. We can manually verify \(n \leq 5\) as a base case. For the inductive step, let \(m = \left\lfloor \frac{3n - 3}{4} \right\rfloor\) so that \(4m + 3 \leq n\) . Let \(S = \{0, 3, \ldots , 3n\}\) . Given \(0 \leq k \leq m\) , we can append two digits to the binary representation of \(k\) (equivalently, \(4k + r\) for \(0 \leq r < 4\) ) to get a number in \(S\) . If \(k\) is a multiple of 3, we can append 00 or 11. Otherwise, we can append one of 01 or 10 depending on \(k\) (mod 3). Almost all elements of \(S\) can be covered uniquely in this way, except for at most one missing element. Note that appending 00 or 11 will preserve the parity of the number of 1s while appending 01 or 10 will change the parity. Therefore we can write
\[f(n) \geq 2 \sum_{\substack{0 \leq i \leq m \\ i \equiv 0 \pmod{3}}} (-1)^{s(i)} - \sum_{\substack{0 \leq i \leq m \\ i \not\equiv 0 \pmod{3}}} (-1)^{s(i)} - 1\]
(the \(- 1\) is to account for the possible missing element). Let
\[x = \sum_{\substack{0 \leq i \leq m \\ i \equiv 0 \pmod{3}}} (-1)^{s(i)}, \qquad y = \sum_{\substack{0 \leq i \leq m \\ i \not\equiv 0 \pmod{3}}} (-1)^{s(i)}.\]
According to the lemma, \(|x + y| \leq 1\) . By the inductive hypothesis, \(x \geq 2\) . Therefore
\[f(n) \geq 2x - y - 1 = 3x - (x + y) - 1 \geq 6 - 1 - 1 > 2\]
as desired.
\(\P\) Solution 3. For \(r \in \{0,1,2\}\) , define
\[S_{r}(a,b) = \sum_{\substack{i\in [a,b] \\ i\equiv r\bmod 3}}(-1)^{s(i)},\]
where \(s(i)\) denotes the number of 1s in \(i\) 's binary representation. The problem is equivalent to proving \(S_{0}(0,3n + 1) > 1\) for all \(n \geq 1\) .
## Lemma
For any integer \(d\) , \(S_{r}(0,2^{d})\) is given by:
\[d \mid S_{0}(0,2^{d}) S_{1}(0,2^{d}) S_{2}(0,2^{d})\] \[\mathrm{d o d d} 3^{\frac{d - 1}{2}} -3^{\frac{d - 1}{2}} 0\] \[\mathrm{d e v e n} 2\cdot 3^{\frac{d - 2}{2}} -3^{\frac{d - 2}{2}} -3^{\frac{d - 2}{3}}\]
Proof. Induction with \(d \leq 2\) being clear. For the inductive step, observe that
\[S_{0}(0,2^{d}) = S_{0}(0,2^{d - 1}) + S_{0}(2^{d - 1},2^{d}) = S_{0}(0,2^{d - 1}) - S_{2^{d - 1}}(0,2^{d - 1})\] \[S_{1}(0,2^{d}) = S_{1}(0,2^{d - 1}) + S_{1}(2^{d - 1},2^{d}) = S_{1}(0,2^{d - 1}) - S_{1 + 2^{d - 1}}(0,2^{d - 1})\] \[S_{2}(0,2^{d}) = S_{2}(0,2^{d - 1}) + S_{2}(2^{d - 1},2^{d}) = S_{2}(0,2^{d - 1}) - S_{2 + 2^{d - 1}}(0,2^{d - 1}).\]
Using
\[2^{d - 1} \equiv \begin{cases} 1 \bmod 3 & d \text{odd} \\ 2 \bmod 3 & d \text{even} \end{cases}\]
and applying the inductive hypothesis gives the desired result.
This proves the problem for powers of 2. To prove the problem for general \(n\) , split \([0,3n + 1)\) into blocks
\[[0,3n + 1) = [0,2^{d_{1}})\sqcup [2^{d_{1}},2^{d_{1}} + 2^{d_{2}})\sqcup [2^{d_{1}} + 2^{d_{2}},2^{d_{1}} + 2^{d_{2}} + 2^{d_{3}}),\dots\]
whose lengths are decreasing powers of 2. By the lemma,
\[S_{0}(0,2^{d_{1}}) \geq \begin{cases} 3^{\frac{d_{1} - 1}{2}} & d_{1} \text{odd} \\ 2 \cdot 3^{\frac{d_{1} - 2}{2}} & d_{1} \text{even} \end{cases}\]
\[S_{0}(2^{d_{1}},2^{d_{1}} + 2^{d_{2}}) = -S_{2^{d_{1}}}(0,2^{d_{2}}) \geq 0\]
and for all \(i\) ,
\[S_{0}(2^{d_{1}} + \dots +2^{d_{i - 1}},2^{d_{1}} + \dots +2^{d_{i}}) = (-1)^{i - 1}S_{2^{d_{1}} + \dots +2^{d_{i - 1}}}(0,2^{d_{i}})\] \[\qquad \geq \begin{cases} -2 \cdot 3^{\frac{d_{i} - 2}{2}} & d_{i} \text{even} \\ -1 \cdot 3^{\frac{d_{i} - 1}{2}} & d_{i} \text{odd}. \end{cases}\]
Let \(D = d_{1}\) ; assume \(D \geq 4\) since checking \(D \in \{1, 2, 3\}\) is easy. Summing over all intervals gives
\[S_{0}(0,3n + 1) \geq 2 \cdot 3^{\frac{D - 2}{2}} + 0 - \left(2 \cdot 3^{\frac{D - 4}{2}} + 3^{\frac{D - 4}{2}} + 2 \cdot 3^{\frac{D - 6}{2}} + 3^{\frac{D - 6}{2}} + \dots\right) = 3^{\frac{D - 2}{2}} > 1\]
when \(D\) is even, and
\[S_{0}(0,3n + 1) \geq 3^{\frac{D - 1}{2}} + 0 - \left(3^{\frac{D - 3}{2}} + 2 \cdot 3^{\frac{D - 5}{2}} + 3^{\frac{D - 5}{2}} + 2 \cdot 3^{\frac{D - 7}{2}} + \dots\right) = \frac{1}{2} \cdot 3^{\frac{D - 3}{2}} > 1\]
when \(D\) is odd.
Remark. The following Python code calculates \(\sum_{i = 0}^{n}(- 1)^{s(3i)}\) in \(O(\log n)\) time using digit DP (and in \(O(K \log n)\) time if 3 is replaced by \(K\) ):
import functools
K = 3
def sgn(n: int) - > int:
return - 1 if bin(n).count('1') % 2 else 1
@functools.lru_cache(maxsize=None)
def f(n: int) - > list[int]:
# Returns an array of size K where arr[i] = sum of sgn(j) over 0
<= j <= n with j % K = i
ans = [0] * K
if n == 0:
ans[0] += 1
return ans
x = f(n // 2)
for i in range(K):
ans[2 * i % K] += x[i]
ans[(2 * i + 1) % K] -= x[i]
if n % 2 == 0:
ans[(n + 1) % K] -= sgn(n + 1)
return ans
Remark. Define
\[f(n) = \sum_{i = 0}^{\lfloor n / 3\rfloor}(-1)^{s(3i)}.\]
Then there exist constants \(0 < c_{1} < c_{2}\) such that
\[\lim_{n\to \infty}\inf_{n\log_{4}(3)}\frac{f(n)}{n^{\log_{4}(3)}} = c_{1},\qquad \lim_{n\to \infty}\sup_{n^{\log_{4}(3)}}\frac{f(n)}{n^{\log_{4}(3)}} = c_{2}.\]
The upper constant is \(c_{2} = \frac{2}{3}\) , achieved when \(n\) is a power of 4.
|
{
"exam": "USA_TSTST",
"problem_label": "5",
"problem_match": "5. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 2.2\\) TSTST 2024/5, proposed by Holden Mui \n",
"tier": "T0",
"year": "2024"
}
|
Determine whether there exists a function \(f\colon \mathbb{Z}_{>0}\to \mathbb{Z}_{>0}\) such that for all positive integers \(m\) and \(n\) ,
\[f(m + n f(m)) = f(n)^{m} + 2024!\cdot m.\]
|
The answer is no. Let \(P(m,n)\) denote the given FE.
\(\P\) Solution 1 (Gopal Goel). Suppose there was a function \(f\) , and let \(r = f(1)\) . Note that \(P(1,n)\) gives
\[f(1 + r n) = f(n) + 2024!.\]
Iterating this result gives
\[f(1 + r + \dots +r^{k}) = r + k\cdot 2024!\]
for all \(k\in \mathbb{Z}_{\geq 0}\) . If \(r = 1\) , this implies \(f(k + 1) = 1 + k\cdot 2024!\) , which isn't a valid solution, so \(r\geq 2\)
Let \(m = 1 + r + \dots +r^{r^{2}(r - 1)}\) . Note that
\[1 + r + \dots +r^{k} = m + n f(m)\iff \frac{r^{k + 1} - r^{r^{2}(r - 1) + 1}}{r - 1} = n[r + r^{2}(r - 1)2024!].\]
This has a positive integer solution for \(n\) as long as \(k\) is sufficiently large in terms of \(r\) and
\[k\equiv r^{2}(r - 1)\pmod {\phi (1 + r(r - 1)\cdot 2024!)}\]
For such \(k\) , \(P(m,n)\) implies
\[r + k\cdot 2024! = f(n)^{m} + 2024!\cdot m.\]
In particular, \(r + (k - m)\cdot 2024!\) is a perfect \(m\) th power. This has to be true for all \(k\) sufficiently large in an arithmetic progression, which is clearly impossible, as desired.
\(\P\) Solution 2 (Carl Schildkraut). As in the previous solution, we have
\[f(1 + r + \dots +r^{k}) = r + k\cdot 2024!\]
for all \(k\in \mathbb{Z}_{\geq 0}\) , where \(r = f(1)\geq 2\)
Claim — We have \(f(a)\geq \frac{2^{a} - 1}{2024! \cdot a}\) for \(a\in \mathbb{Z}_{>0}\) .
Proof. Let \(c = a + af(a)\) , \(b = f(c) + a\) , and \(d = f(a)\) , so that
\[a + bf(a) = a + af(a) + f(a)f(c) = c + df(c).\]
Comparing \(P(a,b)\) and \(P(c,d)\) tells us
\[f(b)^{a} + 2024!\cdot a = f(d)^{c} + 2024!\cdot c,\]
so
\[f(b)^{a} - \left(f(d)^{1 + f(a)}\right)^{a} = 2024! \cdot af(a).\]
Since the left side of the above equation is positive, it must be at least \(2^{a} - 1\) , which implies the claim. \(\square\)
Plugging in \(a = 1 + r + \dots +r^{k}\) into the above claim immediately gives the desired contradiction, for sufficiently large \(k\) .
\(\P\) Solution 3 (students). If \(f\) existed, then for any \(k\in \mathbb{Z}_{>0}\) we would have
\[f(f(3))^{3 + k f(3)} + 2024!(3 + k f(3)) = f(3 + k f(3) + f(3)f(3 + k f(3)))\] \[\qquad = f(3 + (k + f(3 + k f(3))f(3)))\] \[\qquad = f(k + f(3 + f(3)k))^{3} + 2024!\cdot 3.\]
Choosing \(k = 27(2024!)^{2}f(3)^{2}\) gives
\[f(k + f(3 + f(3)k))^{3} = \left(f(f(3))^{1 + 9(2024!)^{2}f(3)^{3}}\right)^{3} + (3\cdot 2024!f(3))^{3}\]
which contradicts Fermat's last theorem (no two perfect cubes may sum to a perfect cube). Hence \(f\) cannot exist.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists a function \(f\colon \mathbb{Z}_{>0}\to \mathbb{Z}_{>0}\) such that for all positive integers \(m\) and \(n\) ,
\[f(m + n f(m)) = f(n)^{m} + 2024!\cdot m.\]
|
The answer is no. Let \(P(m,n)\) denote the given FE.
\(\P\) Solution 1 (Gopal Goel). Suppose there was a function \(f\) , and let \(r = f(1)\) . Note that \(P(1,n)\) gives
\[f(1 + r n) = f(n) + 2024!.\]
Iterating this result gives
\[f(1 + r + \dots +r^{k}) = r + k\cdot 2024!\]
for all \(k\in \mathbb{Z}_{\geq 0}\) . If \(r = 1\) , this implies \(f(k + 1) = 1 + k\cdot 2024!\) , which isn't a valid solution, so \(r\geq 2\)
Let \(m = 1 + r + \dots +r^{r^{2}(r - 1)}\) . Note that
\[1 + r + \dots +r^{k} = m + n f(m)\iff \frac{r^{k + 1} - r^{r^{2}(r - 1) + 1}}{r - 1} = n[r + r^{2}(r - 1)2024!].\]
This has a positive integer solution for \(n\) as long as \(k\) is sufficiently large in terms of \(r\) and
\[k\equiv r^{2}(r - 1)\pmod {\phi (1 + r(r - 1)\cdot 2024!)}\]
For such \(k\) , \(P(m,n)\) implies
\[r + k\cdot 2024! = f(n)^{m} + 2024!\cdot m.\]
In particular, \(r + (k - m)\cdot 2024!\) is a perfect \(m\) th power. This has to be true for all \(k\) sufficiently large in an arithmetic progression, which is clearly impossible, as desired.
\(\P\) Solution 2 (Carl Schildkraut). As in the previous solution, we have
\[f(1 + r + \dots +r^{k}) = r + k\cdot 2024!\]
for all \(k\in \mathbb{Z}_{\geq 0}\) , where \(r = f(1)\geq 2\)
Claim — We have \(f(a)\geq \frac{2^{a} - 1}{2024! \cdot a}\) for \(a\in \mathbb{Z}_{>0}\) .
Proof. Let \(c = a + af(a)\) , \(b = f(c) + a\) , and \(d = f(a)\) , so that
\[a + bf(a) = a + af(a) + f(a)f(c) = c + df(c).\]
Comparing \(P(a,b)\) and \(P(c,d)\) tells us
\[f(b)^{a} + 2024!\cdot a = f(d)^{c} + 2024!\cdot c,\]
so
\[f(b)^{a} - \left(f(d)^{1 + f(a)}\right)^{a} = 2024! \cdot af(a).\]
Since the left side of the above equation is positive, it must be at least \(2^{a} - 1\) , which implies the claim. \(\square\)
Plugging in \(a = 1 + r + \dots +r^{k}\) into the above claim immediately gives the desired contradiction, for sufficiently large \(k\) .
\(\P\) Solution 3 (students). If \(f\) existed, then for any \(k\in \mathbb{Z}_{>0}\) we would have
\[f(f(3))^{3 + k f(3)} + 2024!(3 + k f(3)) = f(3 + k f(3) + f(3)f(3 + k f(3)))\] \[\qquad = f(3 + (k + f(3 + k f(3))f(3)))\] \[\qquad = f(k + f(3 + f(3)k))^{3} + 2024!\cdot 3.\]
Choosing \(k = 27(2024!)^{2}f(3)^{2}\) gives
\[f(k + f(3 + f(3)k))^{3} = \left(f(f(3))^{1 + 9(2024!)^{2}f(3)^{3}}\right)^{3} + (3\cdot 2024!f(3))^{3}\]
which contradicts Fermat's last theorem (no two perfect cubes may sum to a perfect cube). Hence \(f\) cannot exist.
|
{
"exam": "USA_TSTST",
"problem_label": "6",
"problem_match": "6. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 2.3\\) TSTST 2024/6, proposed by Jaedon Whyte \n",
"tier": "T0",
"year": "2024"
}
|
An infinite sequence \(a_{1},a_{2},a_{3},\ldots\) of real numbers satisfies
\[a_{2n - 1} + a_{2n} > a_{2n + 1} + a_{2n + 2}\qquad \mathrm{and}\qquad a_{2n} + a_{2n + 1}< a_{2n + 2} + a_{2n + 3}\]
for every positive integer \(n\) . Prove that there exists a real number \(C\) such that \(a_{n}a_{n + 1}< C\) for every positive integer \(n\) .
|
Aer \(n\) .
It suffices to solve the problem for sufficiently large \(n\) . Let \(d_{n} = (- 1)^{n - 1}(a_{n + 2} - a_{n})\) . The assertion simply says that \(d_{1}, d_{2}, \ldots\) is strictly increasing.
We consider the following cases.
- Suppose that \(d_{k} > 0\) for some \(k\) . Then,
\[a_{2n + 1} = a_{1} + (d_{1} + d_{3} + \dots +d_{2n - 1})\]
clearly diverges to \(+\infty\) , and
\[a_{2n} = a_{2} - (d_{2} + d_{4} + \dots +d_{2n - 2})\]
clearly diverges to \(-\infty\) , so taking \(C = 0\) works.
- Now assume that \(d_{k} \leq 0\) for all \(k\) . This implies that \((a_{2n + 1})_{n \geq 0}\) is weakly decreasing and \((a_{2n})_{n \geq 1}\) is weakly increasing. Adding the two expressions above together, we see that
\[d_{1} + a_{1} + a_{2}< a_{2n} + a_{2n + 1}< a_{1} + a_{2}.\]
Since \((a_{2n + 1})_{n \geq 0}\) is weakly decreasing, it either diverges to \(-\infty\) or has a finite limit. Similarly, \((a_{2n})_{n \geq 1}\) either diverges to \(+\infty\) or has a finite limit.
- If \((a_{2n + 1})_{n \geq 0}\) diverges to \(-\infty\) , then the first inequality above implies that \((a_{2n})_{n \geq 1}\) must diverge to \(+\infty\) , in which case \(C = 0\) works.
- If \((a_{2n})_{n \geq 1}\) diverges to \(+\infty\) , then the second inequality implies that \((a_{2n + 1})_{n \geq 0}\) must diverge to \(-\infty\) , so again \(C = 0\) works.
- Finally assume that both \(\lim_{n \to \infty} a_{2n + 1}\) and \(\lim_{n \to \infty} a_{2n}\) exist, so the limit \(L = \lim_{n \to \infty} a_{2n} a_{2n + 1}\) also exists. The result follows taking \(C > L\) .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
An infinite sequence \(a_{1},a_{2},a_{3},\ldots\) of real numbers satisfies
\[a_{2n - 1} + a_{2n} > a_{2n + 1} + a_{2n + 2}\qquad \mathrm{and}\qquad a_{2n} + a_{2n + 1}< a_{2n + 2} + a_{2n + 3}\]
for every positive integer \(n\) . Prove that there exists a real number \(C\) such that \(a_{n}a_{n + 1}< C\) for every positive integer \(n\) .
|
Aer \(n\) .
It suffices to solve the problem for sufficiently large \(n\) . Let \(d_{n} = (- 1)^{n - 1}(a_{n + 2} - a_{n})\) . The assertion simply says that \(d_{1}, d_{2}, \ldots\) is strictly increasing.
We consider the following cases.
- Suppose that \(d_{k} > 0\) for some \(k\) . Then,
\[a_{2n + 1} = a_{1} + (d_{1} + d_{3} + \dots +d_{2n - 1})\]
clearly diverges to \(+\infty\) , and
\[a_{2n} = a_{2} - (d_{2} + d_{4} + \dots +d_{2n - 2})\]
clearly diverges to \(-\infty\) , so taking \(C = 0\) works.
- Now assume that \(d_{k} \leq 0\) for all \(k\) . This implies that \((a_{2n + 1})_{n \geq 0}\) is weakly decreasing and \((a_{2n})_{n \geq 1}\) is weakly increasing. Adding the two expressions above together, we see that
\[d_{1} + a_{1} + a_{2}< a_{2n} + a_{2n + 1}< a_{1} + a_{2}.\]
Since \((a_{2n + 1})_{n \geq 0}\) is weakly decreasing, it either diverges to \(-\infty\) or has a finite limit. Similarly, \((a_{2n})_{n \geq 1}\) either diverges to \(+\infty\) or has a finite limit.
- If \((a_{2n + 1})_{n \geq 0}\) diverges to \(-\infty\) , then the first inequality above implies that \((a_{2n})_{n \geq 1}\) must diverge to \(+\infty\) , in which case \(C = 0\) works.
- If \((a_{2n})_{n \geq 1}\) diverges to \(+\infty\) , then the second inequality implies that \((a_{2n + 1})_{n \geq 0}\) must diverge to \(-\infty\) , so again \(C = 0\) works.
- Finally assume that both \(\lim_{n \to \infty} a_{2n + 1}\) and \(\lim_{n \to \infty} a_{2n}\) exist, so the limit \(L = \lim_{n \to \infty} a_{2n} a_{2n + 1}\) also exists. The result follows taking \(C > L\) .
|
{
"exam": "USA_TSTST",
"problem_label": "7",
"problem_match": "7. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 3.1\\) TSTST 2024/7, proposed by Merlijn Staps \n",
"tier": "T0",
"year": "2024"
}
|
Let \(ABC\) be a scalene triangle, and let \(D\) be a point on side \(BC\) satisfying \(\angle BAD = \angle DAC\) . Suppose that \(X\) and \(Y\) are points inside \(ABC\) such that triangles \(ABX\) and \(ACY\) are similar and quadrilaterals \(ACDX\) and \(ABDY\) are cyclic. Let lines \(BX\) and \(CY\) meet at \(S\) and lines \(BY\) and \(CX\) meet at \(T\) . Prove that lines \(DS\) and \(AT\) are parallel.
|
\(\P\) Solution by characterizing \(X\) and \(Y\) . We first state an important property of \(X\) and \(Y\) .
Claim — Points \(X\) and \(Y\) are isogonal conjugates with respect to \(\triangle ABC\) .

Here are two proofs of the claim.
First proof of claim by Maxim Li. We prove an equivalent statement that \(S\) and \(T\) are isogonal conjugates with respect to \(\triangle ABC\) .
First, we note that \(\angle YBC = \angle YAD = \angle XAD = \angle XCB\) , so \(BT = TC\) . Now, let \(T'\) be the isogonal conjugate of \(S\) w.r.t. \(\triangle ABC\) . Since \(\angle ABS = \angle ACS\) , it follows that \(T'B = T'C\) . Thus, both \(T\) and \(T'\) lies on perpendicular bisector of \(BC\) .
Moreover, since \(AX\) and \(AY\) are isogonal with respect to \(\angle BAC\) , by DDIT on point \(A\) and \(BXCY\) , we get that \(AS\) and \(AT\) are isogonal with respect to \(\angle BAC\) . Hence, \(A, T, T'\) are collinear. Since \(\triangle ABC\) is scalene, combining this with the previous paragraph gives \(T = T'\) , or \(S\) and \(T\) are isogonal conjugates. \(\square\)
A second different proof of the claim. Let \(\gamma_{B}\) be the circle through \(B\) and \(C\) tangent to \(AB\) , and define \(\gamma_{C}\) similarly. We claim that \(X\in \gamma_{B}\) and \(Y\in \gamma_{C}\) .
Let \(E\) be the second intersection of \(\gamma_{B}\) with \(A C\) , and let \(F\) be the intersection of \(B E\) and \(A D\) . Consider the transformation \(\tau\) that is the composition of a reflection across \(A D\) and a homothety at \(A\) with ratio \(\frac{A B}{A C}\) . Note that \(\tau\) maps \(Y\mapsto X\) , \(B\mapsto E\) , and \(D\mapsto F\) . Thus, \(X\) lies on \(\tau (\odot (A B D)) = \odot (A E F)\) , so \(X\) is the second intersection of \(\odot (A E F)\) and \(\odot (A D C)\) , i.e. it is the Miquel point of quadrilateral \(C D F E\) . Thus, \(X\) lies on \(\odot (B E C) = \gamma_{B}\) , as claimed.
Finally, the main claim follows from \(\angle B C X = \angle A B X = \angle A C Y\) .
Here are two ways to finish after the claim.
Finish with isosceles trapezoid. We compute
\[\angle A X B = 360^{\circ} - \angle B X C - \angle C X A = 360^{\circ} - \angle B E C - \angle C D A = 180^{\circ} - \frac{\angle A}{2}.\]
Thus, if \(B X\) meets \(\odot (A C D)\) again at \(C^{\prime}\) , then
\[\angle A D C^{\prime} = \angle A X C^{\prime} = \frac{\angle A}{2} = \angle C A D,\]
so \(A D C C^{\prime}\) is an isosceles trapezoid. Similarly, if \(C Y\) meets \(\odot (A B D)\) again at \(B^{\prime}\) , then \(A D B B^{\prime}\) is an isosceles trapezoid. Hence, \(B C C^{\prime}B^{\prime}\) is an isosceles trapezoid whose diagonals meet at \(S\) , so we have that \(S A = S D\) .
However, by the claim, \(S\) and \(T\) are isogonal conjugates in \(A B C\) . Thus,
\[\angle A D S = \angle S A D = \angle D A T,\]
which completes the proof.
Finish with angle chasing (Pitchayut Saengrungkongka). By the claim, let \(\angle D A X =\) \(\angle D A Y = \angle A B X = \angle A C Y = \theta\) . Then,
\[\angle X S Y = \angle A + 2\theta\] \[\angle X D Y = \angle B D Y + \angle C D X - 180^{\circ} = 180^{\circ} - (\angle B A Y + \angle C A X)\] \[\qquad = 180^{\circ} - (\angle A + 2\theta),\]
so \(X S Y D\) is cyclic. Moreover,
\[\angle X T Y = 180^{\circ} - \angle Y B C - \angle X C B = 180^{\circ} - 2\theta = 180^{\circ} - \angle X A Y,\]
so \(A X T Y\) is also cyclic. Finally,
\[\angle (A T,A X) = \angle T Y X = \angle B Y D + \angle D Y X\] \[\qquad = \angle B A D + \angle D S X = \angle B X A + \angle D S X\] \[\qquad = \angle (D S,A X).\]
\(\P\) Solution 2 (Ruben Carpenter). Let \(M\) be the midpoint of \(B C\) , and \(S^{\prime}\) , \(T^{\prime}\) the reflections of \(S\) , \(T\) over \(M\) . In what follows, DDIT is short for the dual of Desargues' involution theorem.
Claim — \(S^{\prime}\) lies on \(A T\) .
Proof. From \(\triangle A B X \sim \triangle A Y C\) , reflection along the angle bisector of \(\angle A B C\) is an involution on the pencil of lines through \(A\) with pairs \((A B,A C)\) , \((A X,A Y)\) and \((A\infty_{B S},A\infty_{C S})\) . By DDIT from \(A\) onto complete quadrilateral \(X Y S T B C\) , \(A S\) is sent to \(A T\) . By DDIT from \(A\) onto \(B C \infty_{B X} \infty_{C Y} S S^{\prime}\) , \((A S,A S^{\prime})\) is also an involutive pair, so \(A S^{\prime} \equiv A T\) . \(\square\)
Claim — \(T^{\prime}\) lies on \(D S\) .
Proof. Using the circles \((A C D X)\) , \((A B D Y)\) we obtain
\[\angle B D T = \angle D A Y = \angle D A C - \angle Y A C = \angle B A D - \angle B A X = \angle X A D = \angle T C B,\]
so \(T\) lies on the perpendicular bisector of \(B C\) . Furthermore
\[\angle C D Y = \angle B A Y = \angle X A C = \angle X D B,\]
so by DDIT from \(D\) onto \(X S Y T B C\) shows \(\angle C D T = \angle S D B\) . The conclusion follows. \(\square\)
Finally, since \(S T S^{\prime}T^{\prime}\) is a parallelogram we immediately have \(D S \parallel A T\) .
Remark. This problem was discovered by taking a degenerate case of IMO 2018/6 in which three of the vertices of the quadrilateral are collinear. Nevertheless, this origin is very obscured in the problem statement and does not seem to help with the solution at all. The original statement asked to show that the midpoints of \(A D\) , \(B C\) , and \(X Y\) are collinear. However, it was found that this is a straightforward consequence of a high- powered result about isogonal conjugates, so the statement was changed.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let \(ABC\) be a scalene triangle, and let \(D\) be a point on side \(BC\) satisfying \(\angle BAD = \angle DAC\) . Suppose that \(X\) and \(Y\) are points inside \(ABC\) such that triangles \(ABX\) and \(ACY\) are similar and quadrilaterals \(ACDX\) and \(ABDY\) are cyclic. Let lines \(BX\) and \(CY\) meet at \(S\) and lines \(BY\) and \(CX\) meet at \(T\) . Prove that lines \(DS\) and \(AT\) are parallel.
|
\(\P\) Solution by characterizing \(X\) and \(Y\) . We first state an important property of \(X\) and \(Y\) .
Claim — Points \(X\) and \(Y\) are isogonal conjugates with respect to \(\triangle ABC\) .

Here are two proofs of the claim.
First proof of claim by Maxim Li. We prove an equivalent statement that \(S\) and \(T\) are isogonal conjugates with respect to \(\triangle ABC\) .
First, we note that \(\angle YBC = \angle YAD = \angle XAD = \angle XCB\) , so \(BT = TC\) . Now, let \(T'\) be the isogonal conjugate of \(S\) w.r.t. \(\triangle ABC\) . Since \(\angle ABS = \angle ACS\) , it follows that \(T'B = T'C\) . Thus, both \(T\) and \(T'\) lies on perpendicular bisector of \(BC\) .
Moreover, since \(AX\) and \(AY\) are isogonal with respect to \(\angle BAC\) , by DDIT on point \(A\) and \(BXCY\) , we get that \(AS\) and \(AT\) are isogonal with respect to \(\angle BAC\) . Hence, \(A, T, T'\) are collinear. Since \(\triangle ABC\) is scalene, combining this with the previous paragraph gives \(T = T'\) , or \(S\) and \(T\) are isogonal conjugates. \(\square\)
A second different proof of the claim. Let \(\gamma_{B}\) be the circle through \(B\) and \(C\) tangent to \(AB\) , and define \(\gamma_{C}\) similarly. We claim that \(X\in \gamma_{B}\) and \(Y\in \gamma_{C}\) .
Let \(E\) be the second intersection of \(\gamma_{B}\) with \(A C\) , and let \(F\) be the intersection of \(B E\) and \(A D\) . Consider the transformation \(\tau\) that is the composition of a reflection across \(A D\) and a homothety at \(A\) with ratio \(\frac{A B}{A C}\) . Note that \(\tau\) maps \(Y\mapsto X\) , \(B\mapsto E\) , and \(D\mapsto F\) . Thus, \(X\) lies on \(\tau (\odot (A B D)) = \odot (A E F)\) , so \(X\) is the second intersection of \(\odot (A E F)\) and \(\odot (A D C)\) , i.e. it is the Miquel point of quadrilateral \(C D F E\) . Thus, \(X\) lies on \(\odot (B E C) = \gamma_{B}\) , as claimed.
Finally, the main claim follows from \(\angle B C X = \angle A B X = \angle A C Y\) .
Here are two ways to finish after the claim.
Finish with isosceles trapezoid. We compute
\[\angle A X B = 360^{\circ} - \angle B X C - \angle C X A = 360^{\circ} - \angle B E C - \angle C D A = 180^{\circ} - \frac{\angle A}{2}.\]
Thus, if \(B X\) meets \(\odot (A C D)\) again at \(C^{\prime}\) , then
\[\angle A D C^{\prime} = \angle A X C^{\prime} = \frac{\angle A}{2} = \angle C A D,\]
so \(A D C C^{\prime}\) is an isosceles trapezoid. Similarly, if \(C Y\) meets \(\odot (A B D)\) again at \(B^{\prime}\) , then \(A D B B^{\prime}\) is an isosceles trapezoid. Hence, \(B C C^{\prime}B^{\prime}\) is an isosceles trapezoid whose diagonals meet at \(S\) , so we have that \(S A = S D\) .
However, by the claim, \(S\) and \(T\) are isogonal conjugates in \(A B C\) . Thus,
\[\angle A D S = \angle S A D = \angle D A T,\]
which completes the proof.
Finish with angle chasing (Pitchayut Saengrungkongka). By the claim, let \(\angle D A X =\) \(\angle D A Y = \angle A B X = \angle A C Y = \theta\) . Then,
\[\angle X S Y = \angle A + 2\theta\] \[\angle X D Y = \angle B D Y + \angle C D X - 180^{\circ} = 180^{\circ} - (\angle B A Y + \angle C A X)\] \[\qquad = 180^{\circ} - (\angle A + 2\theta),\]
so \(X S Y D\) is cyclic. Moreover,
\[\angle X T Y = 180^{\circ} - \angle Y B C - \angle X C B = 180^{\circ} - 2\theta = 180^{\circ} - \angle X A Y,\]
so \(A X T Y\) is also cyclic. Finally,
\[\angle (A T,A X) = \angle T Y X = \angle B Y D + \angle D Y X\] \[\qquad = \angle B A D + \angle D S X = \angle B X A + \angle D S X\] \[\qquad = \angle (D S,A X).\]
\(\P\) Solution 2 (Ruben Carpenter). Let \(M\) be the midpoint of \(B C\) , and \(S^{\prime}\) , \(T^{\prime}\) the reflections of \(S\) , \(T\) over \(M\) . In what follows, DDIT is short for the dual of Desargues' involution theorem.
Claim — \(S^{\prime}\) lies on \(A T\) .
Proof. From \(\triangle A B X \sim \triangle A Y C\) , reflection along the angle bisector of \(\angle A B C\) is an involution on the pencil of lines through \(A\) with pairs \((A B,A C)\) , \((A X,A Y)\) and \((A\infty_{B S},A\infty_{C S})\) . By DDIT from \(A\) onto complete quadrilateral \(X Y S T B C\) , \(A S\) is sent to \(A T\) . By DDIT from \(A\) onto \(B C \infty_{B X} \infty_{C Y} S S^{\prime}\) , \((A S,A S^{\prime})\) is also an involutive pair, so \(A S^{\prime} \equiv A T\) . \(\square\)
Claim — \(T^{\prime}\) lies on \(D S\) .
Proof. Using the circles \((A C D X)\) , \((A B D Y)\) we obtain
\[\angle B D T = \angle D A Y = \angle D A C - \angle Y A C = \angle B A D - \angle B A X = \angle X A D = \angle T C B,\]
so \(T\) lies on the perpendicular bisector of \(B C\) . Furthermore
\[\angle C D Y = \angle B A Y = \angle X A C = \angle X D B,\]
so by DDIT from \(D\) onto \(X S Y T B C\) shows \(\angle C D T = \angle S D B\) . The conclusion follows. \(\square\)
Finally, since \(S T S^{\prime}T^{\prime}\) is a parallelogram we immediately have \(D S \parallel A T\) .
Remark. This problem was discovered by taking a degenerate case of IMO 2018/6 in which three of the vertices of the quadrilateral are collinear. Nevertheless, this origin is very obscured in the problem statement and does not seem to help with the solution at all. The original statement asked to show that the midpoints of \(A D\) , \(B C\) , and \(X Y\) are collinear. However, it was found that this is a straightforward consequence of a high- powered result about isogonal conjugates, so the statement was changed.
|
{
"exam": "USA_TSTST",
"problem_label": "8",
"problem_match": "8. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## \\(\\S 3.2\\) TSTST 2024/8, proposed by Michael Ren \n",
"tier": "T0",
"year": "2024"
}
|
Let \(n \geq 2\) be a fixed integer. The cells of an \(n \times n\) table are filled with the integers from 1 to \(n^2\) with each number appearing exactly once. Let \(N\) be the number of unordered quadruples of cells on this board which form an axis-aligned rectangle, with the two smaller integers being on opposite vertices of this rectangle. Find the largest possible value of \(N\) .
|
L
The largest possible value of \(N\) is \(\frac{1}{12} n^2 (n^2 - 1)\) . Call these rectangles wobbly. We defer the construction until the proof is complete, since the proof suggests the construction.
Proof of bound. Call a triple of integers \((a, b, c)\) an elbow if \(a\) and \(b\) are in the same row, \(b\) and \(c\) are in the same column, and \(a < b > c\) . Observe that the wobbly rectangles are exactly the ones with 2 elbows.
Claim — Every axis- aligned rectangle has at least 1 elbow.
Proof. The smallest integer in any rectangle is the center of an elbow.
Remark. In fact, it is true that any rectangle must have exactly 1 or 2 elbows. However, this fact is not needed in the proof.
Let \(E\) be the number of elbows and \(M\) be the number of non- wobbly rectangles. Then, the number of elbows is at least \(M + 2N = \binom{n}{2}^2 + N\) , so
\[E\geq \binom{n}{2}^{2} + N\iff N\leq E - \binom{n}{2}^{2}.\]
To this end, we will provide an upper bound on \(E\) . For each cell \(c\) , define:
- \(f(c)\) to be the number of cells in \(c\) 's row which are smaller than \(c\) , and
- \(g(c)\) to be the number of cells in \(c\) 's column which are smaller than \(c\) .
Then, the number of elbows centered at \(c\) equals \(f(c)g(c)\) . Thus, the number of elbows satisfies
\[E = \sum_{c}f(c)g(c)\] \[\leq \sum_{c}\frac{1}{2}\big[f(c)^{2} + g(c)^{2}\big]\] \[= n\big(0^{2} + \cdot \cdot \cdot +(n - 1)^{2}\big)\] \[= \frac{n^{2}(n - 1)(2n - 1)}{6}.\]
It follows that the number of wobbly rectangles satisfies
\[N\leq E - \binom{n}{2}^{2}\]
\[= \frac{n^{2}(n - 1)(2n - 1)}{6} -\frac{n^{2}(n - 1)^{2}}{4}\] \[= \frac{n^{2}(n^{2} - 1)}{12}\]
as desired.
Construction. From the proof above, equality holds if and only if \(f(c)=g(c)\) everywhere.
Select any \(n\times n\) Latin square on symbols 0,..., \(n-1\) , and replace the \(n\) copies of symbol \(k\) with the integers \(kn+1,\ldots ,kn+n\) in some order. This construction is valid,because for each cell \(c\) , \(f(c)\) and \(g(c)\) both equal the symbol originally placed in \(c\) .
Here is an example for \(n=6\) . The left grid is the Latin square, and the right grid is one possible table that can be derived from it.
<table><tr><td>0</td><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td></tr><tr><td>5</td><td>0</td><td>1</td><td>2</td><td>3</td><td>4</td></tr><tr><td>4</td><td>5</td><td>0</td><td>1</td><td>2</td><td>3</td></tr><tr><td>3</td><td>4</td><td>5</td><td>0</td><td>1</td><td>2</td></tr><tr><td>2</td><td>3</td><td>4</td><td>5</td><td>0</td><td>1</td></tr><tr><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td><td>0</td></tr></table>
<table><tr><td>1</td><td>7</td><td>13</td><td>19</td><td>25</td><td>31</td></tr><tr><td>32</td><td>2</td><td>8</td><td>14</td><td>20</td><td>26</td></tr><tr><td>27</td><td>33</td><td>3</td><td>9</td><td>15</td><td>21</td></tr><tr><td>22</td><td>28</td><td>34</td><td>4</td><td>10</td><td>16</td></tr><tr><td>17</td><td>23</td><td>29</td><td>35</td><td>5</td><td>11</td></tr><tr><td>12</td><td>18</td><td>24</td><td>30</td><td>36</td><td>6</td></tr></table>
**Remark** (Structure of optimal tables). In fact, any optimal table must lead to a Latin square in a similar way, by reversing the above idea: replace each cell \(c\) with \(f(c)=g(c)\) .
This suggests how to construct all optimal tables: choose any Latin square on 0,..., \(n-1\) , and fill in the cells so that the relative order of cells in every row and column is preserved.
**Remark.** If the grid is filled out in a random order, the expected number of wobbly rectangles is \(\frac {1}{12}n^{2}(n-1)^{2}\) . This is asymptotically equal to the maximum value.
|
\frac{1}{12} n^2 (n^2 - 1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let \(n \geq 2\) be a fixed integer. The cells of an \(n \times n\) table are filled with the integers from 1 to \(n^2\) with each number appearing exactly once. Let \(N\) be the number of unordered quadruples of cells on this board which form an axis-aligned rectangle, with the two smaller integers being on opposite vertices of this rectangle. Find the largest possible value of \(N\) .
|
L
The largest possible value of \(N\) is \(\frac{1}{12} n^2 (n^2 - 1)\) . Call these rectangles wobbly. We defer the construction until the proof is complete, since the proof suggests the construction.
Proof of bound. Call a triple of integers \((a, b, c)\) an elbow if \(a\) and \(b\) are in the same row, \(b\) and \(c\) are in the same column, and \(a < b > c\) . Observe that the wobbly rectangles are exactly the ones with 2 elbows.
Claim — Every axis- aligned rectangle has at least 1 elbow.
Proof. The smallest integer in any rectangle is the center of an elbow.
Remark. In fact, it is true that any rectangle must have exactly 1 or 2 elbows. However, this fact is not needed in the proof.
Let \(E\) be the number of elbows and \(M\) be the number of non- wobbly rectangles. Then, the number of elbows is at least \(M + 2N = \binom{n}{2}^2 + N\) , so
\[E\geq \binom{n}{2}^{2} + N\iff N\leq E - \binom{n}{2}^{2}.\]
To this end, we will provide an upper bound on \(E\) . For each cell \(c\) , define:
- \(f(c)\) to be the number of cells in \(c\) 's row which are smaller than \(c\) , and
- \(g(c)\) to be the number of cells in \(c\) 's column which are smaller than \(c\) .
Then, the number of elbows centered at \(c\) equals \(f(c)g(c)\) . Thus, the number of elbows satisfies
\[E = \sum_{c}f(c)g(c)\] \[\leq \sum_{c}\frac{1}{2}\big[f(c)^{2} + g(c)^{2}\big]\] \[= n\big(0^{2} + \cdot \cdot \cdot +(n - 1)^{2}\big)\] \[= \frac{n^{2}(n - 1)(2n - 1)}{6}.\]
It follows that the number of wobbly rectangles satisfies
\[N\leq E - \binom{n}{2}^{2}\]
\[= \frac{n^{2}(n - 1)(2n - 1)}{6} -\frac{n^{2}(n - 1)^{2}}{4}\] \[= \frac{n^{2}(n^{2} - 1)}{12}\]
as desired.
Construction. From the proof above, equality holds if and only if \(f(c)=g(c)\) everywhere.
Select any \(n\times n\) Latin square on symbols 0,..., \(n-1\) , and replace the \(n\) copies of symbol \(k\) with the integers \(kn+1,\ldots ,kn+n\) in some order. This construction is valid,because for each cell \(c\) , \(f(c)\) and \(g(c)\) both equal the symbol originally placed in \(c\) .
Here is an example for \(n=6\) . The left grid is the Latin square, and the right grid is one possible table that can be derived from it.
<table><tr><td>0</td><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td></tr><tr><td>5</td><td>0</td><td>1</td><td>2</td><td>3</td><td>4</td></tr><tr><td>4</td><td>5</td><td>0</td><td>1</td><td>2</td><td>3</td></tr><tr><td>3</td><td>4</td><td>5</td><td>0</td><td>1</td><td>2</td></tr><tr><td>2</td><td>3</td><td>4</td><td>5</td><td>0</td><td>1</td></tr><tr><td>1</td><td>2</td><td>3</td><td>4</td><td>5</td><td>0</td></tr></table>
<table><tr><td>1</td><td>7</td><td>13</td><td>19</td><td>25</td><td>31</td></tr><tr><td>32</td><td>2</td><td>8</td><td>14</td><td>20</td><td>26</td></tr><tr><td>27</td><td>33</td><td>3</td><td>9</td><td>15</td><td>21</td></tr><tr><td>22</td><td>28</td><td>34</td><td>4</td><td>10</td><td>16</td></tr><tr><td>17</td><td>23</td><td>29</td><td>35</td><td>5</td><td>11</td></tr><tr><td>12</td><td>18</td><td>24</td><td>30</td><td>36</td><td>6</td></tr></table>
**Remark** (Structure of optimal tables). In fact, any optimal table must lead to a Latin square in a similar way, by reversing the above idea: replace each cell \(c\) with \(f(c)=g(c)\) .
This suggests how to construct all optimal tables: choose any Latin square on 0,..., \(n-1\) , and fill in the cells so that the relative order of cells in every row and column is preserved.
**Remark.** If the grid is filled out in a random order, the expected number of wobbly rectangles is \(\frac {1}{12}n^{2}(n-1)^{2}\) . This is asymptotically equal to the maximum value.
|
{
"exam": "USA_TSTST",
"problem_label": "9",
"problem_match": "9. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2024.jsonl",
"solution_match": "## §3.3 TSTST 2024/9 \n",
"tier": "T0",
"year": "2024"
}
|
In a finite group of people, some pairs are friends (friendship is mutual). Each person \(p\) has a list \(f_{1}(p), f_{2}(p), \ldots , f_{d(p)}(p)\) of their friends, where \(d(p)\) is the number of distinct friends \(p\) has. Additionally, any two people are connected by a series of friendships. Each person also has a water balloon. The following game is played until someone ends up with more than one water balloon: on round \(r\) , each person \(p\) throws the current water balloon they have to their friend \(f_{s}(p)\) such that \(d(p)\) divides \(r - s\) . Show that if the game never ends, then everyone has the same number of friends.
|
Given a person \(p\) , let \(F(p)\) be the set of friends of \(p\) . Choose a person \(p\) with the most friends. Note that for each friend \(q\) of \(p\) , \(p\) receives a water balloon from \(q\) once out of every \(d(q)\) turns. Since \(p\) always receives 1 water balloon, we must have
\[\sum_{q\in F(p)}\frac{1}{d(q)} = 1.\]
Since this sum has \(d(p)\) terms, and since \(d(q) \leq d(p)\) for all \(q\) , we have
\[1 \geq d(p) \cdot \frac{1}{d(p)} = 1.\]
Thus we must have equality for all friends \(q\) of \(p\) . In particular, \(d(q) = d(p)\) . Thus all friends of any person with the most number of friends also have the most number of friends.
Again, let \(p\) be a person with the most friends. Now for any other person \(q\) , there exists a sequence of people \(p = p_{0}, p_{1}, \ldots , p_{n} = q\) . Repeatedly applying the previous result gives us \(d(p) = d(p_{0}) = d(p_{1}) = \dots = d(p_{n}) = d(q)\) . Thus any person has the maximum number of friends out of the group, which means that each person has the same number of friends.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a finite group of people, some pairs are friends (friendship is mutual). Each person \(p\) has a list \(f_{1}(p), f_{2}(p), \ldots , f_{d(p)}(p)\) of their friends, where \(d(p)\) is the number of distinct friends \(p\) has. Additionally, any two people are connected by a series of friendships. Each person also has a water balloon. The following game is played until someone ends up with more than one water balloon: on round \(r\) , each person \(p\) throws the current water balloon they have to their friend \(f_{s}(p)\) such that \(d(p)\) divides \(r - s\) . Show that if the game never ends, then everyone has the same number of friends.
|
Given a person \(p\) , let \(F(p)\) be the set of friends of \(p\) . Choose a person \(p\) with the most friends. Note that for each friend \(q\) of \(p\) , \(p\) receives a water balloon from \(q\) once out of every \(d(q)\) turns. Since \(p\) always receives 1 water balloon, we must have
\[\sum_{q\in F(p)}\frac{1}{d(q)} = 1.\]
Since this sum has \(d(p)\) terms, and since \(d(q) \leq d(p)\) for all \(q\) , we have
\[1 \geq d(p) \cdot \frac{1}{d(p)} = 1.\]
Thus we must have equality for all friends \(q\) of \(p\) . In particular, \(d(q) = d(p)\) . Thus all friends of any person with the most number of friends also have the most number of friends.
Again, let \(p\) be a person with the most friends. Now for any other person \(q\) , there exists a sequence of people \(p = p_{0}, p_{1}, \ldots , p_{n} = q\) . Repeatedly applying the previous result gives us \(d(p) = d(p_{0}) = d(p_{1}) = \dots = d(p_{n}) = d(q)\) . Thus any person has the maximum number of friends out of the group, which means that each person has the same number of friends.
|
{
"exam": "IMO",
"problem_label": "1",
"problem_match": "Problem 1. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 1.1\\) Solution to TSTST 1, by Milan Haiman \n",
"tier": "T0",
"year": "2025"
}
|
Find all sets \(S \subseteq \mathbb{Z}\) for which there exists a function \(f: \mathbb{R} \to \mathbb{Z}\) such that
- \(f(x - y) - 2f(x) + f(x + y) \geq -1\) for all \(x, y \in \mathbb{R}\) , and
- \(S = \{f(z) \mid z \in \mathbb{R}\}\) .
|
The answer is \(\{a\}\) , \(\{a,a + 1\}\) , \(\{a,a + 1,a + 2,\ldots \}\) , and \(\mathbb{Z}\) , for arbitrary \(a\in \mathbb{Z}\) . For constructions, it is not hard to show that if \(g\colon \mathbb{R}\to \mathbb{R}\) is a convex function, then \(\lfloor g\rfloor\) satisfies the functional equation. Thus \(f(x) = a\) , \(f(x) = \lfloor x\rfloor\) , and \(f(x) = \lfloor x^{2}\rfloor +a\) work, covering the first, fourth, and third class of answers respectively. Furthermore, it is not hard to show that \(f(x) = a + \mathbf{1}_{x > 0}\) also works to cover the second class.
Let \(P(x,y)\) denote the condition. To prove that nothing else works, the key result is to prove an "intermediate value theorem": if \(a\) and \(b\) are in the range of \(f\) , then so is every integer between \(a\) and \(b\) . Let's first see how this finishes. If we assume the intermediate value theorem, then all we need to show is that if the range of the range of \(f\) is at least 2, then the range of \(f\) is unbounded above. Indeed, if \(f(x) - f(y)\geq 2\) , then \(P(x,y - x)\) gives us that \(f(2x - y) > f(x)\) , so iterating this procedure finishes.
We will now prove the intermediate value theorem. We will repeatedly use the fact that if \(f(x)\) is a solution, so is \(f(ax + b) + c\) for \(a,b\in \mathbb{R}\) and \(c\in \mathbb{Z}\) .
## Lemma 1.1
If \(f(0)\leq - 1\) , then \(f(2^{k})\geq 2^{k}f(1)\) for \(k\geq 0\)
Proof. \(P(2^{k},2^{k})\) yields that \(f(2^{k + 1})\geq 2f(2^{k})\)
## Lemma 1.2
If \(f(- 1)\leq - 2\) and \(f(0) = 0\) , then \(f(2^{k})\geq 2^{k} - 1\) for all positive integers \(k\) .
Proof. Applying Lemma 1.1 to \(f(x - 1) + 1\) yields that \(f(2^{k} - 1)\geq 2^{k} - 1\) . Then, applying Lemma 1.1 to \(f(2^{k} - x) - f(2^{k}) - 1\) yields that
\[f(0) - f(2^{k}) - 1\geq 2^{k}(f(2^{k} - 1) - f(2^{k}) - 1)\implies f(2^{k}) + 1\geq \frac{2^{k}f(2^{k} - 1)}{2^{k} - 1}\geq 2^{k}.\]
Now to prove the intermediate value theorem, scale and shift such that \(f(- 1)\leq - 2\) and \(f(0) = 0\) ; it suffices to show that there exists some number strictly between \(f(- 1)\) and \(f(0)\) in the range of \(f\) (since by iteration we can then get all values). Suppose not and let \(a_{k} = f(- 1 / 2^{k})\) . If \(k\) is minimal such that \(a_{k}\geq 0\) , then \(P(- 1 / 2^{k},1 / 2^{k})\) yields a contradiction. Thus \(a_{k}\leq - 2\) for all \(k\) . However, applying Lemma 1.2 to \(f(x / 2^{k})\) yields that \(a_{k}\leq - 2\implies f(1)\geq 2^{k} - 1\) , which cannot hold for all \(k\) since \(f(1)\) is constant.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all sets \(S \subseteq \mathbb{Z}\) for which there exists a function \(f: \mathbb{R} \to \mathbb{Z}\) such that
- \(f(x - y) - 2f(x) + f(x + y) \geq -1\) for all \(x, y \in \mathbb{R}\) , and
- \(S = \{f(z) \mid z \in \mathbb{R}\}\) .
|
The answer is \(\{a\}\) , \(\{a,a + 1\}\) , \(\{a,a + 1,a + 2,\ldots \}\) , and \(\mathbb{Z}\) , for arbitrary \(a\in \mathbb{Z}\) . For constructions, it is not hard to show that if \(g\colon \mathbb{R}\to \mathbb{R}\) is a convex function, then \(\lfloor g\rfloor\) satisfies the functional equation. Thus \(f(x) = a\) , \(f(x) = \lfloor x\rfloor\) , and \(f(x) = \lfloor x^{2}\rfloor +a\) work, covering the first, fourth, and third class of answers respectively. Furthermore, it is not hard to show that \(f(x) = a + \mathbf{1}_{x > 0}\) also works to cover the second class.
Let \(P(x,y)\) denote the condition. To prove that nothing else works, the key result is to prove an "intermediate value theorem": if \(a\) and \(b\) are in the range of \(f\) , then so is every integer between \(a\) and \(b\) . Let's first see how this finishes. If we assume the intermediate value theorem, then all we need to show is that if the range of the range of \(f\) is at least 2, then the range of \(f\) is unbounded above. Indeed, if \(f(x) - f(y)\geq 2\) , then \(P(x,y - x)\) gives us that \(f(2x - y) > f(x)\) , so iterating this procedure finishes.
We will now prove the intermediate value theorem. We will repeatedly use the fact that if \(f(x)\) is a solution, so is \(f(ax + b) + c\) for \(a,b\in \mathbb{R}\) and \(c\in \mathbb{Z}\) .
## Lemma 1.1
If \(f(0)\leq - 1\) , then \(f(2^{k})\geq 2^{k}f(1)\) for \(k\geq 0\)
Proof. \(P(2^{k},2^{k})\) yields that \(f(2^{k + 1})\geq 2f(2^{k})\)
## Lemma 1.2
If \(f(- 1)\leq - 2\) and \(f(0) = 0\) , then \(f(2^{k})\geq 2^{k} - 1\) for all positive integers \(k\) .
Proof. Applying Lemma 1.1 to \(f(x - 1) + 1\) yields that \(f(2^{k} - 1)\geq 2^{k} - 1\) . Then, applying Lemma 1.1 to \(f(2^{k} - x) - f(2^{k}) - 1\) yields that
\[f(0) - f(2^{k}) - 1\geq 2^{k}(f(2^{k} - 1) - f(2^{k}) - 1)\implies f(2^{k}) + 1\geq \frac{2^{k}f(2^{k} - 1)}{2^{k} - 1}\geq 2^{k}.\]
Now to prove the intermediate value theorem, scale and shift such that \(f(- 1)\leq - 2\) and \(f(0) = 0\) ; it suffices to show that there exists some number strictly between \(f(- 1)\) and \(f(0)\) in the range of \(f\) (since by iteration we can then get all values). Suppose not and let \(a_{k} = f(- 1 / 2^{k})\) . If \(k\) is minimal such that \(a_{k}\geq 0\) , then \(P(- 1 / 2^{k},1 / 2^{k})\) yields a contradiction. Thus \(a_{k}\leq - 2\) for all \(k\) . However, applying Lemma 1.2 to \(f(x / 2^{k})\) yields that \(a_{k}\leq - 2\implies f(1)\geq 2^{k} - 1\) , which cannot hold for all \(k\) since \(f(1)\) is constant.
|
{
"exam": "IMO",
"problem_label": "2",
"problem_match": "Problem 2. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 1.2\\) Solution to TSTST 2, by Daniel Zhu \n",
"tier": "T0",
"year": "2025"
}
|
Let \(a_{1}, a_{2}, r\) , and \(s\) be positive integers with \(r\) and \(s\) odd. The sequence \(a_{1}, a_{2}, a_{3}, \ldots\) is defined by
\[a_{n + 2} = r a_{n + 1} + s a_{n}\]
for all \(n \geq 1\) . Determine the maximum possible number of integers \(1 \leq \ell \leq 2025\) such that \(a_{\ell}\) divides \(a_{\ell +1}\) , over all possible choices of \(a_{1}, a_{2}, r\) , and \(s\) .
|
Answer 1350.
\(\P\) Solution We first provide the upper bound. We start by dividing out any common factors of \(a_{1}\) and \(a_{2}\) from the whole sequence. Note that since \(r\) and \(s\) are odd, and \(a_{1}\) and \(a_{2}\) cannot both be divisible by 2, the sequence \(a_{1}, a_{2}, a_{3}, \ldots\) (mod 2) must be some cyclic shift of the sequence \(1, 1, 0, 1, 1, 0, 1, 1, 0, \ldots\) . This means that exactly \(\frac{2025}{3} = 675\) of the values of \(\ell\) satisfy \(a_{\ell} \equiv 0\) (mod 2) and \(a_{\ell +1} \equiv 1\) (mod 2). An even number can never divide an odd number, so we have an upper bound of \(2025 \times \frac{2}{3} = 1350\) .
Now we provide a construction so that \(a_{\ell}\) divides \(a_{\ell +1}\) for 1350 values of \(\ell\) . Let \(F_{1}, F_{2}, F_{3}, \ldots\) denote the Fibonacci sequence with \(F_{1} = F_{2} = 1\) . Let
\[C = \frac{F_{1} \cdot F_{2} \cdot F_{3} \cdot F_{4} \cdots F_{2025}}{F_{3} \cdot F_{6} \cdot F_{9} \cdot F_{12} \cdots F_{2025}} = F_{1} \cdot F_{2} \cdot F_{4} \cdot F_{5} \cdots F_{2024}.\]
Note that \(C\) is odd, since it is the product of all odd Fibonacci numbers up to \(F_{2025}\) . We let \(a_{n} = C^{n - 1} F_{n}\) , which satisfies the recurrence with \(r = C^{2}\) and \(s = C\) . This gives
\[\frac{a_{\ell +1}}{a_{\ell}} = C \cdot \frac{F_{\ell +1}}{F_{\ell}},\]
which is an integer whenever \(3 \nmid \ell\) for \(1 \leq \ell \leq 2025\) .
|
1350
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let \(a_{1}, a_{2}, r\) , and \(s\) be positive integers with \(r\) and \(s\) odd. The sequence \(a_{1}, a_{2}, a_{3}, \ldots\) is defined by
\[a_{n + 2} = r a_{n + 1} + s a_{n}\]
for all \(n \geq 1\) . Determine the maximum possible number of integers \(1 \leq \ell \leq 2025\) such that \(a_{\ell}\) divides \(a_{\ell +1}\) , over all possible choices of \(a_{1}, a_{2}, r\) , and \(s\) .
|
Answer 1350.
\(\P\) Solution We first provide the upper bound. We start by dividing out any common factors of \(a_{1}\) and \(a_{2}\) from the whole sequence. Note that since \(r\) and \(s\) are odd, and \(a_{1}\) and \(a_{2}\) cannot both be divisible by 2, the sequence \(a_{1}, a_{2}, a_{3}, \ldots\) (mod 2) must be some cyclic shift of the sequence \(1, 1, 0, 1, 1, 0, 1, 1, 0, \ldots\) . This means that exactly \(\frac{2025}{3} = 675\) of the values of \(\ell\) satisfy \(a_{\ell} \equiv 0\) (mod 2) and \(a_{\ell +1} \equiv 1\) (mod 2). An even number can never divide an odd number, so we have an upper bound of \(2025 \times \frac{2}{3} = 1350\) .
Now we provide a construction so that \(a_{\ell}\) divides \(a_{\ell +1}\) for 1350 values of \(\ell\) . Let \(F_{1}, F_{2}, F_{3}, \ldots\) denote the Fibonacci sequence with \(F_{1} = F_{2} = 1\) . Let
\[C = \frac{F_{1} \cdot F_{2} \cdot F_{3} \cdot F_{4} \cdots F_{2025}}{F_{3} \cdot F_{6} \cdot F_{9} \cdot F_{12} \cdots F_{2025}} = F_{1} \cdot F_{2} \cdot F_{4} \cdot F_{5} \cdots F_{2024}.\]
Note that \(C\) is odd, since it is the product of all odd Fibonacci numbers up to \(F_{2025}\) . We let \(a_{n} = C^{n - 1} F_{n}\) , which satisfies the recurrence with \(r = C^{2}\) and \(s = C\) . This gives
\[\frac{a_{\ell +1}}{a_{\ell}} = C \cdot \frac{F_{\ell +1}}{F_{\ell}},\]
which is an integer whenever \(3 \nmid \ell\) for \(1 \leq \ell \leq 2025\) .
|
{
"exam": "IMO",
"problem_label": "3",
"problem_match": "Problem 3. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## §1.3 Solution to TSTST 3, by Carlos Rodriguez, Albert Wang, Kevin Wu, Isaac Zhu, Nathan Cho \n",
"tier": "T0",
"year": "2025"
}
|
Let \(n \geq 2\) be a positive integer. Let \(a_{1}, a_{2}, \ldots , a_{n}\) be a sequence of positive integers such that
\[\gcd (a_{1},a_{2}),\gcd (a_{2},a_{3}),\ldots ,\gcd (a_{n - 1},a_{n})\]
is a strictly increasing sequence. Find, in terms of \(n\) , the maximum possible value of
\[\frac{1}{a_{1}} +\frac{1}{a_{2}} +\dots +\frac{1}{a_{n}}\]
over all such sequences.
|
We claim the maximum possible value is 2. To see that this is achievable, let the sequence \((a_{i})_{i = 1}^{n}\) be 1, 2, 4, ..., \(2^{n - 2}\) , \(2^{n - 2}\) . Then \(\gcd (a_{i},a_{i + 1}) = 2^{i - 1}\) , which is an increasing sequence, and it is easy to check that \(\sum \frac{1}{a_{i}} = 2\) . We now show this is the maximum.
Let \(d_{i} = \gcd (a_{i},a_{i + 1})\) . Since \(d_{i - 1}< d_{i}\) , we have that \(\frac{a_{i}}{d_{i - 1}} >\frac{a_{i}}{d_{i}}\) . But these are both integers, so we get that
\[1\leq \frac{a_{i}}{d_{i - 1}} -\frac{a_{i}}{d_{i}}\Longrightarrow \frac{1}{a_{i}}\leq \frac{1}{d_{i - 1}} -\frac{1}{d_{i}}.\]
Adding everything up, we get that
\[\sum_{i = 1}^{n}\frac{1}{a_{i}}\leq \frac{1}{a_{1}} +\frac{1}{d_{1}} -\frac{1}{d_{n - 1}} +\frac{1}{a_{n}}.\]
But \(d_{n - 1}\mid a_{n}\) , so \(d_{n - 1}\leq a_{n}\) , and \(\frac{1}{d_{n - 1}}\geq \frac{1}{a_{n}}\) . Thus, this sum is at most \(\frac{1}{a_{1}} +\frac{1}{d_{1}}\leq 2\) . \(\square\)
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let \(n \geq 2\) be a positive integer. Let \(a_{1}, a_{2}, \ldots , a_{n}\) be a sequence of positive integers such that
\[\gcd (a_{1},a_{2}),\gcd (a_{2},a_{3}),\ldots ,\gcd (a_{n - 1},a_{n})\]
is a strictly increasing sequence. Find, in terms of \(n\) , the maximum possible value of
\[\frac{1}{a_{1}} +\frac{1}{a_{2}} +\dots +\frac{1}{a_{n}}\]
over all such sequences.
|
We claim the maximum possible value is 2. To see that this is achievable, let the sequence \((a_{i})_{i = 1}^{n}\) be 1, 2, 4, ..., \(2^{n - 2}\) , \(2^{n - 2}\) . Then \(\gcd (a_{i},a_{i + 1}) = 2^{i - 1}\) , which is an increasing sequence, and it is easy to check that \(\sum \frac{1}{a_{i}} = 2\) . We now show this is the maximum.
Let \(d_{i} = \gcd (a_{i},a_{i + 1})\) . Since \(d_{i - 1}< d_{i}\) , we have that \(\frac{a_{i}}{d_{i - 1}} >\frac{a_{i}}{d_{i}}\) . But these are both integers, so we get that
\[1\leq \frac{a_{i}}{d_{i - 1}} -\frac{a_{i}}{d_{i}}\Longrightarrow \frac{1}{a_{i}}\leq \frac{1}{d_{i - 1}} -\frac{1}{d_{i}}.\]
Adding everything up, we get that
\[\sum_{i = 1}^{n}\frac{1}{a_{i}}\leq \frac{1}{a_{1}} +\frac{1}{d_{1}} -\frac{1}{d_{n - 1}} +\frac{1}{a_{n}}.\]
But \(d_{n - 1}\mid a_{n}\) , so \(d_{n - 1}\leq a_{n}\) , and \(\frac{1}{d_{n - 1}}\geq \frac{1}{a_{n}}\) . Thus, this sum is at most \(\frac{1}{a_{1}} +\frac{1}{d_{1}}\leq 2\) . \(\square\)
|
{
"exam": "IMO",
"problem_label": "4",
"problem_match": "Problem 4. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 2.1\\) Solution to TSTST 4, by Maxim Li \n",
"tier": "T0",
"year": "2025"
}
|
A tetrahedron \(ABCD\) is said to be angelic if it has nonzero volume and satisfies
\[\angle BAC + \angle CAD + \angle DAB = \angle ABC + \angle CBD + \angle DBA,\] \[\angle ACB + \angle BCD + \angle DCA = \angle ADB + \angle BDC + \angle CDA.\]
Across all angelic tetrahedrons, what is the maximum number of distinct lengths that could appear in the set \(\{AB, AC, AD, BC, BD, CD\}\) ?
|

We claim the maximum cardinality is \(\boxed{4}\) . This is attained by taking a non- square rectangle (or parallelogram) \(A C B D\) and folding it along diagonal \(A B\) , creating edges \(A B\) and \(C D\) in the process. Here, \(A C = B D\) and \(A D = B C\) , while every other length is distinct in the general case. This tetrahedron is congruent to itself under the permutation of vertices \((A,B,C,D)\mapsto (B,A,D,C)\) , and we can verify that the required angle conditions follow from this symmetry.

In the other direction, let \(f(X)\) denote the sum of the angles at \(X\) , so the conditions of the problem statement can be written as \(f(A) = f(B)\) and \(f(C) = f(D)\) . Unfold the three faces that meet at \(D\) to create a net of the tetrahedron. Along with the face \(\triangle A B C\) , we also create the faces \(\triangle A B D_{1}\) , \(\triangle B C D_{2}\) , and \(\triangle A C D_{3}\) . Note that
\(f(A) + f(B) + f(C) + f(D)\) is the sum of all of the angles of all four faces of the tetrahedron, which is \(720^{\circ}\) . Therefore, \(f(A) = f(B) = 360^{\circ} - f(C) = 360^{\circ} - f(D)\) . Furthermore, we have that \(\angle D_{1}AD_{3} = f(A)\) and \(\angle D_{2}CD_{3} = 360^{\circ} - f(C)\) . Since \(AD_{1} = AD_{3}\) and \(CD_{2} = CD_{3}\) by the definition of unfolding, this gives \(\triangle D_{3}AD_{1} \sim \triangle D_{3}CD_{2}\) . Thus, due to spiral similarity, we have \(\triangle D_{3}AC \sim \triangle D_{3}D_{1}D_{2}\) .
Similarly, we also have \(\triangle D_{2}BD_{1} \sim \triangle D_{2}CD_{3} \Rightarrow \triangle CBD_{2} \sim \triangle D_{3}D_{1}D_{2}\) . This means that \(\triangle CBD_{2} \sim \triangle D_{3}AC\) , and since \(CD_{3} = CD_{2}\) , the two triangles are actually congruent. Therefore, \(AC = BD_{2} = BD\) and \(BC = AD_{3} = AD\) . Since we have two pairs of equal edge lengths, the number of distinct edge lengths is at most 4, as desired.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A tetrahedron \(ABCD\) is said to be angelic if it has nonzero volume and satisfies
\[\angle BAC + \angle CAD + \angle DAB = \angle ABC + \angle CBD + \angle DBA,\] \[\angle ACB + \angle BCD + \angle DCA = \angle ADB + \angle BDC + \angle CDA.\]
Across all angelic tetrahedrons, what is the maximum number of distinct lengths that could appear in the set \(\{AB, AC, AD, BC, BD, CD\}\) ?
|

We claim the maximum cardinality is \(\boxed{4}\) . This is attained by taking a non- square rectangle (or parallelogram) \(A C B D\) and folding it along diagonal \(A B\) , creating edges \(A B\) and \(C D\) in the process. Here, \(A C = B D\) and \(A D = B C\) , while every other length is distinct in the general case. This tetrahedron is congruent to itself under the permutation of vertices \((A,B,C,D)\mapsto (B,A,D,C)\) , and we can verify that the required angle conditions follow from this symmetry.

In the other direction, let \(f(X)\) denote the sum of the angles at \(X\) , so the conditions of the problem statement can be written as \(f(A) = f(B)\) and \(f(C) = f(D)\) . Unfold the three faces that meet at \(D\) to create a net of the tetrahedron. Along with the face \(\triangle A B C\) , we also create the faces \(\triangle A B D_{1}\) , \(\triangle B C D_{2}\) , and \(\triangle A C D_{3}\) . Note that
\(f(A) + f(B) + f(C) + f(D)\) is the sum of all of the angles of all four faces of the tetrahedron, which is \(720^{\circ}\) . Therefore, \(f(A) = f(B) = 360^{\circ} - f(C) = 360^{\circ} - f(D)\) . Furthermore, we have that \(\angle D_{1}AD_{3} = f(A)\) and \(\angle D_{2}CD_{3} = 360^{\circ} - f(C)\) . Since \(AD_{1} = AD_{3}\) and \(CD_{2} = CD_{3}\) by the definition of unfolding, this gives \(\triangle D_{3}AD_{1} \sim \triangle D_{3}CD_{2}\) . Thus, due to spiral similarity, we have \(\triangle D_{3}AC \sim \triangle D_{3}D_{1}D_{2}\) .
Similarly, we also have \(\triangle D_{2}BD_{1} \sim \triangle D_{2}CD_{3} \Rightarrow \triangle CBD_{2} \sim \triangle D_{3}D_{1}D_{2}\) . This means that \(\triangle CBD_{2} \sim \triangle D_{3}AC\) , and since \(CD_{3} = CD_{2}\) , the two triangles are actually congruent. Therefore, \(AC = BD_{2} = BD\) and \(BC = AD_{3} = AD\) . Since we have two pairs of equal edge lengths, the number of distinct edge lengths is at most 4, as desired.
|
{
"exam": "IMO",
"problem_label": "5",
"problem_match": "Problem 5. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 2.2\\) Solution to TSTST 5, by Karthik Vedula \n",
"tier": "T0",
"year": "2025"
}
|
Alice and Bob play a game on \(n\) vertices labelled \(1, 2, \ldots , n\) . They take turns adding edges \(\{i, j\}\) , with Alice going first. Neither player is allowed to make a move that creates a cycle, and the game ends after \(n - 1\) total turns.
Let the weight of the edge \(\{i, j\}\) be \(|i - j|\) , and let \(W\) be the total weight of all edges at the end of the game. Alice plays to maximize \(W\) and Bob plays to minimize \(W\) . If both play optimally, what will \(W\) be?
|
\(\P\) Solution Let \(k = \lceil \frac{n - 1}{2}\rceil\) . The answer is
\[\frac{1}{2} (k + 1)(2n - k - 2) = (n - k - 1) + (n - k) + \dots +(n - 1).\]
When \(n = 1\) , this is clear.
Consider now when \(n\geq 2\) . Note that the game consists of \(n - 1\) moves, with Alice making \(k\) moves and Bob making \(n - k - 1\) moves.
We first show Alice can guarantee a total of at least \(\textstyle {\frac{1}{2}}(k + 1)(2n - k - 2)\)
Claim — Alice can ensure her \(i\) th move is an edge of weight at least \(n - i\)
Proof. On her first move, Alice chooses the edge \((1,n)\) , which has weight \(n - 1\) . Now, consider the \(i\) th move, for \(i > 1\) .
Consider the induced subgraph on vertices \(\{1,\ldots ,i\} \sqcup \{n - i + 1,\ldots ,n\}\) . (Note that \(i< n - i + 1\) for all \(1\leq i\leq k\) .) Before Alice's \(i\) th move, exactly \(2i - 2\) moves have been made, so since this subgraph has \(2i\) vertices, it is disconnected.
Take a vertex \(j\) such that \(j\) and 1 are in different connected components. Since Alice's first move is \((1,n)\) , \(j\) is also not connected to \(n\) . Now, if \(j\in \{1,\ldots ,i\}\) , Alice adds \((j,n)\) , otherwise Alice adds \((1,j)\) . \(\square\)
Since each of Bob's edges has weight at least 1, his edges in total have weight at least \(n - k - 1\) . Thus, Alice can ensure a total weight of at least \((n - k - 1) + (n - k) + \dots +(n - 1)\) .
We now give a strategy for Bob.
Claim — Bob can ensure that for each \(1\leq i\leq k\) , there are at most \(i\) edges of weight at least \(n - i\) , while only adding edges of weight 1.
Proof. For \(i = 1\) , this is clear. Consider \(i > 1\) . As above, consider the induced subgraph on vertices \(\{1,\ldots ,i\} \sqcup \{n - i + 1,\ldots ,n\}\) before Bob's \((i - 1)\) st move.
We show that there exists some edge of weight 1 in this subgraph that Bob can choose. Suppose not. Then, since none of \((1,2),\ldots ,(i - 1,i)\) are valid moves, the vertices \(1,\ldots ,i\) are connected. Likewise, the vertices \((n - i + 1,\ldots ,n)\) are connected.
Hence, there are at least \(2(i - 1)\) edges in this subgraph. However, only \(2i - 3\) moves have been played up to this point, contradiction. So, Bob can choose an edge of weight 1 in this subgraph.
When \(n\) is even, Bob makes \(k - 1\) moves, so this accounts for all his moves. When \(n\) is odd, on the final move, since not all the vertices are connected, there exists some edge of weight 1 that Bob can add.
Thus, Bob can select only edges of weight 1. Now, following the above strategy, for any \(1 \leq i \leq k\) , Bob chooses at least \(k - 1\) edges in the induced subgraph on vertices \(\{1, \ldots , i\} \cup \{n - i + 1, \ldots , n\}\) . Since the induced subgraph contains no cycles, Alice plays at most \((2i - 1) - (i - 1) = i\) edges in this subgraph.
Now, note that any edge of weight at least \(n - i\) must have both vertices contained in this subgraph. Thus, there are at most \(i\) edges of weight at least \(n - i\) , as desired. (When \(n > 2\) , \(n - i \geq n - k > 1\) , and when \(n = 2\) , Bob plays no edges, so the bound still holds.) \(\square\)
Using the above strategy, the total weight of Bob's edges is \(n - k - 1\) . Let \(a_{i}\) be the number of edges Alice plays of weight at least \(i\) . Then, the total weight of Alice's edges is
\[\sum_{i = 1}^{n - 1}a_{i}\leq k(n - k - 1) + \sum_{i = n - k}^{n - 1}a_{i}\] \[\qquad \leq k(n - k - 1) + (k + (k - 1) + \cdot \cdot \cdot +1)\] \[\qquad = (n - 1) + (n - 2) + \cdot \cdot \cdot +(n - k).\]
Thus, Bob can ensure a total weight of at most \((n - k - 1) + (n - k) + \dots +(n - 1)\) .
|
\frac{1}{2} (k + 1)(2n - k - 2)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice and Bob play a game on \(n\) vertices labelled \(1, 2, \ldots , n\) . They take turns adding edges \(\{i, j\}\) , with Alice going first. Neither player is allowed to make a move that creates a cycle, and the game ends after \(n - 1\) total turns.
Let the weight of the edge \(\{i, j\}\) be \(|i - j|\) , and let \(W\) be the total weight of all edges at the end of the game. Alice plays to maximize \(W\) and Bob plays to minimize \(W\) . If both play optimally, what will \(W\) be?
|
\(\P\) Solution Let \(k = \lceil \frac{n - 1}{2}\rceil\) . The answer is
\[\frac{1}{2} (k + 1)(2n - k - 2) = (n - k - 1) + (n - k) + \dots +(n - 1).\]
When \(n = 1\) , this is clear.
Consider now when \(n\geq 2\) . Note that the game consists of \(n - 1\) moves, with Alice making \(k\) moves and Bob making \(n - k - 1\) moves.
We first show Alice can guarantee a total of at least \(\textstyle {\frac{1}{2}}(k + 1)(2n - k - 2)\)
Claim — Alice can ensure her \(i\) th move is an edge of weight at least \(n - i\)
Proof. On her first move, Alice chooses the edge \((1,n)\) , which has weight \(n - 1\) . Now, consider the \(i\) th move, for \(i > 1\) .
Consider the induced subgraph on vertices \(\{1,\ldots ,i\} \sqcup \{n - i + 1,\ldots ,n\}\) . (Note that \(i< n - i + 1\) for all \(1\leq i\leq k\) .) Before Alice's \(i\) th move, exactly \(2i - 2\) moves have been made, so since this subgraph has \(2i\) vertices, it is disconnected.
Take a vertex \(j\) such that \(j\) and 1 are in different connected components. Since Alice's first move is \((1,n)\) , \(j\) is also not connected to \(n\) . Now, if \(j\in \{1,\ldots ,i\}\) , Alice adds \((j,n)\) , otherwise Alice adds \((1,j)\) . \(\square\)
Since each of Bob's edges has weight at least 1, his edges in total have weight at least \(n - k - 1\) . Thus, Alice can ensure a total weight of at least \((n - k - 1) + (n - k) + \dots +(n - 1)\) .
We now give a strategy for Bob.
Claim — Bob can ensure that for each \(1\leq i\leq k\) , there are at most \(i\) edges of weight at least \(n - i\) , while only adding edges of weight 1.
Proof. For \(i = 1\) , this is clear. Consider \(i > 1\) . As above, consider the induced subgraph on vertices \(\{1,\ldots ,i\} \sqcup \{n - i + 1,\ldots ,n\}\) before Bob's \((i - 1)\) st move.
We show that there exists some edge of weight 1 in this subgraph that Bob can choose. Suppose not. Then, since none of \((1,2),\ldots ,(i - 1,i)\) are valid moves, the vertices \(1,\ldots ,i\) are connected. Likewise, the vertices \((n - i + 1,\ldots ,n)\) are connected.
Hence, there are at least \(2(i - 1)\) edges in this subgraph. However, only \(2i - 3\) moves have been played up to this point, contradiction. So, Bob can choose an edge of weight 1 in this subgraph.
When \(n\) is even, Bob makes \(k - 1\) moves, so this accounts for all his moves. When \(n\) is odd, on the final move, since not all the vertices are connected, there exists some edge of weight 1 that Bob can add.
Thus, Bob can select only edges of weight 1. Now, following the above strategy, for any \(1 \leq i \leq k\) , Bob chooses at least \(k - 1\) edges in the induced subgraph on vertices \(\{1, \ldots , i\} \cup \{n - i + 1, \ldots , n\}\) . Since the induced subgraph contains no cycles, Alice plays at most \((2i - 1) - (i - 1) = i\) edges in this subgraph.
Now, note that any edge of weight at least \(n - i\) must have both vertices contained in this subgraph. Thus, there are at most \(i\) edges of weight at least \(n - i\) , as desired. (When \(n > 2\) , \(n - i \geq n - k > 1\) , and when \(n = 2\) , Bob plays no edges, so the bound still holds.) \(\square\)
Using the above strategy, the total weight of Bob's edges is \(n - k - 1\) . Let \(a_{i}\) be the number of edges Alice plays of weight at least \(i\) . Then, the total weight of Alice's edges is
\[\sum_{i = 1}^{n - 1}a_{i}\leq k(n - k - 1) + \sum_{i = n - k}^{n - 1}a_{i}\] \[\qquad \leq k(n - k - 1) + (k + (k - 1) + \cdot \cdot \cdot +1)\] \[\qquad = (n - 1) + (n - 2) + \cdot \cdot \cdot +(n - k).\]
Thus, Bob can ensure a total weight of at most \((n - k - 1) + (n - k) + \dots +(n - 1)\) .
|
{
"exam": "IMO",
"problem_label": "6",
"problem_match": "Problem 6. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 2.3\\) Solution to TSTST 6, by Max Lu, Kevin Wu \n",
"tier": "T0",
"year": "2025"
}
|
For a positive real number \(c\) , the sequence \(a_{1}, a_{2}, \ldots\) of real numbers is defined as follows. Let \(a_{1} = c\) , and for \(n \geq 2\) , let
\[a_{n} = \sum_{i = 1}^{n - 1}(a_{i})^{n - i + 1}.\]
Find all positive real numbers \(c\) such that \(a_{i} > a_{i + 1}\) for all positive integers \(i\) .
|
\(\P\) Solution (author) The answer is \(c< \frac{\sqrt{5} - 1}{2}\)
To show this is necessary, note that \(a_{2} = c^{2}\) and \(a_{3} = c^{3} + c^{4}\) , so if the sequence is decreasing, we have \(c^{2} > c^{3} + c^{4}\) , implying \(c< \frac{\sqrt{5} - 1}{2}\)
In the other direction, suppose \(c\) is a positive real number with \(c< \frac{\sqrt{5} - 1}{2}\) . We will apply strong induction. We have
\[a_1 = c\] \[a_2 = c^2\] \[a_3 = c^3 +c^4\]
so \(a_{1} > a_{2}\) (since \(c< 1\) ) and \(a_{2} > a_{3}\) (since \(c< \frac{\sqrt{5} - 1}{2}\) ). For the inductive step, we'll show \(a_{n} > a_{n + 1}\) assuming that \(n\geq 3\) and \(a_{i} > a_{i + 1}\) for all \(i< n\) . We have
\[a_{1}^{n} = c^{n} > c^{n}(c + c^{2}) > c^{n}(c + c^{n}) = a_{1}^{n + 1} + a_{2}^{n}.\]
Also, since \(a_{i} > a_{i + 1}\) for \(i = 2,\ldots ,n - 1\) , we have
\[\sum_{i = 2}^{n - 1}a_{i}^{n - i + 1} > \sum_{i = 2}^{n - 1}a_{i + 1}^{n - i + 1} = \sum_{j = 3}^{n}a_{j}^{n - j + 2},\]
where the equality comes from shifting indices to take \(j = i + 1\) . Thus
\[a_{n} = a_{1}^{n} + \sum_{i = 2}^{n - 1}a_{i}^{n - i + 1} > a_{1}^{n + 1} + a_{2}^{n} + \sum_{j = 3}^{n}a_{j}^{n - j + 2} = a_{n + 1},\]
as desired. This completes the induction step, finishing the solution.
Remark (author). The behavior of the sequence for other values of \(c\) is interesting. In particular, computer experiments seem to indicate that, for \(c = 0.655736876792\) , the sequence starting from \(a_{2}\) increases to a value barely less than \(\frac{1}{2}\) and then decreases, going to 0 as \(n\to \infty\) , while for \(c = 0.655736876793\) , the sequence starting from \(a_{2}\) is increasing and goes to infinity. We conjecture that some form of these patterns hold in general, and that there should exist some value of \(c\) with \(0.655736876792< c< 0.655736876793\) so that the sequence starting from \(a_{2}\) is increasing and \(\lim_{n\to \infty}a_{n} = \frac{1}{2}\) .
\(\parallel\) Solution (Pitchayut) We get \(c< \frac{\sqrt{5} - 1}{2}\) in the same way as the first solution. To show that any such \(c\) gives a strictly decreasing sequence, we use induction on \(n\) . The base cases of \(n = 1,2\) are clear. Let \(t = \frac{\sqrt{5} - 1}{2}\) , then \(t^{2} + t = 1\) . For the inductive step, assume \(n\geq 3\) and \(a_{1} > a_{2} > \dots >a_{n - 1}\) . Since \(t > a_{1}\) , \(t\) is greater than \(a_{1},a_{2},\ldots ,a_{n - 1}\) . Furthermore, \(t^{2} > a_{1}^{2} = a_{2}\geq a_{n - 1}\) . Thus
\[a_{n} = a_{1}^{n} + a_{2}^{n - 1} + \dots +a_{n - 1}^{2}\] \[\qquad < t(a_{1}^{n - 1} + a_{2}^{n - 2} + \dots +a_{n - 2}^{2}) + t^{2}a_{n - 1}\] \[\qquad = t a_{n - 1} + t^{2}a_{n - 1}\] \[\qquad = a_{n - 1},\]
as desired.
|
c< \frac{\sqrt{5} - 1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a positive real number \(c\) , the sequence \(a_{1}, a_{2}, \ldots\) of real numbers is defined as follows. Let \(a_{1} = c\) , and for \(n \geq 2\) , let
\[a_{n} = \sum_{i = 1}^{n - 1}(a_{i})^{n - i + 1}.\]
Find all positive real numbers \(c\) such that \(a_{i} > a_{i + 1}\) for all positive integers \(i\) .
|
\(\P\) Solution (author) The answer is \(c< \frac{\sqrt{5} - 1}{2}\)
To show this is necessary, note that \(a_{2} = c^{2}\) and \(a_{3} = c^{3} + c^{4}\) , so if the sequence is decreasing, we have \(c^{2} > c^{3} + c^{4}\) , implying \(c< \frac{\sqrt{5} - 1}{2}\)
In the other direction, suppose \(c\) is a positive real number with \(c< \frac{\sqrt{5} - 1}{2}\) . We will apply strong induction. We have
\[a_1 = c\] \[a_2 = c^2\] \[a_3 = c^3 +c^4\]
so \(a_{1} > a_{2}\) (since \(c< 1\) ) and \(a_{2} > a_{3}\) (since \(c< \frac{\sqrt{5} - 1}{2}\) ). For the inductive step, we'll show \(a_{n} > a_{n + 1}\) assuming that \(n\geq 3\) and \(a_{i} > a_{i + 1}\) for all \(i< n\) . We have
\[a_{1}^{n} = c^{n} > c^{n}(c + c^{2}) > c^{n}(c + c^{n}) = a_{1}^{n + 1} + a_{2}^{n}.\]
Also, since \(a_{i} > a_{i + 1}\) for \(i = 2,\ldots ,n - 1\) , we have
\[\sum_{i = 2}^{n - 1}a_{i}^{n - i + 1} > \sum_{i = 2}^{n - 1}a_{i + 1}^{n - i + 1} = \sum_{j = 3}^{n}a_{j}^{n - j + 2},\]
where the equality comes from shifting indices to take \(j = i + 1\) . Thus
\[a_{n} = a_{1}^{n} + \sum_{i = 2}^{n - 1}a_{i}^{n - i + 1} > a_{1}^{n + 1} + a_{2}^{n} + \sum_{j = 3}^{n}a_{j}^{n - j + 2} = a_{n + 1},\]
as desired. This completes the induction step, finishing the solution.
Remark (author). The behavior of the sequence for other values of \(c\) is interesting. In particular, computer experiments seem to indicate that, for \(c = 0.655736876792\) , the sequence starting from \(a_{2}\) increases to a value barely less than \(\frac{1}{2}\) and then decreases, going to 0 as \(n\to \infty\) , while for \(c = 0.655736876793\) , the sequence starting from \(a_{2}\) is increasing and goes to infinity. We conjecture that some form of these patterns hold in general, and that there should exist some value of \(c\) with \(0.655736876792< c< 0.655736876793\) so that the sequence starting from \(a_{2}\) is increasing and \(\lim_{n\to \infty}a_{n} = \frac{1}{2}\) .
\(\parallel\) Solution (Pitchayut) We get \(c< \frac{\sqrt{5} - 1}{2}\) in the same way as the first solution. To show that any such \(c\) gives a strictly decreasing sequence, we use induction on \(n\) . The base cases of \(n = 1,2\) are clear. Let \(t = \frac{\sqrt{5} - 1}{2}\) , then \(t^{2} + t = 1\) . For the inductive step, assume \(n\geq 3\) and \(a_{1} > a_{2} > \dots >a_{n - 1}\) . Since \(t > a_{1}\) , \(t\) is greater than \(a_{1},a_{2},\ldots ,a_{n - 1}\) . Furthermore, \(t^{2} > a_{1}^{2} = a_{2}\geq a_{n - 1}\) . Thus
\[a_{n} = a_{1}^{n} + a_{2}^{n - 1} + \dots +a_{n - 1}^{2}\] \[\qquad < t(a_{1}^{n - 1} + a_{2}^{n - 2} + \dots +a_{n - 2}^{2}) + t^{2}a_{n - 1}\] \[\qquad = t a_{n - 1} + t^{2}a_{n - 1}\] \[\qquad = a_{n - 1},\]
as desired.
|
{
"exam": "IMO",
"problem_label": "7",
"problem_match": "Problem 7. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 3.1\\) Solution to TSTST 7, by Luke Robitaille \n",
"tier": "T0",
"year": "2025"
}
|
Find all polynomials \(f\) with integer coefficients such that for all positive integers \(n\) ,
\[n \text{ divides } \frac{f(f(\ldots(f(0)) \ldots) - 1}{n + 1 f^{\mathrm{s}}}\]
|
There are three families.
- \(f(x) = x + 1\) .
- \(f(x) = x(x - 1)g(x) + 1\) for any polynomial \(g(x)\) (i.e., any \(f(x)\) such that \(f(0) = f(1) = 1\) ).
- \(f(x) = x(x - 1)(x + 1)g(x) + (2x^2 - 1)\) for any polynomial \(g(x)\) (i.e., any \(f(x)\) such that \(f(0) = -1\) , \(f(-1) = f(1) = 1\) ).
These all clearly work, so we focus on proving that these are all solutions.
Claim — For any prime \(p\) , either
(a) \(f(1) \equiv 1\) (mod \(p\) ) or
(b) the directed graph of \(f\) in \(\mathbb{F}_p\) forms a single cycle of size \(p\) .
Proof. Work modulo \(p\) . Consider the sequence
\[0,f(0),f(f(0)),\ldots ,\]
which must be eventually periodic. Clearly 1 must be in the periodic part by taking \(n\) to be a large multiple of \(p\) . Now, note that since the non- periodic part must have size less than \(p\) , we have
\[\left. \begin{array}{l}{f^{p + 1}(0) = 1}\\ {f^{2p + 1}(0) = 1} \end{array} \right\} \Longrightarrow f^{p}(1) = 1,\]
so the period must divide \(p\) and hence must be either 1 or \(p\) . If it is 1, then \(f(1) = 1\) . Otherwise, (b) holds. \(\square\)
Next, we note that if \(f(x) - x\) is non- constant, then by Schur's theorem on \(f(x) - x\) , \(f\) has a fixed point modulo infinitely many primes \(p\) , so (b) fails for infinitely many primes \(p\) . This means that (a) holds for infinitely many primes \(p\) , so \(f(1) = 1\) . Therefore, either \(f(x) - x\) is constant or \(f(1) = 1\) .
In the case that \(f(x) - x\) a constant \(c\) , \(f^{n + 1}(0) - 1 = (n + 1)c - 1\) , so \(n \mid c - 1\) for all \(n\) and \(f(x) = x + 1\) . Henceforth, assume \(f(1) = 1\) .
Since \(f(0) \mid f^k (0)\) for all \(k\) , plugging in \(n = |f(0)|\) gives
\[f(0) \mid f^{|f(0)| + 1}(0) - 1 \Longrightarrow f(0) \mid 1 \Longrightarrow f(0) = \pm 1.\]
If \(f(0) = 1\) , then we are done. Otherwise, assume \(f(0) = - 1\) . Then, \(f(- 1)\) is odd because \(f(1) = 1\) , so plugging in \(n = |f(- 1)| = 2k - 1\) gives
\[f(-1) \mid f^{2k}(0) - 1.\]
We have that \(f^2 (0) = 0\) modulo \(f(- 1) = f^2 (0)\) , so \(f(- 1) \mid 1\) . This gives \(f(- 1) = \pm 1\) . If \(f(- 1) = - 1\) , then we have \(f^n (0) = - 1\) for all \(n \geq 3\) , which makes the divisibility condition fail. Hence, \(f(- 1) = 1\) , and we get the third solution set.
Remark (author). An easier variant is to ask for all polynomials \(f\) with integer coefficients such that \(n \mid f^n (0)\) for all positive integers \(n\) .
|
proof
|
Incomplete
|
Yes
|
math-word-problem
|
Number Theory
|
Find all polynomials \(f\) with integer coefficients such that for all positive integers \(n\) ,
\[n \text{ divides } \frac{f(f(\ldots(f(0)) \ldots) - 1}{n + 1 f^{\mathrm{s}}}\]
|
There are three families.
- \(f(x) = x + 1\) .
- \(f(x) = x(x - 1)g(x) + 1\) for any polynomial \(g(x)\) (i.e., any \(f(x)\) such that \(f(0) = f(1) = 1\) ).
- \(f(x) = x(x - 1)(x + 1)g(x) + (2x^2 - 1)\) for any polynomial \(g(x)\) (i.e., any \(f(x)\) such that \(f(0) = -1\) , \(f(-1) = f(1) = 1\) ).
These all clearly work, so we focus on proving that these are all solutions.
Claim — For any prime \(p\) , either
(a) \(f(1) \equiv 1\) (mod \(p\) ) or
(b) the directed graph of \(f\) in \(\mathbb{F}_p\) forms a single cycle of size \(p\) .
Proof. Work modulo \(p\) . Consider the sequence
\[0,f(0),f(f(0)),\ldots ,\]
which must be eventually periodic. Clearly 1 must be in the periodic part by taking \(n\) to be a large multiple of \(p\) . Now, note that since the non- periodic part must have size less than \(p\) , we have
\[\left. \begin{array}{l}{f^{p + 1}(0) = 1}\\ {f^{2p + 1}(0) = 1} \end{array} \right\} \Longrightarrow f^{p}(1) = 1,\]
so the period must divide \(p\) and hence must be either 1 or \(p\) . If it is 1, then \(f(1) = 1\) . Otherwise, (b) holds. \(\square\)
Next, we note that if \(f(x) - x\) is non- constant, then by Schur's theorem on \(f(x) - x\) , \(f\) has a fixed point modulo infinitely many primes \(p\) , so (b) fails for infinitely many primes \(p\) . This means that (a) holds for infinitely many primes \(p\) , so \(f(1) = 1\) . Therefore, either \(f(x) - x\) is constant or \(f(1) = 1\) .
In the case that \(f(x) - x\) a constant \(c\) , \(f^{n + 1}(0) - 1 = (n + 1)c - 1\) , so \(n \mid c - 1\) for all \(n\) and \(f(x) = x + 1\) . Henceforth, assume \(f(1) = 1\) .
Since \(f(0) \mid f^k (0)\) for all \(k\) , plugging in \(n = |f(0)|\) gives
\[f(0) \mid f^{|f(0)| + 1}(0) - 1 \Longrightarrow f(0) \mid 1 \Longrightarrow f(0) = \pm 1.\]
If \(f(0) = 1\) , then we are done. Otherwise, assume \(f(0) = - 1\) . Then, \(f(- 1)\) is odd because \(f(1) = 1\) , so plugging in \(n = |f(- 1)| = 2k - 1\) gives
\[f(-1) \mid f^{2k}(0) - 1.\]
We have that \(f^2 (0) = 0\) modulo \(f(- 1) = f^2 (0)\) , so \(f(- 1) \mid 1\) . This gives \(f(- 1) = \pm 1\) . If \(f(- 1) = - 1\) , then we have \(f^n (0) = - 1\) for all \(n \geq 3\) , which makes the divisibility condition fail. Hence, \(f(- 1) = 1\) , and we get the third solution set.
Remark (author). An easier variant is to ask for all polynomials \(f\) with integer coefficients such that \(n \mid f^n (0)\) for all positive integers \(n\) .
|
{
"exam": "IMO",
"problem_label": "8",
"problem_match": "Problem 8. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 3.2\\) Solution to TSTST 8, by Pitchayut Saengrungkonga \n",
"tier": "T0",
"year": "2025"
}
|
Let acute triangle \(ABC\) have orthocenter \(H\) . Let \(B_{1}\) , \(C_{1}\) , \(B_{2}\) , and \(C_{2}\) be collinear points which lie on lines \(AB\) , \(AC\) , \(BH\) , and \(CH\) , respectively. Let \(\omega_{B}\) and \(\omega_{C}\) be the circumcircles of triangles \(BB_{1}B_{2}\) and \(CC_{1}C_{2}\) , respectively. Prove that the radical axis of \(\omega_{B}\) and \(\omega_{C}\) intersects the line through their centers on the nine- point circle of triangle \(ABC\) .
|
\(\P\) Solution (author) The first important step is to introduce \(N\) , the circumcenter of \(H B_{2}C_{2}\) .
Claim — Lines \(N B_{2}\) and \(N C_{2}\) are tangent to \((B B_{1}B_{2})\) and \((C C_{1}C_{2})\) , respectively.
Proof. This follows from chasing
\[\angle N B_{2}B = \angle N B_{2}H = 90^{\circ} - \angle H C_{2}B_{2} = \angle B_{2}B_{1}B.\]
An analogous proof works for the other side.
Since \(N B_{2} = N C_{2}\) , it follows that \(N\) lies on the radical axis of \((B B_{1}B_{2})\) and \((C C_{1}C_{2})\) . Thus we want to show \(X\) , the foot of \(N\) onto \(O_{B}O_{C}\) , lies on the nine- point circle.

Let \(D\) , \(E\) , \(F\) be the feet of the altitudes in \(\triangle A B C\) , and let \(M_{B}\) , \(M_{C}\) be the midpoints of \(B H\) , \(C H\) . Let \(B_{3}\) , \(C_{3}\) be the second intersections of \((B_{2}C_{2}H)\) with \((B B_{1}B_{2})\) , \((C C_{1}C_{2})\) .
Claim — Hexagons \(O_{B}B_{2}B_{3}M_{B}X N\) and \(O_{C}C_{2}C_{3}M_{C}X N\) are cyclic.
Proof. Clearly \(B_{2}\) , \(B_{3}\) and \(X\) lie on the circle of diameter \(O_{B}N\) . To show \(M_{B}\) lies in this circle, we first note that \(BB_{3}HFD\) is cyclic. Indeed, this follows from chasing
\[\angle BB_{3}H = \angle B_{2}B_{3}H - \angle B_{2}B_{3}B = \angle B_{2}C_{2}H - \angle B_{2}B_{1}B = \angle B_{1}FC_{2} = \angle BFF.\]
This circle has center \(M_{B}\) , so \(O_{B}M_{B}\) and \(M_{B}N\) are the perpendicular bisectors of \(BB_{3}\) , \(B_{3}H\) . Since \(BB_{3} \perp B_{3}H\) , \(O_{B}M_{B} \perp M_{B}N\) , as we wanted to show. \(\square\)
Now we are ready to finish. We know \(\angle M_{B}DM_{C} = \angle M_{C}HM_{B} = \angle BAC\) . We will now show that \(\angle M_{B}XM_{C}\) gives the same value. On one hand
\[\angle M_{B}XO_{B} = \angle M_{B}B_{2}O_{B} = \angle BB_{2}O_{B} = 90^{\circ} - \angle B_{2}B_{1}B = 90^{\circ} - \angle C_{1}B_{1}A.\]
Similarly \(\angle O_{C}XM_{C} = 90^{\circ} - \angle AC_{1}B_{1}\) , so
\[\angle M_{B}XM_{C} = (90^{\circ} - \angle C_{1}B_{1}A) + (90^{\circ} - \angle AC_{1}B_{1}) = \angle BAC,\]
which establishes the result.
Remark (author). Since the problem is symmetric under \(A \leftrightarrow H\) , a similar solution can be found by considering the circumcenter of \(\triangle AB_{1}C_{1}\) (instead of \(N\) ). Moreover, introducing both circumcenters adds more structure to the diagram, which can make it easier to finish.
The most important step in this solution is to introduce the point \(N\) . This can be motivated by noticing that the circles \((BB_{1}B_{2})\) and \((HB_{2}C_{2})\) are orthogonal.
Moving Points Solution (Krishna) Let \(E, F\) be the feet of the \(B, C\) altitudes, as in the first solution.
Claim — As \(\ell\) varies while staying parallel to a fixed line, \(\overline{O_{B}O_{C}}\) passes through a fixed point \(Y\) on the nine- point circle.
Proof. Move \(\ell\) linearly. Then \(\triangle BB_{1}B_{2}\) is dilating at \(B\) linearly, so \(O_{B}\) moves linearly. Similarly \(O_{C}\) moves linearly. Furthermore, we have that
\[\angle \overline{B O_{B}} = 90 + \angle B A + \angle B H - \angle \ell = \angle B A + \angle B C - \angle \ell ,\]
which by symmetry means \(\overline{B O_{B}} \parallel \overline{C O_{C}}\) . Thus we need to find a point \(Y\) on the nine- point circle such that \(O_{B} - O_{C} - Y\) in 2 cases.

Suppose \(\ell\) passes through \(H\) . In that case, let \(Q = (BB_{1}H)\cap (CC_{1}H)\) . We get that \(Q\) lies on \((ABC)\) by chasing
\[\angle BQC = \angle BQH + \angle HQC = \angle BB_{1}H + \angle HC_{1}C = \angle ABB_{1} + \angle BC_{1}A = \angle BAC.\]
The perpendicular bisector of \(\overline{HQ}\) is \(\overline{O_{B}O_{C}}\) , and the midpoint of \(HQ\) lies on the nine- point circle. Let the perpendicular from \(Q\) to \(\overline{HQ}\) intersect \((ABC)\) at \(Y_{1}\) . Then
\[\angle BAY_{1} = \angle BQY_{1} = 90 + \angle BQH = 90 + \angle AB_{1}H,\]
so \(\overline{AY_{1}}\perp \ell\) . If \(Y\) is the midpoint of \(HY_{1}\) , then \(Y\) lies on \(\overline{O_{B}O_{C}}\) and the nine- point circle of \((ABC)\) . The line between \(Y\) and the midpoint of \(AH\) is perpendicular to \(\ell\) . Hence when \(\ell\) passes through \(A\) , by symmetry we also get \(O_{B} - O_{C} - Y\) , as desired (this angle chase is basically done as part of 2019 TSTST 5). \(\square\)
Let \(P_{\infty}\) be the point at infinity of \(\ell\) , and let \(P = r\cap \ell\) . Since \(PB_{1}\cdot PB_{2} = PC_{1}\cdot PC_{2}\) (with signed lengths), we have that \((P,P_{\infty}),(B_{1},B_{2}),(C_{1},C_{2})\) are 3 pairs under the same involution on \(\ell\) . Then by DIT on the 4 points \(A,H,E,F\) and the line \(\ell\) , if \(\mathcal{C}\) is the conic through \(A,H,E,F,P_{\infty}\) , then \(P\) also lies on \(\mathcal{C}\) . Now we do moving points.

- Let \(P_{\infty}\) be a sufficiently general fixed point at infinity (proving the problem for sufficiently general \(P_{\infty}\) suffices by continuity.
- Define \(P\) as a moving point with degree 2 varying on the conic through \(A, H, E, F, P_{\infty}\) .
- As we let \(P\) vary and we let \(\ell = \overline{PP_{\infty}}\) , we get that \(\overline{PP_{\infty}}\) has degree 1 so \(B_{1}\) has degree 1. The perpendicular bisector of \(BB_{1}\) then has degree 1, and \(\overline{BO_{B}}\) is fixed so \(O_{B}\) has degree 1.
- \(Y\) has degree 0, and the antipode \(Y'\) of \(Y\) on the nine-point circle has degree 0. It suffices to show that \(\overline{Y'P} \perp \overline{OBY}\) .
- \(\overline{Y'P}\) has degree \(\leq 2\) and \(\overline{OBY}\) has degree 1, so we get a degree 3 statement that needs to be checked at 4 cases.
We can do \(P = A, H, E, F\) . \(P = H\) and \(P = A\) are true by previous work. By symmetry, to solve \(P = E\) and \(P = F\) we only need to look at \(P = E\) . In this case, we want to show that \(E - OB = OC\) .
\[\angle EOB = \angle BA + \angle \ell -\angle BH = 90 + \angle CH + \angle \ell -90 - \angle AC = 90 - 90 + \angle EOC = \angle EOC,\]
as desired.
\(\P\) Solution (Vivian Loh) Let \(S_{B} = (BH) \cap (BB_{1}B_{2})\) , and \(S_{C} = (CH) \cap (CC_{1}C_{2})\) . Then \(S_{B}\) and \(S_{C}\) are the Miquel points of complete quadrilaterals \(\{B, B_{1}, B_{2}, H, C_{2}, CH \cap AB\}\) and \(\{C, C_{1}, C_{2}, H, B_{2}, BH \cap AC\}\) respectively, so \(S_{B}\) and \(S_{C}\) both lie on \((HB_{2}C_{2})\) . Furthermore, by radical center, \(P = B_{2}S_{B} \cap C_{2}S_{C}\) lies on the radical axis of \(\omega_{B}\) , \(\omega_{C}\) . Also note that if \(H'\) is the antipode of \(H\) with respect to \((HB_{2}C_{2})\) , then \(S_{B}\) and \(S_{C}\) are the projections of \(H\) onto \(BH'\) and \(CH'\) , respectively. Note that the 6 points \(H, B_{2}, C_{2}, H', S_{B}, S_{C}\) all lie on \((HH')\) .
Claim 3.1 — If \(O_{B}\) and \(O_{C}\) are the centers of \(\omega_{B}\) and \(\omega_{C}\) respectively, then \(O_{B}\) is the intersection of tangents to \((HH^{\prime})\) at \(B_{2}\) and \(S_{B}\) , while \(O_{C}\) is the intersection of tangents to \((HH^{\prime})\) at \(C_{2}\) and \(S_{C}\) .
Proof. Angle chasing; \(\angle B_{2}O_{B}S_{B} = 2\angle B_{2}BS_{B} = 2(90^{\circ} - \angle BHS_{B}) = 180^{\circ} - 2\angle BHS_{B}\) . It works for \(O_{C}\) similarly. \(\square\)
Claim 3.2 — \(O_{B}O_{C}\) is the polar of \(P\) with respect to \((HH^{\prime})\) .
Proof. By the definition of poles and polars, \(B_{2}S_{B}\) is the polar of \(O_{B}\) and \(C_{2}S_{C}\) is the polar of \(O_{C}\) , and by La Hire's, we know that a point lies on the polar of \(O_{B}\) and the polar of \(O_{C}\) if and only if \(O_{B}\) and \(O_{C}\) both lie on its polar, so \(O_{B}O_{C}\) is the polar of \(B_{2}S_{B} \cap C_{2}S_{C} = P\) . \(\square\)
Since \(P\) lies on the radical axis of \(\omega_{B}\) and \(\omega_{C}\) , the desired point in the problem (the intersection of the radical axis and \(O_{B}O_{C}\) ) is the foot from \(P\) to \(O_{B}O_{C}\) , which is the inverse \(P^{*}\) of \(P\) about \((HH^{\prime})\) . It suffices to show that this point lies on the nine- point circle of \(\triangle ABC\) .
Let \(M_{B}\) and \(M_{C}\) be the midpoints of \(HB\) and \(HC\) . Then the nine- point circle of \(\triangle ABC\) passes through \(M_{B}\) , \(M_{C}\) , and the foot from \(H\) to \(BC\) , so \(P^{*}\) lies on this nine- point circle if and only if \(\angle M_{B}P^{*}M_{C} = \angle BHC\) .
Claim 3.3 — \(M_{B}^{*} \in B_{2}S_{B}\) , \(M_{C}^{*} \in C_{2}S_{C}\) .
Proof. This is simply angle chasing. We will show that \(M_{C}^{*} \in C_{2}S_{C}\) . Let \(O\) be the center of \((HH^{\prime})\) . Then \(\angle O M_{C}H = \angle O H M_{C}^{*}\) , which equals \(\angle O S_{C}M_{C}^{*}\) since \(O M_{C} \perp H S_{C}\) . However, \(\angle O S_{C}C_{2} = \angle H S_{C}C_{2} - \angle H S_{C}O = \angle (H C_{2}, S_{C}H^{\prime}) = \angle O M_{C}H\) , so \(M_{C}^{*} \in C_{2}S_{C}\) , and \(M_{B}^{*}\) follows similarly. \(\square\)
The last part is just angle chasing. We know from before that it is sufficient to show \(\angle M_{B}P^{*}M_{C} = \angle BHC\) . We have: \(\angle M_{B}P^{*}M_{C} = \angle OP^{*}M_{B} + \angle OP^{*}M_{C} = \angle OM_{B}^{*}P + \angle OM_{C}^{*}P = 360^{\circ} - \angle M_{B}^{*}OM_{C}^{*} - \angle M_{B}^{*}PM_{C}^{*} = 360^{\circ} - \angle S_{C}PS_{B} - \angle S_{C}H^{\prime}S_{B} = \angle H^{\prime}S_{B}P + \angle H^{\prime}S_{C}P = \angle B_{2}HC_{2} = \angle BHC\) , as desired.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let acute triangle \(ABC\) have orthocenter \(H\) . Let \(B_{1}\) , \(C_{1}\) , \(B_{2}\) , and \(C_{2}\) be collinear points which lie on lines \(AB\) , \(AC\) , \(BH\) , and \(CH\) , respectively. Let \(\omega_{B}\) and \(\omega_{C}\) be the circumcircles of triangles \(BB_{1}B_{2}\) and \(CC_{1}C_{2}\) , respectively. Prove that the radical axis of \(\omega_{B}\) and \(\omega_{C}\) intersects the line through their centers on the nine- point circle of triangle \(ABC\) .
|
\(\P\) Solution (author) The first important step is to introduce \(N\) , the circumcenter of \(H B_{2}C_{2}\) .
Claim — Lines \(N B_{2}\) and \(N C_{2}\) are tangent to \((B B_{1}B_{2})\) and \((C C_{1}C_{2})\) , respectively.
Proof. This follows from chasing
\[\angle N B_{2}B = \angle N B_{2}H = 90^{\circ} - \angle H C_{2}B_{2} = \angle B_{2}B_{1}B.\]
An analogous proof works for the other side.
Since \(N B_{2} = N C_{2}\) , it follows that \(N\) lies on the radical axis of \((B B_{1}B_{2})\) and \((C C_{1}C_{2})\) . Thus we want to show \(X\) , the foot of \(N\) onto \(O_{B}O_{C}\) , lies on the nine- point circle.

Let \(D\) , \(E\) , \(F\) be the feet of the altitudes in \(\triangle A B C\) , and let \(M_{B}\) , \(M_{C}\) be the midpoints of \(B H\) , \(C H\) . Let \(B_{3}\) , \(C_{3}\) be the second intersections of \((B_{2}C_{2}H)\) with \((B B_{1}B_{2})\) , \((C C_{1}C_{2})\) .
Claim — Hexagons \(O_{B}B_{2}B_{3}M_{B}X N\) and \(O_{C}C_{2}C_{3}M_{C}X N\) are cyclic.
Proof. Clearly \(B_{2}\) , \(B_{3}\) and \(X\) lie on the circle of diameter \(O_{B}N\) . To show \(M_{B}\) lies in this circle, we first note that \(BB_{3}HFD\) is cyclic. Indeed, this follows from chasing
\[\angle BB_{3}H = \angle B_{2}B_{3}H - \angle B_{2}B_{3}B = \angle B_{2}C_{2}H - \angle B_{2}B_{1}B = \angle B_{1}FC_{2} = \angle BFF.\]
This circle has center \(M_{B}\) , so \(O_{B}M_{B}\) and \(M_{B}N\) are the perpendicular bisectors of \(BB_{3}\) , \(B_{3}H\) . Since \(BB_{3} \perp B_{3}H\) , \(O_{B}M_{B} \perp M_{B}N\) , as we wanted to show. \(\square\)
Now we are ready to finish. We know \(\angle M_{B}DM_{C} = \angle M_{C}HM_{B} = \angle BAC\) . We will now show that \(\angle M_{B}XM_{C}\) gives the same value. On one hand
\[\angle M_{B}XO_{B} = \angle M_{B}B_{2}O_{B} = \angle BB_{2}O_{B} = 90^{\circ} - \angle B_{2}B_{1}B = 90^{\circ} - \angle C_{1}B_{1}A.\]
Similarly \(\angle O_{C}XM_{C} = 90^{\circ} - \angle AC_{1}B_{1}\) , so
\[\angle M_{B}XM_{C} = (90^{\circ} - \angle C_{1}B_{1}A) + (90^{\circ} - \angle AC_{1}B_{1}) = \angle BAC,\]
which establishes the result.
Remark (author). Since the problem is symmetric under \(A \leftrightarrow H\) , a similar solution can be found by considering the circumcenter of \(\triangle AB_{1}C_{1}\) (instead of \(N\) ). Moreover, introducing both circumcenters adds more structure to the diagram, which can make it easier to finish.
The most important step in this solution is to introduce the point \(N\) . This can be motivated by noticing that the circles \((BB_{1}B_{2})\) and \((HB_{2}C_{2})\) are orthogonal.
Moving Points Solution (Krishna) Let \(E, F\) be the feet of the \(B, C\) altitudes, as in the first solution.
Claim — As \(\ell\) varies while staying parallel to a fixed line, \(\overline{O_{B}O_{C}}\) passes through a fixed point \(Y\) on the nine- point circle.
Proof. Move \(\ell\) linearly. Then \(\triangle BB_{1}B_{2}\) is dilating at \(B\) linearly, so \(O_{B}\) moves linearly. Similarly \(O_{C}\) moves linearly. Furthermore, we have that
\[\angle \overline{B O_{B}} = 90 + \angle B A + \angle B H - \angle \ell = \angle B A + \angle B C - \angle \ell ,\]
which by symmetry means \(\overline{B O_{B}} \parallel \overline{C O_{C}}\) . Thus we need to find a point \(Y\) on the nine- point circle such that \(O_{B} - O_{C} - Y\) in 2 cases.

Suppose \(\ell\) passes through \(H\) . In that case, let \(Q = (BB_{1}H)\cap (CC_{1}H)\) . We get that \(Q\) lies on \((ABC)\) by chasing
\[\angle BQC = \angle BQH + \angle HQC = \angle BB_{1}H + \angle HC_{1}C = \angle ABB_{1} + \angle BC_{1}A = \angle BAC.\]
The perpendicular bisector of \(\overline{HQ}\) is \(\overline{O_{B}O_{C}}\) , and the midpoint of \(HQ\) lies on the nine- point circle. Let the perpendicular from \(Q\) to \(\overline{HQ}\) intersect \((ABC)\) at \(Y_{1}\) . Then
\[\angle BAY_{1} = \angle BQY_{1} = 90 + \angle BQH = 90 + \angle AB_{1}H,\]
so \(\overline{AY_{1}}\perp \ell\) . If \(Y\) is the midpoint of \(HY_{1}\) , then \(Y\) lies on \(\overline{O_{B}O_{C}}\) and the nine- point circle of \((ABC)\) . The line between \(Y\) and the midpoint of \(AH\) is perpendicular to \(\ell\) . Hence when \(\ell\) passes through \(A\) , by symmetry we also get \(O_{B} - O_{C} - Y\) , as desired (this angle chase is basically done as part of 2019 TSTST 5). \(\square\)
Let \(P_{\infty}\) be the point at infinity of \(\ell\) , and let \(P = r\cap \ell\) . Since \(PB_{1}\cdot PB_{2} = PC_{1}\cdot PC_{2}\) (with signed lengths), we have that \((P,P_{\infty}),(B_{1},B_{2}),(C_{1},C_{2})\) are 3 pairs under the same involution on \(\ell\) . Then by DIT on the 4 points \(A,H,E,F\) and the line \(\ell\) , if \(\mathcal{C}\) is the conic through \(A,H,E,F,P_{\infty}\) , then \(P\) also lies on \(\mathcal{C}\) . Now we do moving points.

- Let \(P_{\infty}\) be a sufficiently general fixed point at infinity (proving the problem for sufficiently general \(P_{\infty}\) suffices by continuity.
- Define \(P\) as a moving point with degree 2 varying on the conic through \(A, H, E, F, P_{\infty}\) .
- As we let \(P\) vary and we let \(\ell = \overline{PP_{\infty}}\) , we get that \(\overline{PP_{\infty}}\) has degree 1 so \(B_{1}\) has degree 1. The perpendicular bisector of \(BB_{1}\) then has degree 1, and \(\overline{BO_{B}}\) is fixed so \(O_{B}\) has degree 1.
- \(Y\) has degree 0, and the antipode \(Y'\) of \(Y\) on the nine-point circle has degree 0. It suffices to show that \(\overline{Y'P} \perp \overline{OBY}\) .
- \(\overline{Y'P}\) has degree \(\leq 2\) and \(\overline{OBY}\) has degree 1, so we get a degree 3 statement that needs to be checked at 4 cases.
We can do \(P = A, H, E, F\) . \(P = H\) and \(P = A\) are true by previous work. By symmetry, to solve \(P = E\) and \(P = F\) we only need to look at \(P = E\) . In this case, we want to show that \(E - OB = OC\) .
\[\angle EOB = \angle BA + \angle \ell -\angle BH = 90 + \angle CH + \angle \ell -90 - \angle AC = 90 - 90 + \angle EOC = \angle EOC,\]
as desired.
\(\P\) Solution (Vivian Loh) Let \(S_{B} = (BH) \cap (BB_{1}B_{2})\) , and \(S_{C} = (CH) \cap (CC_{1}C_{2})\) . Then \(S_{B}\) and \(S_{C}\) are the Miquel points of complete quadrilaterals \(\{B, B_{1}, B_{2}, H, C_{2}, CH \cap AB\}\) and \(\{C, C_{1}, C_{2}, H, B_{2}, BH \cap AC\}\) respectively, so \(S_{B}\) and \(S_{C}\) both lie on \((HB_{2}C_{2})\) . Furthermore, by radical center, \(P = B_{2}S_{B} \cap C_{2}S_{C}\) lies on the radical axis of \(\omega_{B}\) , \(\omega_{C}\) . Also note that if \(H'\) is the antipode of \(H\) with respect to \((HB_{2}C_{2})\) , then \(S_{B}\) and \(S_{C}\) are the projections of \(H\) onto \(BH'\) and \(CH'\) , respectively. Note that the 6 points \(H, B_{2}, C_{2}, H', S_{B}, S_{C}\) all lie on \((HH')\) .
Claim 3.1 — If \(O_{B}\) and \(O_{C}\) are the centers of \(\omega_{B}\) and \(\omega_{C}\) respectively, then \(O_{B}\) is the intersection of tangents to \((HH^{\prime})\) at \(B_{2}\) and \(S_{B}\) , while \(O_{C}\) is the intersection of tangents to \((HH^{\prime})\) at \(C_{2}\) and \(S_{C}\) .
Proof. Angle chasing; \(\angle B_{2}O_{B}S_{B} = 2\angle B_{2}BS_{B} = 2(90^{\circ} - \angle BHS_{B}) = 180^{\circ} - 2\angle BHS_{B}\) . It works for \(O_{C}\) similarly. \(\square\)
Claim 3.2 — \(O_{B}O_{C}\) is the polar of \(P\) with respect to \((HH^{\prime})\) .
Proof. By the definition of poles and polars, \(B_{2}S_{B}\) is the polar of \(O_{B}\) and \(C_{2}S_{C}\) is the polar of \(O_{C}\) , and by La Hire's, we know that a point lies on the polar of \(O_{B}\) and the polar of \(O_{C}\) if and only if \(O_{B}\) and \(O_{C}\) both lie on its polar, so \(O_{B}O_{C}\) is the polar of \(B_{2}S_{B} \cap C_{2}S_{C} = P\) . \(\square\)
Since \(P\) lies on the radical axis of \(\omega_{B}\) and \(\omega_{C}\) , the desired point in the problem (the intersection of the radical axis and \(O_{B}O_{C}\) ) is the foot from \(P\) to \(O_{B}O_{C}\) , which is the inverse \(P^{*}\) of \(P\) about \((HH^{\prime})\) . It suffices to show that this point lies on the nine- point circle of \(\triangle ABC\) .
Let \(M_{B}\) and \(M_{C}\) be the midpoints of \(HB\) and \(HC\) . Then the nine- point circle of \(\triangle ABC\) passes through \(M_{B}\) , \(M_{C}\) , and the foot from \(H\) to \(BC\) , so \(P^{*}\) lies on this nine- point circle if and only if \(\angle M_{B}P^{*}M_{C} = \angle BHC\) .
Claim 3.3 — \(M_{B}^{*} \in B_{2}S_{B}\) , \(M_{C}^{*} \in C_{2}S_{C}\) .
Proof. This is simply angle chasing. We will show that \(M_{C}^{*} \in C_{2}S_{C}\) . Let \(O\) be the center of \((HH^{\prime})\) . Then \(\angle O M_{C}H = \angle O H M_{C}^{*}\) , which equals \(\angle O S_{C}M_{C}^{*}\) since \(O M_{C} \perp H S_{C}\) . However, \(\angle O S_{C}C_{2} = \angle H S_{C}C_{2} - \angle H S_{C}O = \angle (H C_{2}, S_{C}H^{\prime}) = \angle O M_{C}H\) , so \(M_{C}^{*} \in C_{2}S_{C}\) , and \(M_{B}^{*}\) follows similarly. \(\square\)
The last part is just angle chasing. We know from before that it is sufficient to show \(\angle M_{B}P^{*}M_{C} = \angle BHC\) . We have: \(\angle M_{B}P^{*}M_{C} = \angle OP^{*}M_{B} + \angle OP^{*}M_{C} = \angle OM_{B}^{*}P + \angle OM_{C}^{*}P = 360^{\circ} - \angle M_{B}^{*}OM_{C}^{*} - \angle M_{B}^{*}PM_{C}^{*} = 360^{\circ} - \angle S_{C}PS_{B} - \angle S_{C}H^{\prime}S_{B} = \angle H^{\prime}S_{B}P + \angle H^{\prime}S_{C}P = \angle B_{2}HC_{2} = \angle BHC\) , as desired.
|
{
"exam": "IMO",
"problem_label": "9",
"problem_match": "Problem 9. ",
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2025.jsonl",
"solution_match": "## \\(\\S 3.3\\) Solution to TSTST 9, by Ruben Carpenter \n",
"tier": "T0",
"year": "2025"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.